Образовательный портал. Образование / Среднее образование и школа / Рис 111 найти среднюю линию трапеции авсд. Курсы егэ и огэ (гиа). Средние линии четырехугольника. Теорема Вариньона

Рис 111 найти среднюю линию трапеции авсд. Курсы егэ и огэ (гиа). Средние линии четырехугольника. Теорема Вариньона

17.04.2019

Цели урока:

1) познакомить учащихся с понятием средней линии трапеции, рассмотреть её свойства и доказать их;

2) научить строить среднюю линию трапеции;

3) развивать умение учащихся использовать определение средней линии трапеции и свойства средней линии трапеции при решении задач;

4) продолжать формировать у учащихся умение говорить грамотно, используя необходимые математические термины; доказывать свою точку зрения;

Использование, распространение или воспроизведение на других форумах разрешено при условии, что автор оригинала или лицензиар зачислен, и что оригинальная публикация в этом журнале цитируется в соответствии с принятой академической практикой. Запрещается использование, распространение или воспроизведение, которое не соответствует этим условиям. Связанные с Эймсом исследования, перечисленные выше, потребовали, чтобы наблюдатели указывали на любые развороты движения, воспринимаемые при непрерывном вращении трапецеидальной фигуры.

Средние линии четырехугольника. Теорема Вариньона

Затем фактор интереса обрабатывался, чтобы определить, оказало ли оно существенное влияние на число или частоту обращений. Такие манипуляции с перспективой, параллакс движения, яркость, затенение, интерпозиция и кажущаяся ориентация имели такой эффект, в то время как внутренняя текстура и окончание границы фигуры не выполнялись.

5) развивать логическое мышление, память, внимание.

Ход урока

1. Проверка домашнего задания происходит в течение урока. Домашнее задание было устным, вспомнить:

а) определение трапеции; виды трапеций;

б) определение средней линии треугольника;

в) свойство средней линии треугольника;

г) признак средней линии треугольника.

Трапеция, вращающаяся на 360 °, состоит из последовательности изображений; изображения меняются систематически и со скоростью, определяемой экспериментатором. Эта траектория изображения включает в себя несколько сложных процессов, включая усталость и импульс объекта. Усталость относится к тенденции двусмысленных фигур, чтобы вызвать чередование возможных восприятий, по-видимому, потому, что нейроны, генерирующие активное восприятие, становятся «усталыми», позволяя альтернативному восприятию стать активным.

Импульс объекта относится к тенденции, в краткосрочной перспективе, продолжать видеть один и тот же объект посредством изменения взглядов. Такой репрезентативный импульс во вращении имеет последствия для сообщаемого восприятия глубины, когда вращающаяся трапеция пересекает фронтально-параллельную плоскость. В этот момент, если ребро, которое идет вперед по глубине, продолжает двигаться вперед или наоборот, направление его глубины зависит от вращательного репрезентативного импульса, потому что объективная глубина мгновенно полностью неоднозначна.

2. Изучение нового материала.

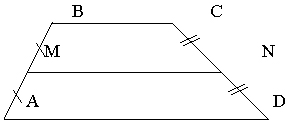
а) На доске изображена трапеция ABCD.

б) Учитель предлагает вспомнить определение трапеции. На каждой парте имеется схема-подсказка, помогающая вспомнить основные понятия в теме “Трапеция” (см. Приложение 1). Приложение 1 выдаётся на каждую парту.

Ученики изображают трапецию ABCD в тетради.

Таким образом, парадигма Эймса представляет собой, по сути, серию последовательных испытаний, которые происходят каждые 180 ° вращения, когда вращающаяся трапеция находится точно в фронто-параллельной плоскости. На этом этапе репрезентативный импульс ставится в конкуренцию со многими другими факторами, которые определяют изменение направления.

Хотя наша цель, в конечном счете, состоит в том, чтобы понять виртуозную трапециевидную иллюзию, учитывая нынешнюю технологию, ситуация с виндсерфингом слишком сложна и слишком изучена. Трапеция Эймса является идеализированным упрощением и имеет то преимущество, что уже получила обширные полезные исследования. Однако даже вращающееся окно Эймса излишне усложняется, поскольку оно включает просмотр трапецоидов под всеми возможными углами и подразумеваемую последовательность последовательных испытаний, поскольку трапеция неоднократно проходит через переднюю параллельную плоскость.

в) Учитель предлагает вспомнить, в какой теме встречалось понятие средней линии (“Средняя линия треугольника”). Учащиеся вспоминают определение средней линии треугольника и её свойство.

д) Записывают определение средней линии трапеции, изображая её в тетради.

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

Чтобы еще больше упростить и сосредоточить внимание на изучении трапециевидных иллюзий, мы рассматриваем только одну типичную ориентацию Эймепоподобной трапеции. Зависимая переменная - какая сторона трапеции находится ближе к наблюдателю. Восприятие глубины в трапеции значительно усиливается, как в окне Эймса, вращая его, в этом случае вращая трапецию назад и вперед вокруг своей первоначальной ориентации. Такое вращение обычно создает яркое восприятие глубины в момент восприятия трапеции. Третий фактор - это контроль точки фиксации.

Наше решение состоит в том, чтобы показать две вращающиеся трапеции с наблюдателем, визуально зафиксированным в точке фиксации между ними. Наблюдателям были представлены дисплеи, содержащие трапециевидные контуры, в которых местоположение оси вращения для конкретного испытания было выбрано случайным образом из пяти одинаково разнесенных мест, от совпадающего с короткой стороной до совпадающей с длинной стороной.

Свойство средней линии трапеции на данном этапе остаётся не доказанным, поэтому следующий этап урока предполагает работу над доказательством свойства средней линии трапеции.

Теорема. Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Дисплей стимула состоял из белых контуров двух трапециевидных фигур и центральной белой точки фиксации на черном фоне. Стимулы смотрели в темной комнате. Длинная сторона трапеции составляла 43 ° визуального угла, короткая сторона - 22 ° визуального угла, а максимальное расстояние между двумя параллельными сторонами трапеции составляло 43 ° визуального угла. Длины длинных и коротких сторон не изменялись во время вращения, и они оставались постоянными во время экспериментов. Расстояние от центра одной трапеции до центра другого составляло 86 ° визуального угла.

Дано: ABCD – трапеция,

MN – средняя линия ABCD

Доказать , что:

1. BC || MN || AD.

2. MN = (AD + BC).

Можно выписать некоторые следствия, вытекающие из условия теоремы:

AM = MB, CN = ND, BC || AD.

На основании только перечисленных свойств доказать требуемое невозможно. Система вопросов и упражнений должна подвести учащихся к желанию связать среднюю линию трапеции со средней линией какого-нибудь треугольника, свойства которой они уже знают. Если предложений не последует, то можно задать вопрос: как построить треугольник, для которого отрезок MN являлся бы средней линией?

Расстояние просмотра составляло 90 см, и наблюдатели рассматривали дисплей монокулярно своим предпочтительным глазом, сидя прямо. Дисплей виндсерфера состоит из двух трапеций, расположенных выше и один ниже точки фиксации, ориентированных вертикальными параллельными сторонами. Левосторонняя ориентация трапеций была выбрана случайным образом на каждом испытании - короткая сторона появилась с левой или с правой стороны дисплея с равной вероятностью. Таким образом, двумя возможными ориентациями стимула были.

Причиной отображения двух трапецеидов на каждом дисплее было то, чтобы точка фиксации была центрирована относительно длинной и короткой сторон фигур без добавления каких-либо внутренних элементов внутри трапеций. Наблюдатели рассматривали стимулы перемещения контуров трапеций на экране компьютера. Просмотр был монокуляр с предпочтительным глазом; другой глаз был покрыт глазным пластырем. На каждом испытании трапеция колеблется дважды на ± 20 ° относительно одной из пяти случайно выбранных осей вращения.

Запишем дополнительное построение для одного из случаев.

Проведём прямую BN, пересекающую продолжение стороны AD в точке K.

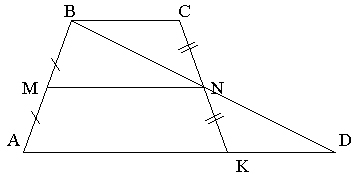
Появляется дополнительные элементы – треугольники: ABD, BNM, DNK, BCN. Если мы докажем, что BN = NK, то это будет означать, что MN – средняя линия ABD, а дальше можно будет воспользоваться свойством средней линии треугольника и доказать необходимое.

По завершении поворотного трапециевидного дисплея пустой экран появлялся до тех пор, пока наблюдатель не зарегистрировал свой ответ, и следующее испытание началось немедленно. Все суждения носили характер: «Какая сторона ближе к вам в глубину?» И были обозначены нажатиями клавиш. Возможные ответы были следующими.

Короткая сторона впереди на протяжении всего испытания, длинная сторона впереди на протяжении всего испытания, короткая сторона впереди в начале испытания, изменяющаяся хотя бы один раз во время испытания, длинная сторона впереди в начале испытания, изменяющаяся хотя бы один раз во время испытания фаза - две трапеции находятся в противоположных конфигурациях глубины и не имеют трехмерного восприятия. Связанное наблюдение во всех этих экспериментах состоит в том, что, когда наблюдатель воспринимает особый перцептивный режим, наблюдатель обычно не знает о возможности других режимов.

Доказательство:

1. Рассмотрим BNC и DNK, в них:

а) CNB =DNK (свойство вертикальных углов);

б) BCN = NDK (свойство внутренних накрест лежащих углов);

в) CN = ND (по следствию из условия теоремы).

Значит BNC =DNK (по стороне и двум прилежащим к ней углам).

Что и требовалось доказать.

Доказательство можно провести на уроке устно, а дома восстановить и записать в тетради (на усмотрение учителя).

Семь наблюдателей выполнили два блока по 200 испытаний каждый, в общей сложности 400 испытаний. Каждое условие имеет 40 наблюдений раз 7 наблюдателей. Несмотря на то, что наблюдателям были предоставлены шесть возможных ответов, изложенных в предыдущем разделе, 96% от общего числа ответов были «короткой стороной впереди на протяжении всего судебного разбирательства» или «длинной стороной впереди на протяжении всего судебного разбирательства». Это будет удобно, поэтому описывая данные и в последующем обсуждении, чтобы разделить ответы на две группы: Группа 1: короткие и длинные фронты; Группа 2: все другие ответы, т.е. категории ответов. 3.

Необходимо сказать и о других возможных способ доказательства этой теоремы:

1. Провести одну из диагоналей трапеции и использовать признак и свойство средней линии треугольника.

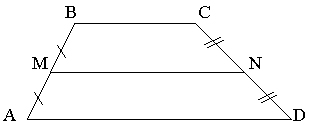
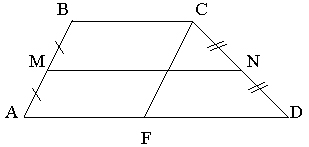
2. Провести CF || BA и рассмотреть параллелограмм ABCF и DCF.

Когда речь идет о пропорциях ответов в категориях 3-6, мы используем безусловные пропорции. Основными определяющими глубину реплики в эксперименте 1 были неявная трапециевидная перспектива и количество движения. В эксперименте 2 дисплеи идентичны, за исключением глобального поворота всего дисплея 90 против часовой стрелки. Поэтому те же факторы, что и в эксперименте 1, снова актуальны: неявная перспектива и количество движения.

Все аспекты стимулов были идентичны эксперименту 1, за исключением того, что весь дисплей повернут на 90 ° против часовой стрелки. Процедура в эксперименте 2 идентична процедуре в эксперименте. Семь наблюдателей Эксперимента 1 плюс один новый наблюдатель приняли участие в эксперименте.

3. Провести EF || BA и рассмотреть равенство FND и ENC.

ж) На этом этапе задаётся домашнее задание: п. 84, учебник под ред. Атанасяна Л.С. (доказательство свойства средней линии трапеции векторным способом), записать в тетради.

з) Решаем задачи на использование определения и свойства средней линии трапеции по готовым чертежам (см. Приложение 2). Приложение 2 выдаётся каждому учащемуся, и решение задач оформляется на этом же листе в краткой форме.

Трапецеидальная иллюзия отменена

Результаты эксперимента 3 обобщены на рис. 7. 7. Асимметрия ответов, типичная для конфигурации ВПП, как и в эксперименте 2, была сохранена в обоих условиях в текущем эксперименте, указывая на асимметрию восходящего восходящего движения на ВПП, переопределяя лево-правую симметрию конфигурация виндсерфера. Эффект ВПП несколько больше в координатах сетчатки, чем мировые координаты.

Изменение конфигурации сетчатки

Чтобы сравнить эффекты изменения конфигурации сетчатки и изменения конфигурации мира, необходимы перекрестные сравнения с данными из экспериментов 1 и 2. Для всех наблюдателей изменение конфигурации сетчатки от виндсерферов до ВПП параллельно с мировой конфигурацией виндсерфинга приводит к глубокому изменению структуры ответов, изменяя почти идеальную симметрию обратной трапецеидальной симметрии влево и вправо на высокосимметричную нижнюю сторону, смещение переднего отклика. Тем не менее, подразумеваемая интерпретация перспективы поддерживается так, что все наблюдатели значительно чаще сообщают о длинной стороне впереди, чем о короткой стороне.

Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

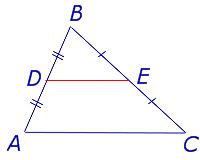
На рисунке 1 средней линией является отрезок DE .

Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

Эффект ВПП, который наблюдался в эксперименте 2, оставался сильным в эксперименте 3В. Однако, наклоняя голову на 90 ° в эксперименте 3В, изменяет ВПП на сетчатку в конфигурацию виндсерфинга сетчатки и тем самым уменьшает общее смещение нижнего фронта в переднем фронте примерно на 10%. Это показывает, что конфигурация сетчатки, соответствующая мировой конфигурации, вносит вклад в окончательное восприятие - важны как сетчатые, так и мировые конфигурации.

Изменение конфигурации мира

Конфигурация виндсерфера сетчатки остается постоянной, а мировые конфигурации меняются от виндсерфинга до ВПП. Изменение мировой конфигурации от виндсерфинга до взлетно-посадочной полосы создает сильное смещение нижней стороны в переднем плане. Для всех наблюдателей, оставляя конфигурацию сетчатки в конфигурации ВПП при изменении конфигурации мира от ВПП до виндсерфера, очень мало изменяется в общей структуре ответов. Это не означает, что для некоторых наблюдателей нет никаких изменений, а скорее, что эффект ВПП, присутствующий в данных из эксперимента 2, остается в эксперименте 3А для всех наблюдателей и в той же сумме в средних данных.

Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

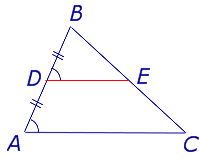
Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса , и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии - отрезки DE , EF и FD (рис.3).

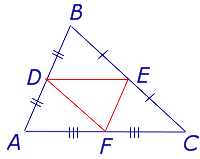
Поскольку

DE | | FC , DF | | EC ,

что и требовалось доказать.

Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

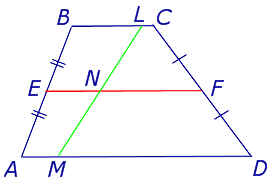
Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса , выполнено равенство: LN = NM , что и требовалось доказать.

Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

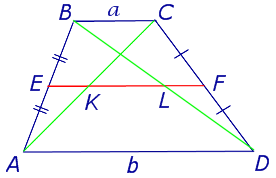
Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

Следовательно,

что и требовалось доказать.

Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

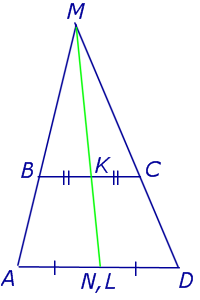
Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

Из этих соотношений получаем:

откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой .

Средние линии четырехугольника. Теорема Вариньона

Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями .

Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма .

Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

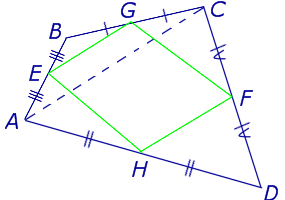
Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине . Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине . Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

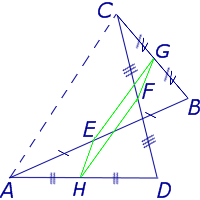
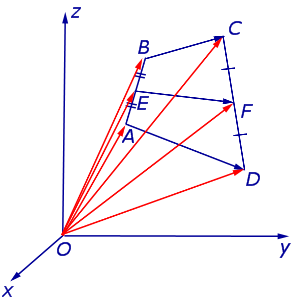
У каждого тетраэдра имеется 4 вершины , 4

Материалы по теме:

Карта сайта