Образовательный портал. Образование / Среднее образование и школа / Методы решения уравнений 4 степени. Схема Горнера. Примеры

Методы решения уравнений 4 степени. Схема Горнера. Примеры

27.06.2019

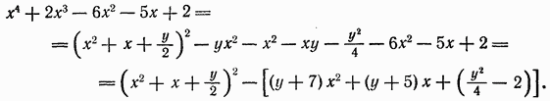
Вскоре после того, как Кардано опубликовал способ решения кубических уравнений, его ученики и последователи нашли способы сведения общего уравнения четвертой степени к кубическому уравнению. Изложим наиболее простой способ, принадлежащий Л. Феррари.

При изложении способа нужно будет воспользоваться следующей элементарной леммой.

Есть некоторые уравнения степени 4, которые чрезвычайно легко решить вручную. На ум приходит уравнение для поверхности тора. Вы можете определить корни любого решения в этом уравнении. \\ Слева ^ 2-б ^ 2. Каждый фактор будет уменьшаться на два каждый, что приведет к четырем продуктам, всего.

За меньшее количество шагов мы просто используем первый.
Теперь мы можем определить разность двух квадратов.

Это то, что вы получаете при прокалывании пончика через бок с действительно тонкой иглой.

Игла пробивает поверхность четыре раза, в четырех местах, в этих точках. Это сложное решение и может быть декодировано несколькими различными способами. Это то, что происходит, когда вы описываете тор с осью, которая существует в пустом пространстве отверстия.

Лемма. Для того чтобы квадратный трехчлен был квадратом линейного двучлена, необходимо и достаточно, чтобы его дискриминант равнялся нулю.

Доказательство. Необходимость. Пусть . Тогда Достаточность. Пусть Тогда

Идея излагаемого способа состоит в том, чтобы представить левую часть уравнения в виде разности двух квадратов. Тогда ее можно будет разложить на два множителя второй степени, и решение уравнения приведется к решению двух квадратных уравнений. Для достижения цели левую часть представим в виде:

Таким образом, когда мы выражаем как действительные, так и мнимые компоненты вместе, один, слишком упрощенный способ думать об этом, - это две реальные точки, существующие в месте расположения 2 мнимых точек, что приводит к 4-мя комплексным суммам. Там есть целая двумерная плоскость, связанная с мнимым числом. Что такое реальное приложение? При перемещении процессор решает миллионы степеней 4 уравнений тора с гораздо более сложными углами, чем только эти координатные срезы, подробно описанные выше.

Решение квадратичных уравнений. Существует 3 широко используемых метода решения квадратичных уравнений. Квадратичным уравнением является уравнение, в котором переменная имеет показатель Стандартной формы квадратичного уравнения. Квадратичные уравнения обычно имеют 2 решения.

Здесь у - вспомогательная неизвестная, которую нужно подобрать так, чтобы выражение в квадратных скобках оказалось квадратом линейного двучлена. В силу леммы для этого необходимо и достаточно выполнения условия

Это условие есть уравнение третьей степени относительно у. После раскрытия скобок оно преобразуется к виду

Пусть - один из корней этого уравнения. Тогда при условие будет выполнено, так что имеет место

Сначала уравнение должно быть записано в стандартной форме. Это означает, что многочлен должен находиться в нисходящей форме и устанавливать равным нулю. Затем вы должны указать многочлен. Когда факторизован многочлен, задайте любой фактор, который содержит переменную, равную нулю, и решит для переменной. Проверьте свой ответ в исходном уравнении. Каждое квадратичное уравнение имеет два решения, хотя в случае совершенного квадратного тринома оба решения одинаковы.

Во-первых, вы должны получить уравнение в стандартной форме. Теперь вы готовы к фактору. Установите коэффициенты равными нулю. Так как повторение дважды в качестве фактора, есть два решения, но они оба одинаковы. Таким образом, это единственное «уникальное» решение этой проблемы. Это идеальный квадрат триномии, который учитывается на квадрате бинома.

при некоторых k и I. Исходное уравнение примет вид

Приравнивая нулю каждый из сомножителей, мы найдем четыре корня исходного уравнения.

Сделаем еще одно замечание. Пусть - корни первого сомножителя, и - корни второго. Тогда Сложив эти равенства, получим, что

Таким образом, мы получили выражение корня вспомогательного кубического уравнения через корни исходного уравнения четвертой степени.

Если проблема имеет степень три, вы найдете три решения. Этот пример уравнения третьей степени имеет три решения. Прежде чем принимать квадратный корень с каждой стороны, вы должны изолировать термин, содержащий квадрат переменной. Как только этот квадратичный термин полностью изолирован, вы возьмете квадратный корень с обеих сторон и решите для переменной. Введем теперь возможность двух корней для каждого квадратного корня, одного положительного и одного отрицательного. Поместите знак перед стороной, содержащей константу, прежде чем вы возьмете квадратный корень с этой стороны.

Пример. Решить уравнение . Согласно изложенному выше методу преобразуем левую часть:

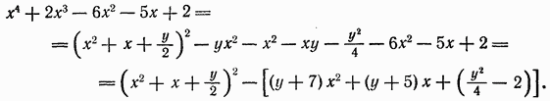
Теперь положим . После образований получим уравнение

Легко видеть, что одним из корней этого уравнения является число . Подставив его в преобразованную левую часть исходного уравнения, получим:

В каждом из первых трех примеров, включающих свойство квадратного корня, обратите внимание, что не было условий первой степени. Эти уравнения, хотя они и имеют квадратичный характер, имеют вид. Чтобы решить квадратичное уравнение, которое содержит член первой степени, используя свойство квадратного корня, было бы связано с завершением квадрата, который является еще одним «трюком», который будет объяснен в другом уроке.

Эти переменные являются коэффициентами членов квадратичного уравнения. Возможные целые решения - это делители. Дискриминант отрицательный, поэтому он не имеет реальных решений. При х = -1, если уравнение выполнено, поэтому оно является решением. Мы применяем правило Раффини для разложения уравнения.

Приравнивая сомножители нулю, получим

Что касается уравнений выше четвертой степени, то здесь были известны некоторые классы уравнений сравнительно частного вида, допускающих алгебраические решения в радикалах, т. е. в виде результатов арифметических действий и действия извлечения корня. Однако попытки дать решение общих уравнений пятой степени и выше были безуспешны, пока, наконец, в начале 19 в. Руффини и Абель не доказали, что решение такого рода для общих уравнений выше четвертой степени невозможно. Наконец, в 1830 г. гениальному французскому математику Э. Галуа удалось найти необходимые и достаточные условия (проверяемые довольно сложно) для разрешимости в радикалах конкретно заданного уравнения. При этом Галуа создал и использовал новую для своего времени теорию групп подстановок.

Тип игры:граф

Класс:8 , 9

Тема:Уравнения, приводящиеся к квадратным

Комментарий. Эта игра интересна тем, что важными и полезными являются различные пути получения результата. Это как раз пример на воплощение дидактической идеи – процесс важнее результата.

Кроме обычной организации игры с разбивкой учащихся на группы, идущие различными путями, можно предложить и фронтальный вариант, в котором учитель показывает и комментирует различные этапы решения. Разумеется, при этом ослабляется игровой характер задания, не появляется возможность в деятельностной форме ознакомить учащихся с несколькими важными алгебраическими идеями.

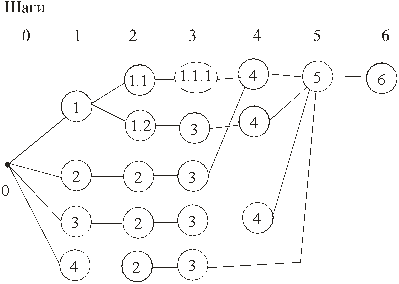
Тип игры: граф (выбор пути решения).

Дано уравнение x (x +1)(x +2)(x +3)=360.

Выберите один из возможных способов преобразования уравнения.

1. Перемножить сомножители в левой части.

2. Сгруппировать сомножители по два.

3. Использовать симметрию множителей и сделать замену .

4. Воспользоваться известным тождеством для преобразования произведения четырех подряд идущих целых чисел.

Реакция на выбор способа преобразования

1. Этот способ самый прямой, однако не ясно, приведет ли он к цели. Тем не менее, попробуйте перемножить и получить уравнение 4-ой степени вида x 4 + ax 3 + bx 2 + cx + d =0.

Закончив вычисления, перейдите к шагу 2.

Сверьте свои вычисления с правильным ответом.

x 4 +6x 3 + 11x 2 +6x –360=0

Выберите один из двух известных вам типов решения уравнения 4-ой степени.

1.1. Приведение к биквадратному уравнению с помощью удачной замены неизвестного.

1.2. Приведение к возвратному уравнению, используя симметрию коэффициентов.

Реакция на второй шаг

1.1. Это хороший путь. Чтобы подобрать замену, советуем выделить полный квадрат, используя первые два слагаемых.

Предлагайте выкладки, подберите необходимую замену и сверьте с ответом.

1.1.1. У вас должно получиться следующее уравнение:

(x 2 +3x ) 2 +2(x 2 +3x )–360=0.

Теперь замена ясна. Обозначьте новое неизвестное через y и сверьте ответ.

y 2 +2y –360=0

Решите это квадратное уравнение и запишите два его корня: y 1 = (–20), y 2 =(18).

Реакция: верно – неверно.

Для каждого найденного значения y решите уравнение x 2 +3x = y . До записи ответа укажите число корней.

Уравнение имеет (2) корня.

Запишите ответ.

x 1 =(–6), x 2 =(3)

1.2. Этот путь хороший, но нелегкий. Мешает свободный член – 360. Советуем продолжить путь обычным образом – поделить на x 2 и заменить . Не пугайтесь того, то x не исчезнет – останется слагаемое вида .

Сверьте с правильным ответом.

Слева и справа стоят полные квадраты. Воспользуйтесь этим, извлеките корни из обеих частей и перейдите к следующему шагу.

Проверьте себя, что вы не забыли извлечь корень с двумя знаками и получить два уравнения: и .

Вернитесь к неизвестному x и получите два квадратных уравнения.

x 2 +3x +20=0

x 2 +3x –18=0

До записи ответа укажите число корней исходного уравнения.

Шаги 5 и 6 совпадают с этими шагами в пути 1.1.

2. Этот путь самый естественный. Решите, какие пары множителей вы будете объединять.

Первый и второй		Неудачно, попробуйте другой способ
Третий и четвертый
Первый и третий
Второй и четвертый

Первый и четвертый		Это удачный способ, подсказанный соображениями симметрии. Сверьте ответ
Второй и третий

(x 2 +3x )(x 2 +3x +2)=360

Сделайте замену.

2.1. y = (x 2 + 3x )

2.2. y = (x 2 + 3x + 1)

2.1.Эта замена естественная, хотя и не самая лучшая. Лучше было бы заменить x 2 +3x +1 = y . Продолжите свой способ и получите квадратное уравнение относительно y .

2.2. Это очень толково. Сразу замечаете симметрию. Сверьте уравнение.

y 2 –1=360; y 2 =361

3. Это способ наиболее короткий. Сверьте запись получающегося биквадратного уравнения.