Определение логарифма и его свойства: теория и решение задач. Свойства логарифмов и примеры их решений. Исчерпывающий гид (2019)

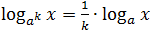
Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами .

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log a x и log a y . Тогда их можно складывать и вычитать, причем:

1. log a x + log a y = log a (x · y );
2. log a x − log a y = log a (x : y ).

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания . Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм »). Взгляните на примеры — и убедитесь:

Log 6 4 + log 6 9.

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log 6 4 + log 6 9 = log 6 (4 · 9) = log 6 36 = 2.

Задача. Найдите значение выражения: log 2 48 − log 2 3.

Основания одинаковые, используем формулу разности:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Задача. Найдите значение выражения: log 3 135 − log 3 5.

Снова основания одинаковые, поэтому имеем:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Задача. Найдите значение выражения: log 7 49 6 .

Избавимся от степени в аргументе по первой формуле:
log 7 49 6 = 6 · log 7 49 = 6 · 2 = 12

Задача. Найдите значение выражения:

[Подпись к рисунку]

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 2 4 ; 49 = 7 2 . Имеем:

[Подпись к рисунку]

Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log 2 7. Поскольку log 2 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

Пусть дан логарифм log a x . Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:

[Подпись к рисунку]

В частности, если положить c = x , получим:

[Подпись к рисунку]

Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача. Найдите значение выражения: log 5 16 · log 2 25.

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

А теперь «перевернем» второй логарифм:

[Подпись к рисунку]

Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Задача. Найдите значение выражения: log 9 100 · lg 3.

Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:

[Подпись к рисунку]

Теперь избавимся от десятичного логарифма, перейдя к новому основанию:

[Подпись к рисунку]

Основное логарифмическое тождество

Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.

Вторая формула — это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество.

В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a ? Правильно: получится это самое число a . Внимательно прочитайте этот абзац еще раз — многие на нем «зависают».

Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.

Задача. Найдите значение выражения:

[Подпись к рисунку]

Заметим, что log 25 64 = log 5 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:

[Подпись к рисунку]

Если кто-то не в курсе, это была настоящая задача из ЕГЭ:)

Логарифмическая единица и логарифмический ноль

В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

1. log a a = 1 — это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
2. log a 1 = 0 — это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a 0 = 1 — это прямое следствие из определения.

Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.

Одним из элементов алгебры примитивного уровня является логарифм. Название произошло из греческого языка от слова “число” или “степень” и означает степень, в которую необходимо возвести число, находящееся в основании, для нахождения итогового числа.

Виды логарифмов

• log a b – логарифм числа b по основанию a (a > 0, a ≠ 1, b > 0);
• lg b – десятичный логарифм (логарифм по основанию 10, a = 10);
• ln b – натуральный логарифм (логарифм по основанию e , a = e ).

Как решать логарифмы?

Логари́фм числа b по основанию a является показателем степени, которая требует, чтобы в число b возвели основание а. Полученный результат произносится так: “логарифм b по основанию а”. Решение логарифмических задач состоит в том, что вам необходимо определить данную степень по числам по указанным числам. Существуют некоторые основные правила, чтобы определить или решить логарифм, а также преобразовать саму запись. Используя их, производится решение логарифмических уравнений, находятся производные, решаются интегралы и осуществляются многие другие операции. В основном, решением самого логарифма является его упрощенная запись. Ниже приведены основные формулы и свойства:

Для любых a ; a > 0; a ≠ 1 и для любых x ; y > 0.

• a log a b = b – основное логарифмическое тождество
• log a 1 = 0
• log a a = 1
• log a (x · y ) = log a x + log a y
• log a x/ y = log a x – log a y
• log a 1/x = -log a x
• log a x p = p log a x
• log a k x = 1/k · log a x , при k ≠ 0
• log a x = log a c x c
• log a x = log b x/ log b a – формула перехода к новому основанию
• log a x = 1/log x a

Как решать логарифмы – пошаговая инструкция решения

• Для начала запишите необходимое уравнение.

Обратите внимание: если в логарифме по основанию стоит 10 , то запись укорачивается, получается десятичный логарифм. Если стоит натуральное число е, то записываем, сокращая до натурального логарифма. Имеется ввиду, что результат всех логарифмов – степень, в которую возводится число основания до получения числа b.

Непосредственно, решение и заключается в вычислении этой степени. До того как решить выражение с логарифмом, его необходимо упростить по правилу, то есть, пользуясь формулами. Основные тождества вы сможете найти, вернувшись немного назад в статье.

Складывая и вычитая логарифмы с двумя различными числами, но с одинаковыми основаниями, заменяйте одним логарифмом с произведением или делением чисел b и с соответственно. В таком случае можно применить формулу перехода к другому основания (см. выше).

Если вы используете выражения для упрощения логарифма, то необходимо учитывать некоторые ограничения. А то есть: основание логарифма а – только положительное число, но не равное единице. Число b, как и а, должно быть больше нуля.

Есть случаи, когда упростив выражение, вы не сможете вычислить логарифм в числовом виде. Бывает, что такое выражение не имеет смысла, ведь многие степени – числа иррациональные. При таком условии оставьте степень числа в виде записи логарифма.

Что такое логарифм?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")

Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно - уравнения с логарифмами.

Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 - 20 минут вы:

1. Поймете, что такое логарифм .

2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.

3. Научитесь вычислять простые логарифмы.

Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень...

Чувствую, сомневаетесь вы... Ну ладно, засекайте время! Поехали!

Для начала решите в уме вот такое уравнение:

Если Вам нравится этот сайт...

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)

можно познакомиться с функциями и производными.

Рассмотрим примеры логарифмических уравнений.

Пример 1. Решить уравнение

Для решения используем способ потенцирования. Неравенства >0 и >0 будут определять область допустимых значений уравнения. Неравенство >0 справедливо при любых значениях х, так как а 5х>0 только при положительных значения х. Значит ОДЗ уравнения — множество чисел от нуля до плюс бесконечности. Уравнение равносильно квадратному уравнению. Корни этого уравнения — числа 2 и 3,так как произведение этих чисел равно 6, а сума этих чисел равна 5 -противоположному значению коэффициента b? Оба этих числа лежат в промежутке, значит, они и есть корни этого уравнения. Заметим, что мы с лёгкостью решили данное уравнение.

Пример 2. Решить уравнение

(логарифм выражения десять икс минус девять по основанию три равен логарифму икс по основанию одна третья)

Это уравнение отличается от предыдущего тем, что логарифмы имеют разные основания. И рассмотренный метод решения уравнения здесь использовать уже нельзя, хотя можно найти область допустимых значений и попробовать решить уравнение функционально графическим методом. Неравенства >0 и x >0определяют область допустимых значений уравнения, значит. Рассмотрим графическую иллюстрацию этого уравнения. Для этого построим по точкам график функции и. Мы можем утверждать, только что у данного уравнения есть единственный корень, он положительный, лежит на интервале от 1 до 2. Точное значение корня дать не возможно.

Конечно, данное уравнение не единственное, содержащее логарифмы с разными основаниями. Решить такие уравнения можно только с помощью перехода к новому основанию логарифма. Трудности, связанные с логарифмами разных оснований могут встретиться и в других типах заданий. Например, при сравнении чисел и.

Помощником в решении таких заданий является теорема

Теорема: Если a,b,c - положительные числа, причём а и с отличны от 1, то имеет место равенство

Эта формула называется - формула перехода к новому основанию)

Таким образом, из и больше. Так как по формуле перехода к новому основанию равен и равен

Докажем теорему о переходе к новому основанию логарифма.

Для доказательства введем обозначения =m , =n , =k (логарифм числа бэ по основанию а равен эм, логарифм числа бэ по основанию цэ равен эн, логарифм числа а по основанию цэ равен ка).Тогда по определению логарифма: число b есть а в степени m, число b есть с в степени n, число a есть с в степени k. Так то подставим её значение в при возведении степени в степень показатели степеней перемножаются, получим, что =, но следовательно = , если основания степени равны, то равны и показатели данной степени=. Значит = вернемся к обратной замене: (логарифм числа бэ по основанию а равен отношению логарифма числа бэ по основанию цэ к логарифму числа а по основанию цэ)

Рассмотрим для данной теоремы два следствия.

Первое следствие. Пусть в данной теореме мы хотим перейти к основанию b. Тогда

(логарифм числа бэ по основанию бэ деленное на логарифм числа а по основанию бэ)

равен единице, то равен

Значит, если aи bположительные и отличные от 1 числа, то справедливо равенство

Следствие 2. Если a и b - положительные числа, причем а не равное единице число, то для любого числа m , не равного нулю, справедливо равенство

логарифм b по основанию а равен логарифму b в степени m по основанию a в степени m .

Докажем данное равенство справа налево. Перейдем в выражении(логарифм числа бэ в степени эм по основанию а в степени эм)к логарифму с основанием а. По свойству логарифма показатель степени подлогарифмического выражения можно вынести вперёд - перед логарифмом. =1. Получим. (дробь, в числителе эм умноженное на логарифм числа бэ по основанию а в знаменателе эм)Число m не равно нулю по условию, значит, полученную дробь можно сократить на m. Получим. Что и требовалось доказать.

Значит, для перехода к новому основанию логарифма используются три формулы

Пример 2. Решить уравнение

(логарифм выражения десять икс минус девять по основанию три равен логарифму икс по основанию одна третья )

Область допустимых значений мы нашли у данного уравнения ранее. Приведем к новому основанию 3. Для этого запишем в данный логарифм в виде дроби. В числителе будет логарифм х по основанию три, в знаменателе будет логарифм одной третьей по основанию три. равен минус одному, тогда правая часть уравнения будет равна минус

Перенесем в левую часть уравнения и запишем как. По свойству, сумма логарифмов равна логарифму произведения, значит (логарифм выражения десять икс минус девять по основанию три плюс логарифм икс по основанию три)можно записать как.(логарифм произведения десять икс минус девять и икс по основанию три) Выполним умножение, получим в левой части уравнения,

а в правой части — ноль запишем как, так как три в нулевой степени есть один.

Методом потенцирования получим квадратное уравнение =0. По свойству коэффициентов а+b+c=0 корни уравнения равны 1 и 0,1.

Но в области определения лежит только один корень. Это число один.

Пример 3. Вычислить. (три в степени четыре, умноженное на логарифм двух по основанию три плюс логарифм корня из двух по основанию пять умноженное на логарифм двадцати пяти по основанию четыре)

Для начала рассмотрим степень числа три. Если степени умножаются, то выполняется действие возведение степени в степень, таким образом, степень числа три можно записать как три в степени в четвёртой степени. Логарифмы в произведении с разным основанием, удобнее — логарифм с основанием четыре привести к основанию, связанному с пятью. Поэтому заменим на тождественно равное ему выражение. По формуле перехода к новому основанию.

По основному логарифмическому тождеству (а в степени логарифм числа бэ по основанию а равен числу бэ)

вместо получим В выражении выделим квадрат основания и подлогарифмического выражения. Получим. По формуле перехода к новому основанию, она записана справа от решения, получим вместо только. Квадратный корень из двух запишем как два в степени одна вторая и по свойству логарифма вынесем показатель степени перед логарифмом. Получим выражение. Таким образом, вычисляемое выражение примет вид…

При этом это 16, а произведение равно одному, значит значение выражения равно 16,5.

Пример 4. Вычислить, если lg2=a , lg3=b

Для вычисления воспользуемся свойствами логарифма и формулами перехода к новому основанию.

18 представим в виде произведения шести и трех. Логарифм произведения равен сумме логарифмов-множителей, то есть, где равен 1. Так как нам известны десятичные логарифмы, то перейдем от логарифма с основанием 6 к десятичному логарифму, получим дробь в числителе которой (десятичный логарифм трех) а в знаменателе (десятичный логарифм шести). При этом можно уже заменить на b. Разложим шесть на множители два и три. Полученное произведение запишем в виде суммы логарифмов lg2 и lg 3. Заменим их соответственно на aи b. Выражение примет вид: . Если данное выражение преобразовать в дробь путём приведения к общему знаменателю, то ответ получится

Для успешного выполнения заданий, связанных с переходом к новому основанию логарифма, необходимо знать формулы перехода к новому основанию логарифма

1. , где a,b,c-положительные числа, a , c
2. , где a,b-положительные числа, a , b
3. , где a,b-положительные числа a , m

Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.

Приведём примеры для понимания самого смысла логарифма:

Основное логарифмическое тождество:

Свойства логарифмов, которые необходимо всегда помнить:

*Логарифм произведения равен сумме логарифмов сомножителей.

* * *

*Логарифм частного (дроби) равен разности логарифмов сомножителей.

* * *

*Логарифм степени равен произведению показателя степени на логарифм ее основания.

* * *

*Переход к новому основанию

* * *

Ещё свойства:

* * *

Вычисление логарифмов тесно связано с использованием свойств показателей степени.

Перечислим некоторые из них:

Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный. Например:

Следствие из данного свойства:

* * *

При возведении степени в степень основание остаётся прежним, а показатели перемножаются.

* * *

Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении простых заданий можно легко допустить ошибку.

Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!

На этом всё! Успеха Вам!

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.