Щадь параллелограмма. Параллелограмм в задачах
Одну из параллельных сторон параллелограмма назовем основанием , а отрезок, опущенный из любой точки основания на противолежащую сторону – высотой параллелограмма.
Теорема . Площадь параллелограмма равна произведению его основания на высоту.
Дано: параллелограмм – ABCD, основание AD=a , высота BK=h .
Доказать: S ABCD = a h
Доказательство. Если BK и CE – перпендикуляры к прямой АD, то ∆ABK=∆DCE (так как AB=DC и проекция AK=DE). Поэтому площади этих треугольников равны. Площадь параллелограмма ABCD равна сумме двух фигур: треугольника ABK (равного ∆DCE) и трапеции KBCD. Значит, если от площади ABCD вычесть площадь треугольника ABK, получим площадь трапеции KBCD. Тогда площадь параллелограмма ABCD равна площади прямоугольника KBCЕ. А стороны этого прямоугольника равны BC=AD=а и BK=h.
Итак: S ABCD = AD BK=a h.
Фигуры с равными площадями называются равновеликими. На данном рисунке параллелограмм АВСD и прямоугольник КВСЕ – равновеликие.
Билет№12.
Числа a 1 , a 2 , a 3 , …, a n называются пропорциональными числам b 1 , b 2 , b 3 , …, b n , если выполняется равенство: a 1 /b 1 = а 2 /b 2 = a 3 /b 3 = … = a n /b n = k, где k – некоторое число, которое называют коэффициентом пропорциональности.
Пример. Числа 6; 7,5 и 15 пропорциональны числам ‑4; 5 и 10. Коэффициентом пропорциональности является число ‑1,5, поскольку
6/-4 = -7,5/5 = 15/-10 = -1,5.
Пропорциональность чисел имеет место быть, если эти числа связаны пропорцией.
Известно, что пропорцию можно составить не менее чем из четырех чисел, поэтому понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка чисел пропорциональна другой тройке, и т.д.).
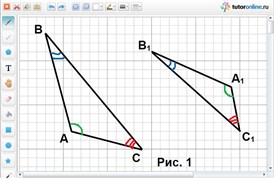
Рассмотрим на рис. 1 два треугольника АВС и А 1 В 1 С 1 с равными попарно углами: A = A 1 , B = B 1 , C = C 1 .
Стороны, которые противолежат равным парам углов обоих треугольников, называются сходственными . Так, нарис. 1 стороны AB и A 1 B 1 , AC и A 1 C 1 , BC и B 1 C 1 , сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A 1 B 1 C 1 .
Дадим определение подобных треугольников:
Два треугольника называются подобными , если их углы попарно равны, а сходственные стороны пропорциональны.
Отношение сходственных сторон подобных треугольников называется коэффициентом подобия .
Подобные треугольники обозначаются следующим образом: Δ ABC ~ Δ A 1 B 1 C 1 .
Итак, на рис. 2 имеем: Δ ABC ~ Δ A 1 B 1 C 1
углы A = A 1 , B = B 1 , C = C 1 и AB/A 1 B 1 = ВC/В 1 C 1 = АС/А 1 С 1 = k, где k – коэффициент подобия. Из рис. 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.
Замечание 1: Равные треугольники подобны с коэффициентом 1.
Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны. Например, для треугольников, изображенных на рисунке 2 говорить, что Δ ABC ~ Δ B 1 C 1 A 1 некорректно. Соблюдая правильный порядок вершин, удобно выписывать пропорцию, связывающую сходственные стороны треугольников, не обращаясь к чертежу: в числителе и знаменателе соответствующих отношений должны стоять пары вершин, занимающих одинаковые позиции в обозначении подобных треугольников. К примеру, из записи «Δ ABC ~ Δ KNL» следует, что углы A = K, B = N, C = L, и АВ/KN = BC/NL = AC/KL.
Замечание 3: Те требования, которые перечислены в определении подобных треугольников, являются избыточными. Признаки подобия треугольников, которые содержат меньше требований к подобным треугольникам докажем чуть позже.
Теорема.
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.
Доказательство.
Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA.
Проведе
Доказательство.
Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A
Теорма о средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Пусть MN - средняя линия треугольника ABC (рис 1). Докажем, что MN || AC и MN = 1/2 AC.
Т
Доказательство
Рассмотрим прямоугольник со сторонами a, b и площадью S. Докажем, что S = ab. Достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке
Теоремы о касательной к окружности.
Теорема 1. Прямая, перпендикулярная к радиусу в конечной его точке, лежащей на окружности, является касательной к окружности.
Пусть ОМ- радиус окружности, СD_|_OМ (черт
Доказательство.
Рассмотрим трапецию ABCD с основаниями AD иBC, выс
Теорема доказана.
Так же площадь трапеции можно найти с помощью следующих формул:
1. S = mh, где m - средняя линия, h - высота трапеции.
2.
Построения, основанные на свойствах прямоугольного треугольника
Задача 2.
Даны два отрезка a и b. Постройте отрезок: а) x = ; б) x =
Теорема, обратная теореме Пифагора
Теорема (теорема, обратная теореме Пифагора).
Если в треугольнике со сторонами a, b и c выполняется равенство c2 = a 2 + b 2
Площадь параллелограмма равна произведению его одной стороны на высоту, проведенную к этой стороне. Сторону, к которой проведена высота, принято называть основанием. Поэтому теорему формулируют так: площадь параллелограмма равна произведению его основания на высоту .
Если обозначить основание параллелограмма буквой a, высоту - буквой h, то площадь выражается такой формулой:
Отметим, что эта формула очень похожа на площадь прямоугольника, где она равна произведению сторон. Однако в случае параллелограмма вместо второй стороны используется высота. Причем должна быть взята та высота, которая проведена к стороне, которую берут в качестве множителя.
Доказать теорему о площади параллелограмма можно двумя способами: через площадь треугольника, через площадь прямоугольника. Рассмотрим сначала первый случай.
Пусть дан параллелограмм ABCD, в котором угол A - острый, а угол B - тупой. В таком случае, если к стороне AD из угла B провести высоту BH, то она пересечет сторону AD. Если бы высота была проведена из угла C, то она бы пересекла не сторону AD, а ее продолжение за пределами параллелограмма. Кроме того из угла B проведем диагональ.
Проведя диагональ, мы получили треугольник ABD. Его площадь равна половине от произведения его основания на высоту. В данном случае ½ * AD * BH. Доказательство площади треугольника приводится .
Поскольку диагональ BD делит параллелограмм на два равных треугольника (∆ABD = ∆CDB по трем сторонам), то его площадь равна удвоенной площади любого из этих треугольников (или сумме их площадей). Таким образом получаем, что площадь параллелограмма равна AD * BH, т. е. произведению основания на высоту.
Второй способ доказательства - через рассмотрение прямоугольника. Проведем к основанию AD две высоты. Одна из них (BH) пересечет само основание, а вторая (СI) - продолжение основания AD за пределы параллелограмма (пересечет прямую, на которой лежит AD).
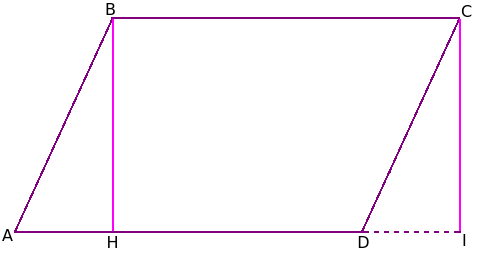
Рассмотрим треугольники ABH и DCI. Они равны друг другу (например по гипотенузе и углам BAD и CDI). Если мы рассмотрим получившийся прямоугольник HBCI, то увидим, что его площадь равна площади параллелограмма ABCD, т. к., преобразуя первый во второй, у параллелограмма «отняли» площадь ABH, а потом к нему добавили равную площадь DCI.
Площадь прямоугольника равна произведению его сторон. В данном случае BH * HI. Но HI мы можем заменить на AD, так как это равные отрезки. Таким образом получаем, что площадь прямоугольника равна BH * AD. Поскольку площади параллелограмма и прямоугольника равны, то это произведение является и площадью параллелограмма.
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
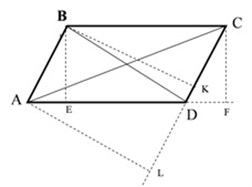
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
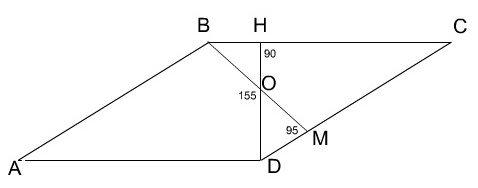
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О; <ВМD = 95 о,
 Решение.
Решение.
1. В треугольнике DОМ <МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.
2. В прямоугольном треугольнике DНС Тогда <НСD = 30 о. СD: НD = 2: 1 Но СD = АВ. Тогда АВ: НD = 2: 1. 3. <С = 30 о, 4. <А = <С = 30 о, <В = Ответ: АВ: НD = 2: 1, <А = <С = 30 о, <В = Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6. 2. К треугольнику АОD применим теорему синусов. АО/sin D = OD/sin А. 2√6/sin 45 о = OD/sin 60 о. ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6. Ответ: 12.
Задача 5.
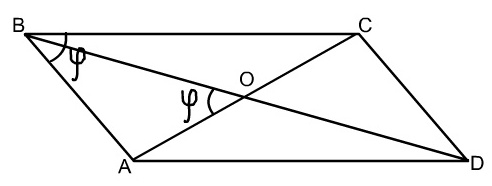
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф. 1. Посчитаем двумя разными S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф, S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф. Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или 2 · 5√2 · 7√2 = d 1 d 2 ; 2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство (АВ 2 + АD 2) · 2 = АС 2 + ВD 2 . ((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 . d 1 2 + d 2 2 = 296. 3. Составим систему: {d 1 2 + d 2 2 = 296, Умножим второе уравнение системы на 2 и сложим с первым. Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24. Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24. Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями. АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ. 4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о; d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16. d 1 2 + d 2 2 – d 1 · d 2 √2 = 64. 2. Аналогично запишем соотношение для треугольника АОD. Учтем, что <АОD = 135 о и cos 135 о = -cos 45 о = -√2/2. Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144. 3. Имеем систему Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или d 1 · d 2 = 80/(2√2) = 20√2 4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10. Примечание:
В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей. Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу. Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 . 2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1. (4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 . По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5. 3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD. ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD. ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145. Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу? www.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
(
(Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).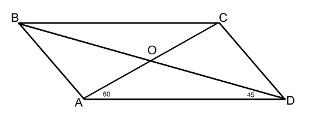
 способами его площадь.
способами его площадь.
{d 1 + d 2 = 140.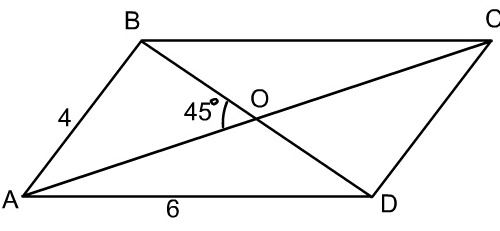
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.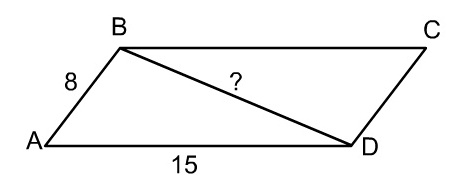
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
- Зависимость скорости ферментативной реакции от температуры, pH и времени инкубации Как влияет температура на рн
- Зависимость скорости ферментативной реакции от температуры, pH и времени инкубации Ph от температуры
- Святые богоотцы иоаким и анна Иоаким и анна когда почитание
- Храм святой великомученицы екатерины в риме
- Численность последователей основных религий и неверующих
- Абсолютные и относительные координаты Что называется абсолютными координатами точек
- Какие меры относились к политике военного коммунизма

 Live Journal
Live Journal Facebook
Facebook Twitter
Twitter