Доказать что а параллельна в. Параллельные прямые. Обратные теоремы

Вопрос: !. Докажите, что две прямые. параллельные третьей, параллельны. 2. Об"ясните, какие углы называются внутренними односторонними. Какие углы называются внутренними накрест лежащими. 3.Докажите, что если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны, а сумма внутренних односторонних углов каждой пары равны 180*

Докажите, что две прямые. параллельные третьей, параллельны. 2. Об"ясните, какие углы называются внутренними односторонними. Какие углы называются внутренними накрест лежащими. 3.Докажите, что если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны, а сумма внутренних односторонних углов каждой пары равны 180*

Ответ:

Если две прямые параллельны третьей прямой, то они параллельны. Дано: прямые a,b,c. a║c, b║c 1 Анализ: нужно доказать, прямые a и b лежат в одной плоскости и не пересекаются. Доказательство. Отметим точку D на прямой a и обозначим буквой α плоскость, проходящую через прямую b и точку D. Если допустить, что прямая a пересекает плоскость α, то по предыдущей лемме прямая c также пересечет эту плоскость, а так как c║b, то прямая b пересечет плоскость α, но этого быть не может, потому что прямая b лежит в плоскости α. Значит, прямая a принадлежит плоскости α. Таким образом, прямые a и b лежат в одной плоскости. остальные сорри не знаю(Прямые a и b не пересекаются, так как если бы они пересекались, то у них была бы общая точка (точка пересечения) и они бы имели общую параллельную им прямую, чего быть не может.

Похожие вопросы

• У Фаины на столе лежат книга и тетрадь. Помогите определить подлежащее и сказуем??е. А то учительница утверждает что "У Фаины" - подлежащее, а "лежат" - сказуемое. Спасибо!!!
• На столе лежат 4 синий и 3 красных карандаша. Редактор дважды наугад берет по одном?? карандашу и обратно их не кладет. Найти вероятность того, что: а) вторым был взят красный карандаш при условии, что первым был взят синий; б) вторым взят синий карандаш при условии, что первым оказался синий; в) вторым взят синий карандаш при условии, что первым был красный; г) вторым взят красный карандаш, при условии, что первым также оказался красный карандаш. Ребят нужно подробное решение, ибо я пропустила эту тему а разобраться не могу, помогите умоляяяю. Завтра сдавать нужно!

Страница 1 из 2

Вопрос 1. Докажите, что две прямые, параллельные третьей, параллельны.
Ответ. Теорема 4.1. Две прямые, параллельные третьей, параллельны.
Доказательство. Пусть прямые a и b параллельны прямой c. Допустим, что a и b не параллельны (рис. 69). Тогда они не пересекаются в некоторой точке C. Значит, через точку C проходят две прямые, параллельные прямой c. Но это невозможно, так как через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной. Теорема доказана.

Вопрос 2. Объясните, какие углы называются внутренними односторонними. Какие углы называются внутренними накрест лежащими?
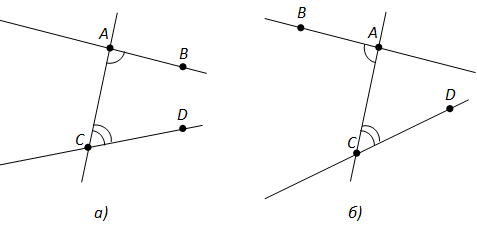
Ответ. Пары углов, которые образуются при пересечении прямых AB и CD секущей AC, имеют специальные названия.
Если точки B и D лежат в одной полуплоскости относительно прямой AC, то углы BAC и DCA называются внутренними односторонними (рис. 71, а).
Если точки B и D лежат в разных полуплоскостях относительно прямой AC, то углы BAC и DCA называются внутренними накрест лежащими (рис. 71, б).

Рис. 71

Вопрос 3. Докажите, что если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны, а сумма внутренних односторонних углов каждой пары равна 180°.
Ответ. Секущая AC образует с прямыми AB и CD две пары внутренних односторонних и две пары внутренних накрест лежащих углов. Внутренние накрест лежащие углы одной пары, например угол 1 и угол 2, являются смежными внутренним накрест лежащим углам другой пары: угол 3 и угол 4 (рис. 72).

Рис. 72

Поэтому если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны.
Пара внутренних накрест лежащих углов, например угол 1 и угол 2, и пара внутренних односторонних углов, например угол 2 и угол 3, имеют один угол общий – угол 2, а два других угла смежные: угол 1 и угол 3.
Поэтому если внутренние накрест лежащие углы равны, то сумма внутренних углов равна 180°. И обратно: если сумма внутренних накрест лежащих углов равна 180°, то внутренние накрест лежащие углы равны. Что и требовалось доказать.

Вопрос 4. Докажите признак параллельности прямых.
Ответ. Теорема 4.2 (признак параллельности прямых). Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Доказательство. Пусть прямые a и b образуют с секущей AB равные внутренние накрест лежащие углы (рис. 73, а). Допустим, прямые a и b не параллельны, а значит, пересекаются в некоторой точке C (рис. 73, б).

Рис. 73

Секущая AB разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник BAC 1 , равный треугольнику ABC, с вершиной C 1 в другой полуплоскости. По условию внутренние накрест лежащие углы при параллельных a, b и секущей AB равны. Так как соответствующие углы треугольников ABC и BAC 1 с вершинами A и B равны, то они совпадают с внутренними накрест лежащими углами. Значит, прямая AC 1 совпадает с прямой a, а прямая BC 1 совпадает с прямой b. Получается, что через точки C и C 1 проходят две различные прямые a и b. А это невозможно. Значит, прямые a и b параллельны.
Если у прямых a и b и секущей AB сумма внутренних односторонних углов равна 180°, то, как мы знаем, внутренние накрест лежащие углы равны. Значит, по доказанному выше, прямые a и b параллельны. Теорема доказана.

Вопрос 5. Объясните, какие углы называются соответственными. Докажите, что если внутренние накрест лежащие углы равны, то соответственные углы тоже равны, и наоборот.

Ответ. Если у пары внутренних накрест лежащих углов один угол заменить вертикальным ему, то получится пара углов, которые называются соответственными углами данных прямых с секущей. Что и требовалось объяснить.
Из равенства внутренних накрест лежащих углов следует равенство соответственных углов, и наоборот. Допустим, у нас есть две параллельные прямые (так как по условию внутренние накрест лежащие углы равны) и секущая, которые образуют углы 1, 2, 3. Углы 1 и 2 равны как внутренние накрест лежащие. А углы 2 и 3 равны как вертикальные. Получаем: \(\angle\)1 = \(\angle\)2 и \(\angle\)2 = \(\angle\)3. По свойству транзитивности знака равенства следует, что \(\angle\)1 = \(\angle\)3. Аналогично доказывается и обратное утверждение.
Отсюда получается признак параллельности прямых по соответственным углам. Именно: прямые параллельны, если соответственные углы равны. Что и требовалось доказать.

Вопрос 6. Докажите, что через точку, не лежащую на данной прямой, можно провести параллельную ей прямую. Сколько прямых, параллельных данной, можно провести через точку, не лежащую на этой прямой?

Ответ. Задача (8). Даны прямая AB и точка C, не лежащая на этой прямой. Докажите, что через точку C можно провести прямую, параллельную прямой AB.
Решение. Прямая AC разбивает плоскость на две полуплоскости (рис. 75). Точка B лежит в одной из них. Отложим от полупрямой CA в другую полуплоскость угол ACD, равный углу CAB. Тогда прямые AB и CD будут параллельны. В самом деле, для этих прямых и секущей AC углы BAC и DCA внутренние накрест лежащие. А так как они равны, то прямые AB и CD параллельны. Что и требовалось доказать.
Сопоставляя утверждение задачи 8 и аксиомы IX (основного свойства параллельных прямых), приходим к важному выводу: через точку, не лежащую на данной прямой, можно провести параллельную ей прямую, и только одну.

Вопрос 7. Докажите, что если две прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.

Ответ. Теорема 4.3 (обратная теореме 4.2). Если две параллельные прямые пересекаются третьей прямой, то внутренние накрест лежащие углы равны, а сумма внутренних односторонних углов равна 180°.
Доказательство. Пусть a и b – параллельные прямые и c – прямая, пересекающая их в точках A и B. Проведём через точку A прямую a 1 так, чтобы внутренние накрест лежащие углы, образованные секущей c с прямыми a 1 и b, были равны (рис. 76).
По признаку параллельности прямых прямые a 1 и b параллельны. А так как через точку A проходит только одна прямая, параллельная прямой b, то прямая a совпадает с прямой a 1 .
Значит, внутренние накрест лежащие углы, образованные секущей с
параллельными прямыми a и b, равны. Теорема доказана.

Вопрос 8. Докажите, что две прямые, перпендикулярные третьей, параллельны. Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Ответ. Из теоремы 4.2 следует, что две прямые, перпендикулярные третьей, параллельны.
Предположим, что две какие-либо прямые перпендикулярны третьей прямой. Значит, эти прямые пересекаются с третьей прямой под углом, равным 90°.
Из свойства углов, образованных при пересечении параллельных прямых секущей, следует, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.

Вопрос 9. Докажите, что сумма углов треугольника равна 180°.

Ответ. Теорема 4.4. Сумма углов треугольника равна 180°.
Доказательство. Пусть ABC – данный треугольник. Проведём через вершину B прямую, параллельную прямой AC. Отметим на ней точку D так, чтобы точки A и D лежали по по разные стороны от прямой BC (рис. 78).
Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и C равна углу ABD.
А сумма всех трёх углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD и секущей AB, то их сумма равна 180°. Теорема доказана.

Вопрос 10. Докажите, что у любого треугольника по крайней мере два угла острые.
Ответ. Действительно, допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть два угла, каждый из которых не меньше 90°. Сумма этих двух углов уже не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°. Что и требовалось доказать.