Составить уравнение всех сторон треугольника а 4. Уравнение треугольника

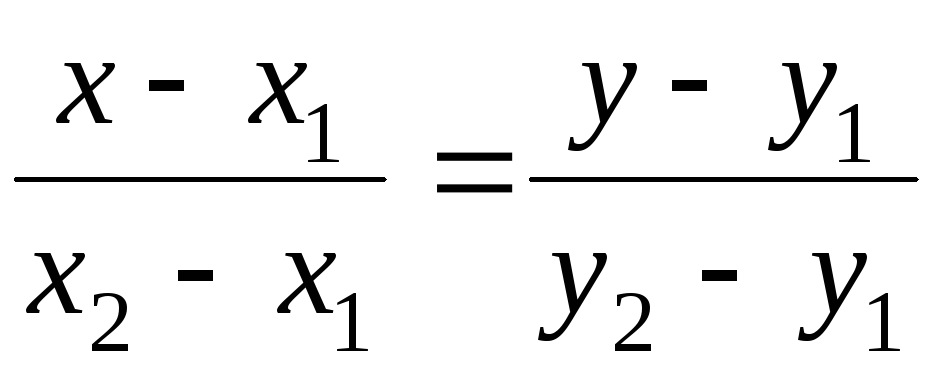
В аналитической геометрии треугольник на плоскости можно задать в декартовой системе координат. Зная координаты вершин, вы можете составить уравнения сторон треугольника. Это будут уравнения трех прямых, которые, пересекаясь, образуют фигуру.

Вам понадобится

Ручка;
- бумага для записей;
- калькулятор.

Спонсор размещения P&G Статьи по теме "Как по координатам вершин треугольника найти уравнения его сторон" Как найти длину стороны треугольника по координатам Как найти вершины углов Как составить уравнение плоскости

Инструкция

Прямая на плоскости описывается уравнением: ax+bу+с = 0, где х,y – координаты по оси 0х и оси 0у какой-либо точки прямой; a, b, с – числовые коэффициенты. Причем a и b не могут равняться нулю одновременно. Такой вид записи называется общим уравнением прямой. Также прямую можно задать выражением вида: y = kx+c. Это уравнение прямой с угловым коэффициентом k, который является тангенсом угла, образующегося при пересечении данной прямой с осью 0х. Зная координаты двух точек А (х1;y1), В (х2;у2), вы можете записать уравнение прямой, проведенной через эти точки, используя пропорцию: (у-у1)/(у1-у2)=(х-х1)/(у1-у2). Далее, преобразовав это равенство, приведите его к виду как в шаге 1 или 2.

Рассмотрите алгоритм решения задачи на конкретном примере. Даны три вершины треугольника с известными координатами: А (9;8), В (7;-6), С (-7;4). Напишите уравнение прямых, образующих его. Найдите уравнение для прямой АВ. Примените формулу из шага 3, подставив значения координат точек А и В: (у-8)/(8-(-6)) = (х-9)/(9-7). Преобразуйте его: (у-8)/14 = (х-9)/2 или 2(у-8) = 14(х-9). Сократите уравнение, разделив левую и правую части на два, и раскройте скобки: у = 7х-63+8 = 7х-55.
Уравнение для АВ: у = 7х-55. Или: 7х-у-55 = 0 (АВ). Аналогично напишите уравнение для прямой ВС: (у-(-6))/(-6-4) = (х-7)/7-(-7)). (у+6)/(-10) = (х-7)/14. 7(у+6) = -5(х-7). 7у+42 = -5х+35. 7у = -5х-7. у = -5/7х-1.
Уравнение для ВС: y = -5/7х-1. Или: -5х-7у-7 = 0 (ВС). Затем уравнение для прямой СА: (у-8)/(8-4) = (х-9)/(9-(-7)). 16(у-8) = 4(х-9). 4у-32 = х-9. 4у = х-9+32. у = 0,25х+5,75.
Уравнение для СА: у = 0,25х+5,75. Или: х-4у+23 = 0 (СА). Вы составили уравнения трех сторон фигуры. Для самопроверки постройте треугольника в системе координат. Найдите на чертеже значения пересечений прямых с осью 0у. Сравните эти координаты с полученными в уравнении. Например, для (BC) при y = 0, х = -1,4. Как просто

Другие новости по теме:

Есть множество способов определить треугольник. В аналитической геометрии один из этих способов - задать координаты трех его вершин. Эти три точки определяют треугольник однозначно, но для полноты картины нужно еще составить уравнения сторон, соединяющих вершины. Спонсор размещения P&G Статьи по

Прямая - алгебраическая линия первого порядка. В декартовой системе координат на плоскости уравнение прямой задается уравнением первой степени. Вам понадобится Знания по аналитической геометрии. Базовые знания по алгебре. Спонсор размещения P&G Статьи по теме "Как составить уравнение прямой" Как

Прямую линию можно построить по двум точкам. Координаты этих точек «спрятаны» в уравнении прямой. Уравнение расскажет о линии все секреты: как повернута, в какой стороне координатной плоскости располагается и т.д. Спонсор размещения P&G Статьи по теме "Как построить прямую" Как найти точку на

Для рассмотрения двух пересекающихся прямых достаточно рассмотрения их в плоскости, потому что две пересекающиеся прямые лежат в одной плоскости. Зная уравнения этих прямых, можно найти координату их точки пересечения. Вам понадобится уравнения прямых Спонсор размещения P&G Статьи по теме "Как

Корнем любого уравнения всегда являются некоторые точки на числовой оси. Если в уравнении одно искомое число, то располагаться оно будет на одной оси. Если два неизвестных, то эта точка будет располагаться в плоскости, на двух перпендикулярных осях. Если три - то в пространстве, на трех осях.

Чтобы найти точку пересечения прямых, достаточно рассмотреть их в плоскости, где они расположены. Далее необходимо составить уравнение этих прямых и, решив его, вы получите искомые результаты. Спонсор размещения P&G Статьи по теме "Как найти координаты точки пересечения прямых" Как вычислить точки

Линия, проведенная из вершины треугольника перпендикулярно к противоположной стороне, называется его высотой. Зная координаты вершин треугольника, можно найти его ортоцентр - точку пересечения высот. Спонсор размещения P&G Статьи по теме "Как найти координаты пересечения высот в треугольнике" Как

Любая плоскость может быть задана линейным уравнением Ax+By+Cz+D=0. Обратно, каждое такое уравнение определяет плоскость. Чтобы составить уравнение плоскости, проходящей через точку и прямую, надо знать координаты точки и уравнение прямой. Вам понадобится - координаты точки; - уравнение прямой.

Раздел V . АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

И В ПРОСТРАНСТВЕ

В раздел включены задачи, которые рассматриваются в теме «Аналитическая геометрия на плоскости и в пространстве»: составление различных уравнений прямых на плоскости и в пространстве; определение взаимного расположения прямых на плоскости, прямых, прямой и плоскости, плоскостей в пространстве; изображение кривых второго порядка. Необходимо отметить, что в данном разделе представлены задачи экономического содержания, при решении которых применяются сведения из аналитической геометрии на плоскости.

При решении задач аналитической геометрии целесообразно воспользоваться учебными пособиями следующих авторов: Д.В. Клетеника, Н. Ш. Кремера, Д.Т. Письменного В.И. Малыхина, т.к. в данной литературе рассматривается более широкий круг задач, которые можно использовать для самостоятельной подготовки по данной теме. Применение анали­тической геометрии к решению экономических задач изложено в учебных изда­ниях М.С. Красса и В.И. Ермакова.

Задача 5.1. Даны координаты вершин треугольника АВС . Необходимо

а) написать уравнения сторон треугольника;

б) написать уравнение высоты треугольника проведенной из вершины С к стороне АВ и найти ее длину;

в) написать уравнение медианы треугольника, проведенной из вершины В к стороне АС ;

г) найти углы треугольника и установить его вид (прямоугольный, остроугольный, тупоугольный);

д) найти длины сторон треугольника и определить его тип (разносторонний, равнобедренный, равносторонний);

е) найти координаты центра тяжести (точка пересечения медиан) треугольника АВС ;

ж) найти координаты ортоцентра (точка пересечения высот) треугольника АВС .

К каждому из пунктов а) – в) решения сделать рисунки в системе координат. На рисунках обозначить соответствующие пунктам задачи линии и точки.

Пример 5.1

Даны координаты вершин треугольника АВС : . Необходимо а) написать уравнения сторон треугольника; б) написать уравнение высоты треугольника проведенной из вершины С к стороне АВ и найти ее длину; в) написать уравнение медианы треугольника, проведенной из вершины В к стороне АС ; г) найти длины сторон треугольника и определить его тип (разносторонний, равнобедренный, равносторонний); д) найти углы треугольника и установить его вид (прямоугольный, остроугольный, тупоугольный); е) найти координаты центра тяжести (точка пересечения медиан) треугольника АВС ; ж) найти координаты ортоцентра (точка пересечения высот) треугольника АВС .

Решение

а) Для каждой стороны треугольника известны координаты двух точек, которые лежат на искомых линиях, значит уравнения сторон треугольника – уравнения прямых, проходящих через две заданные точки

,

где

и

соответствующие координаты точек.

Таким образом, подставляя в формулу (5.1) координаты соответствующих прямым точек получаем

,

,

,

откуда после преобразований записываем уравнения сторон

На рис. 7 изобразим соответствующие сторонам треугольника

прямые.

Ответ:

б) Пусть

– высота, проведенная из вершинык стороне

. Поскольку

проходит через точкуперпендикулярно вектору

, то составим уравнение прямой по следующей формуле

где

– координаты вектора перпендикулярного искомой прямой,

– координаты точки, принадлежащей этой прямой. Найдем координаты вектора, перпендикулярного прямой

, и подставим в формулу (5.2)

,

,

.

Найдем длину высоты CH как расстояние от точки до прямой

,

где

– уравнение прямой

,

– координаты точки.

В предыдущем пункте было найдено

Подставив данные в формулу (5.3), получим

,

На рис. 8 изобразим треугольник и найденную высоту СН .

Ответ: .

Рис. 8

в) медиана

треугольника

делит сторону

на две равные части, т.е. точкаявляется серединой отрезка

. Исходя из этого, можно найти координаты

точки

, ,

где

и

и, подставив которые в формулы (5.4), получим

;

.

Уравнение медианы

треугольника

составим как уравнение прямой, проходящей через точки

и

по формуле (5.1)

,

.

Ответ: (рис. 9).

Рис. 9

г) Длины сторон треугольника найдем как длины соответствующих векторов, т.е.

,

,

.

Стороны

и

треугольника

равны, значит, треугольник является равнобедренным с основанием

.

Ответ: треугольник

равнобедренный с основанием

;

,

.

д) Углы треугольника

найдем как углы между векторами, исходящими из соответствующих вершин данного треугольника, т.е.

,

,

.

Поскольку треугольник равнобедренный с основанием

, то

,

Углы между векторами вычислим по формуле (4.4), для которой потребуются скалярные произведения векторов

,

.

Найдем координаты и модули векторов, необходимых для вычисления углов

,

;

,

,

.

Подставляя найденные данные в формулу (4.4), получим

,

Поскольку значения косинусов всех найденных углов положительны, то треугольник

является остроугольным.

Ответ: треугольник

остроугольный;

,

,

.

е) Пусть

– центр тяжести треугольника

, тогда координаты

точки

можно найти, по формулам (5.5)

, ,

где

,

и

– координаты соответственно точек,и, следовательно,

,

.

Ответ:

– центр тяжести треугольника

.

ж) Пусть – ортоцентр треугольника

. Найдем координаты точкикак координаты точки пересечения высот треугольника. Уравнение высоты

было найдено в пунктеб) . Найдем уравнение высоты

:

,

,

.

Поскольку

, то решение системы

является координатами точки , откуда находим

.

Ответ:

– ортоцентр треугольника

.

Задача 5.2. Фиксированные издержки на предприятии при выпуске некоторой продукции составляют F V 0 руб. за единицу продукции, при этом выручка составляет R 0 руб. за единицу изготовленной продукции. Составить функцию прибыли P (q ) (q

Данные к условию задачи, соответствующие вариантам:

Пример 5.2

Фиксированные издержки на предприятии при выпуске некоторой продукции составляют

руб. в месяц, переменные издержки –

руб. за единицу продукции, при этом выручка составляет

руб. за единицу изготовленной продукции. Составить функцию прибыли P (q ) (q – количество произведенной продукции); построить ее график и определить точку безубыточности.

Решение

Вычислим совокупные издержки на производстве при выпуске q единиц некоторой продукции

Если будет продано q единиц продукции, то совокупный доход составит

Исходя из полученных функций совокупного дохода и совокупных издержек, найдем функцию прибыли

,

.

Точка безубыточности – точка, в которой прибыль равна нулю, или точка, в которой совокупные издержки равны совокупному доходу

,

,

откуда находим

–точка безубыточности.

Для построения графика (рис. 10) функции прибыли найдем еще одну точку

Ответ: функция прибыли

, точка безубыточности

.

Задача 5.3. Законы спроса и предложения на некоторый товар соответственно определяются уравнениями p = p D (q ), p = p S (q ), где p – цена на товар, q – количество товара. Предполагается, что спрос определяется только ценой товара на рынке p С , а предложение – только ценой p S , получаемой поставщиками. Необходимо

а) определить точку рыночного равновесия;

б) точку равновесия после введения налога, равного t . Определить увеличение цены и уменьшение равновесного объема продаж;

в) найти субсидию s , которая приведет к увеличению объема продаж на q 0 ед. относительно изначального (определенного в пункте а));

г) найти новую точку равновесия и доход правительства при введении налога, пропорционального цене и равного N %;

д) определить, сколько денег будет израсходовано правительством на скупку излишка при установлении минимальной цены, равной p 0 .

К каждому пункту решения сделать рисунок в системе координат. На рисунке обозначить соответствующие пункту задачи линии и точки.

Данные к условию задачи, соответствующие вариантам:

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

хорошую работу на сайт">

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Задание 1

Дан треугольник АВС, где А(1;5), В(-2;1), С(4;4). Найти:

1. Длину стороны АВ;

2. Внутренний угол А с точностью до градуса;

3. Уравнение и длину высоты, опущенной из вершины С;

4. Точку пересечения высот;

5. Уравнение медианы, проведенной через вершину С;

6. Систему линейных неравенств, определяющих треугольник АВС;

7. Сделать чертеж.

1. Длина стороны АВ.

Расстояние между двумя точками:

треугольник медиана вершина высота

2. Для нахождения внутреннего угла А определим уравнения сторон АВ и АС.

Воспользовавшись уравнением прямой, проходящей через две точки:

получим уравнение стороны АВ:

4(х-1) = -3(у-5)

4х-3у+11 = 0: АВ

и стороны АС:

-(х-1) =3(у-5)

х+3у-16 = 0: АС

Из уравнение прямой y = kx + b найдем угловой коэффициент прямой:

АВ: , тогда

АС: , тогда

Тангенс угла между двумя прямыми, угловые коэффициенты, которых соответственно равны и вычисляется по формуле

3. Уравнение и длина высоты, опущенной из вершины С.

Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид. Высота СD перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты CD, воспользуемся условием перпендикулярности прямых. Так как, то. Подставив координаты точки С и найденный угловой коэффициент высоты, получим

3х+4у-28= 0:СD

Точка пересечения прямых АВ и CD находится из системы уравнений:

Решая ее, получаем:

Длина высоты СD:

4. Точка пересечения высот.

Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид. Высота BF перпендикулярна стороне AC. Чтобы найти угловой коэффициент высоты BF, воспользуемся условием перпендикулярности прямых. Так как, то. Подставив координаты точки B и найденный угловой коэффициент высоты, получим

Точка пересечения прямых BF и DC находится из системы уравнений:

Решая ее, получаем: - точка пересечения высот.

5. Уравнение медианы СМ, проведенной через точку С. По определению медианы треугольника точка М является серединой отрезка АВ. Следовательно,

Уравнение СМ:

2(х-4) = -9(у-4)

6. Система линейных неравенств:

АВ: 4х-3у+11 = 0, С(4;4)

4*4-3*4+11 = 15>0

AC: х+3у-16 = 0, В(-2;1)

2+3*1-16 = -15<0

3(х+2) =6(у-1)

х-2у+4 = 0, А(1;5)

1-2*5+4 = -5<0

Система линейных неравенств:

Задание 2

Даны векторы Доказать, что векторы образуют базис четырехмерного пространства, и найти координаты вектора в этом базисе.

(2, -1, 0, 3) , (-1, 1, 2, 1) , (1, 0, 2, 0) , (0, 1, -1, 1) , (-1, 2, -4, 6).

Векторы образуют базис, если они линейно независимы. Это условие выполняется, если определитель матрицы системы уравнений отличен от нуля.

Следовательно, векторы образуют базис.

Для нахождения координат вектора в этом базисе решим систему уравнений методом Крамера.

б = -20/(-20) = 1

в = -20/(-20) = 1

г = 40/(-20) = -2

д = -40/(-20) = 2

Следовательно, вектор

Задание 3

Найти производные функций

Задание 4

Исследовать функцию и построить ее график.

I. Область определения:

II. Четность, периодичность:

функция является нечетной, график функции симметричен относительно начала координат. Функция непериодическая.

III. Нули функции, интервалы знакопостоянства.

Точка перегиба

VII. Построим график функции.

Задание 5

Найти неопределенные интегралы. Результат проверить дифференцированием.

Проверка:

Проверка:

Найдем по формуле интегрирования по частям:

Проверка:

Дробь представим в виде суммы простейших дробей:

Проверка:

Задание 6

Вычислить площадь фигуры, ограниченной графиками функций:

Сделаем чертеж:

Найдем точки пересечения графиков функций:

Вычислим площадь фигуры:

Размещено на Allbest.ru

...

Подобные документы

Нахождение длины сторон и площади треугольника, координат центра тяжести пирамиды, центра масс тетраэдра. Составление уравнений геометрического места точек, высоты, медианы, биссектрисы внутреннего угла, окружности. Построение системы линейных неравенств.

контрольная работа , добавлен 13.12.2012


Определение уравнения линии, уравнения и длины высоты, площади треугольника. Расчёт длины ребра, уравнения плоскости и объема пирамиды. Уравнение линии в прямоугольной декартовой системе координат. Тригонометрическая форма записи комплексных чисел.

контрольная работа , добавлен 25.03.2014


Методика нахождения уравнения прямой исследуемого треугольника и параллельной ей стороне с использованием углового коэффициента. Определение уравнения высоты этого треугольника. Порядок и составление алгоритма вычисления площади данного треугольника.

задача , добавлен 08.11.2010


Расчет площади равнобедренного и равностороннего треугольника. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. Расчет размеров медианы, биссектрисы.

презентация , добавлен 16.04.2011


Написание уравнения прямой, проходящей через определенную точку и удаленной от начала координат на заданное расстояние. Расчет длины высот параллелограмма. Построение плоскости и прямой, определение точки пересечения прямой и плоскости и угла между ними.

контрольная работа , добавлен 16.06.2012


Уравнение стороны треугольника и ее угловой коэффициент. Координаты точки пересечения медиан. Уравнение прямой, проходящей через точки. Область определения функции. Поиск производной и предела функции. Площадь фигуры, ограниченной заданными линиями.

контрольная работа , добавлен 12.05.2012


Особенности изложения школьного курса по математике по теме "Многоуголная система координат". Способы нахождения точки, которые лежат на оси абсцисс. Построение треугольника по трем точкам. Как найти координаты точек пересечения сторон треугольника.

презентация , добавлен 21.04.2011


Определение точки пересечения высот треугольника и координат вектора. Сущность базиса системы векторов и его доказательство. Определение производных функций, исследование ее и построение графика. Неопределенные интегралы и их проверка дифференцированием.

контрольная работа , добавлен 26.01.2010


Понятие треугольника и его роль в геометрии. Сумма углов треугольника, вычисление площади, свойства различных видов фигур. Признаки равенства и подобия треугольников, теорема Пифагора. Медианы, биссектрисы и высоты, соотношение между сторонами и углами.

курс лекций , добавлен 23.04.2011


Геометрическая фигура, образованная тремя фигурами, которые соединяют три не лежащие на одной прямой точки. Основные формулы площади треугольника. Решение задач на нахождение площади треугольника через две его стороны и высоту, проведенную к основанию.