Образовательный портал. Образование / Среднее образование и школа / Все определения по теме функция. Что такое функция и ее свойства. Суть понятия «функция»

Все определения по теме функция. Что такое функция и ее свойства. Суть понятия «функция»

27.07.2019

Национальный научно-исследовательский университет

Кафедра прикладной геологии

Реферат по высшей математике

На тему: «Основные элементарные функции,

их свойства и графики»

Выполнил:

Проверил:

преподаватель

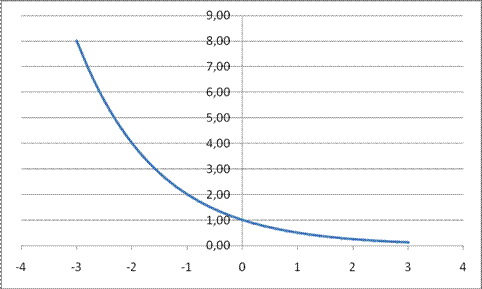
Определение. Функция, заданная формулой у=а х (где а>0, а≠1), называется показательной функцией с основанием а.

Здесь мы вводим ряд различных типов функций. Как мы увидим, каждый тип функции имеет для нее характерный граф. Область полинома есть. Еще одной важной особенностью многочлена является степень. Степень многочлена - старший коэффициент. Например, многочлен имеет.

Многочлен степени 2 называется квадратичной функцией и поэтому написан. График квадратичной функции является параболой. Если а отрицательно, парабола открыта внизу. Графы всех корневых функций проходят через точку. Эта функция имеет множество применений в физике, биологии, химии и технике.

Сформулируем основные свойства показательной функции:

1. Область определения - множество (R) всех действительных чисел.

2. Область значений - множество (R+) всех положительных действительных чисел.

3. При а > 1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает.

4. Является функцией общего вида.

, на интервале xÎ [-3;3]

Функция вида у(х)=х n , где n – число ÎR, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола).

Суть понятия «функция»

Полностью рациональная функция - отношение двух многочленов. Простейшим примером рациональной функции является ее область определения. Другим примером вполне рациональной функции является. Область определения здесь. Каждая рациональная функция автоматически является алгебраической функцией. Вот еще несколько примеров.

Тригонометрические функции являются периодическими функциями, их значения функций повторяются через регулярные интервалы. Даже если база логарифма является переменной, можно различать следующие, четко определенные логарифмы. Не используется очень часто. . Чтобы вызвать вспомогательную процедуру из другой процедуры, введите имя процедуры и вставьте значения для всех необходимых аргументов. Вызов не требуется, но если вы его используете, вы должны заключить все аргументы в круглые скобки.

Степенная функция у=х²

1. D(x)=R – функция определена на все числовой оси;

2. E(y)= и возрастает на промежутке

Степенная функция у=х³

1. График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами:

2. D(x)=R – функция определена на все числовой оси;

3. E(y)=(-∞;∞) – функция принимает все значения на своей области определения;

Вызовите подпрограммы с более чем одним аргументом

Вы можете использовать вспомогательную процедуру для организации других процедур, чтобы упростить их понимание и отладку. Сообщение отображает окно сообщения. В следующем примере показаны два способа вызова подпроцедуры с несколькими аргументами. Во втором вызове аргументы должны быть заключены в круглые скобки, потому что используется оператор вызова.

При вызове процедур функции используйте круглые скобки

Чтобы использовать возвращаемое значение функции, назначьте функцию переменной и поместите аргументы в круглые скобки. Это проиллюстрировано в следующем примере. Если вам не требуется возвращаемое значение функции, вы можете вызвать функцию, а также подпроцедуру. Оставьте круглые скобки, перечислите аргументы и не назначайте функцию любым переменным. Это показано в следующем примере.

4. При х=0 у=0 – функция проходит через начало координат O(0;0).

5. Функция возрастает на всей области определения.

6. Функция является нечетной (симметрична относительно начала координат).

, на интервале xÎ [-3;3]

В зависимости от числового множителя, стоящего перед х³, функция может быть крутой/пологой и возрастать/убывать.

Если вы вставляете круглые скобки в предыдущем примере, оператор вызывает синтаксическую ошибку. Вы можете перечислить именованные аргументы в любом порядке. Именованный аргумент состоит из имени аргумента, за которым следует двоеточие и знак равенства, и значение, назначенное аргументу. Возвращаемое значение присваивается переменной. Является правилом соответствия, так что при каждом.

Таким образом, они являются правилами ассоциации, которые устанавливают функцию. Несколько элементов домена могут иметь один и тот же элемент кодомена. Несомненно, многие люди рождались в один и тот же день. Нет примеров «У каждого студента факультета наук есть компьютер». Уверен, что есть ученики, у которых нет компьютера или даже есть студенты, которые имеют. более одного. Это правило ассоциации, которое не устанавливает функцию. То есть, каждый реальный из реальных. Как, он называется реальной функцией и как она называется реальной переменной.

Степенная функция с целым отрицательным показателем:

Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами:

1. D(x)=(-∞;0)U(0;∞) для любого n;

2. E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число;

Обратите внимание: 1 имеет двух партнеров. Наблюдение Четыре предыдущих случая могут быть функциями только с исправлением домена. Основные операции Добавление функций Вычитание функций Умножение функций Разделение функций Наблюдение Во всех случаях домен должен быть пересечением и гарантировать существование и, следовательно, возможность их добавлять. Композиция не является коммутативной. Некоторые примеры Мы проиллюстрируем некоторые примеры функций, которые являются общими в курсах дифференциального и интегрального исчисления.

Но также в делении значения должны быть удалены, когда знаменатель равен нулю. Супраъективные функции Функция имеет значение, если это означает, что каждый элемент кодомена является образом некоторого элемента области. Например, в правильном правиле следует читать изнутри. Вычисление компонентов В составной функции, как вы можете найти ее компоненты? Биективные функции Функция сказать: она биективна. Можете ли вы проиллюстрировать случай, когда? Примеры. элементов, отличных от домена. они имеют разные изображения в кодемоне. это.

3. Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число.

4. Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число.

5. Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.

То есть: наблюдение. Операция композиции очень полезна для создания большого разнообразия функций. если он является инъективным и сюръективным. Возможны четыре случая монотонности. К минимальному положительному значению, для которого выполняется это свойство. Если он периодический, это означает, что его значения повторяются регулярно. Некоторые теоремы. Это второе определение позволяет ввести, если соответственно. Скорее их графики находятся между двумя прямыми, параллельными оси х. он повторяется вправо и влево. говорится, что: он называется периодом периодического периода. ограничено, если.

, на интервале xÎ [-3;3]

Степенная функция с дробным показателем

Степенная функция с дробным показателем вида (картинка) имеет график функции, изображенный на рисунке. Степенная функция с дробным показателем степени обладает следующими свойствами: (картинка)

1. D(x) ÎR, если n – нечетное число и D(x)=

, на интервале xÎ

, на интервале xÎ [-3;3]

Логарифмическая функция у = log a x обладает следующими свойствами:

Практически это означает, что график функции в определенной области. Ограниченные функции Говорят, что она ограничена, если: эквивалентным образом сказано. Примеры Не примеры Наблюдение Ограниченные функции не могут расти или уменьшаться до бесконечности. Понятие функции, вероятно, является самой важной концепцией математики. В следующем тексте мы рассмотрим это с определенной точки зрения, сосредоточив наше внимание на графиках функций, которые являются как областью, так и набором значений, набором действительных чисел.

Это очень важно, хотя, допустим, несколько избирательная перспектива. Наша цель, однако, заключается не в замене учебников, а в том, чтобы обогатить их более подробным описанием проблемы с фиксированной точки зрения. Наш план таков. В первой части нашего обсуждения мы рассмотрим основные свойства функций; Во второй части мы рассмотрим преобразования плоскости, которые из одних функциональных графов могут производить графики других функций; В третьей части мы применяем знания из предыдущих частей к трем простейшим функциям, получая довольно богатую теорию. Схематическое изображение, которое обычно сопровождается определением функции, может выглядеть так.

1. Область определения D(x)Î (0; + ∞).

3. Функция ни четная, ни нечетная (общего вида).

4. Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1.

График функции у = log a x может быть получен из графика функции у = а х с помощью преобразования симметрии относительно прямой у = х. На рисунке 9 построен график логарифмической функции для а > 1, а на рисунке 10 - для 0 < a < 1.

Стрелки на рисунке иллюстрируют назначение. В свою очередь, аргументам 2 и 3 присваивалось одинаковое значение функции 5. Примечание. Функциональные поля иногда иногда упоминаются в определении. Обычно мы предполагаем, что функция, которую мы понимаем, достаточно хороша, когда мы можем определить.

Его нулевые места; отделения, на которых растет функция, и те, на которых она уменьшается; самые большие и наименьшие значения, которые данная функция достигает на выбранных интервалах. Благодаря этим знаниям и некоторой дополнительной информации, во многих случаях мы уже можем набросать график функции, который в лучшем случае лучше всего иллюстрирует эту функцию. Поэтому, прежде чем мы рассмотрим сами графики, мы внимательно рассмотрим перечисленные выше функции. Мы должны сначала определить их.

; на интервале xÎ

Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями.

Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная.

Функция y = sin (х).

3. Функция периодическая; основной период равен 2π.

Пример. По аналогии мы определяем убывающие и убывающие функции. Специальное имя также является функцией, которая принимает только одно значение. Строго растущие и уменьшающиеся функции являются примерами функций с добавленной стоимостью. Деля 39 на 7, легко видеть, что \\.

Подсказка. Знаменатель должен отличаться от нуля. Так как произведение двух чисел равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, знаменатель не выдерживает ни нуля, ни минус пять. Следовательно, область функций есть множество \\.

Нам нужно иметь: \\, а также: \\. Таким образом, областью функции является множество: \\. Задача Найти набор значений функций. Поэтому каждое целое число является значением функции. Кроме того, значение функции должно быть целым числом. Он растет, но он неуклонно растет.

4. Функция нечетная.

5. Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.

График функции у = sin (х) изображен на рисунке 11.

; на интервале xÎ [-2;2]

Функция y = cos(х).

1. Область определения D(x) ÎR.

2. Область значений E(y) Î [ - 1; 1].

3. Функция периодическая с основным периодом 2π.

4. Функция четная.

5. Функция убывает на промежутках и возрастает на промежутках [-π+ 2πn; 2πn], nπZ.

График функции у = соs (х) изображен на рисунке 12.

; на интервале xÎ [-2;2]

Функция y = tg х.

1. Область определения: D(x) Ï π/2 + πk, kÎZ.

2. Область значений E(y) Î (- ∞; + ∞)

3. π- основной период функции.

4. Функция нечетная.

5. Функция возрастает на промежутках (-π/2 +πn;π/2 +πn).

График функции у = tg х изображен на рисунке 13.

; на интервале xÎ (- ;)

Функция y = ctg х.

1. Область определения функции: D(x) Ï xπ/2 +πk, kÎZ.

2. Область значений функции E(y) Î (- ∞; + ∞).

3. Функция периодическая с основным периодом π.

4. Функция нечетная.

5. Функция у = ctg х убывает на промежутках (πn;π+πn).

График функции у = ctg х изображен на рисунке 14.

; на интервале xÎ (-𝜋;)

Функции y = arcsin (х), у = arccos (х), у = arctg (х), у = arcctg (х) называют обратными тригонометрическими функциями.

Функция y = arcsin ( x ):

Свойства функции y = arcsin (x):

3. y=arcsin(x)- непрерывная строговозрастающая функция на D

5. График y = arcsin(x) симметричен графику y = sin(x) относительно линии y=x

6. y=arcsin(x) нечетная функция т.е. ∀x∈[−1;1] arcsin(−x)=−arcsin(х)

График функции y = arcsin (x) изображен на рисунке 15.

; на интервале xÎ [- ;]

Функция y = arccos ( x ):

Свойства функции y = arccos (x):

1. Область определения D(x)Î[−1;1]

2. Область значения E(y)Î

3. y=arccos(x)- непрерывная строговозрастающая функция на D

5. График y = arccos(x) симметричен графику y = cos(x) относительно линии y=x

6. y=arccos(x) функция общего вида

График функции y = arccos (x) изображен на рисунке 16.

; на интервале xÎ [- ;]

Функция y = arctg ( x ):

Свойства функции y = arctg (x):

2. Область значения E(y)Î [−π/2;π/2]

3. y=arctg (x)- непрерывная строговозрастающая функция на D

4. График y = arctg(x) симметричен графику y = tg(x) относительно линии y=x

5. y=arctg(x) нечетная функция.

График функции y = arctg (x) изображен на рисунке 17.

; на интервале xÎ [- 5; 5]

Функция y = arc с tg ( x ):

Свойства функции y = arcсtg (x):

1. Область определения D(x)Î(- ∞;+∞)

2. Область значения E(y)Î

3. y=arctg (x)- непрерывная строгоубывающая функция на D

4. График y = arcсtg(x) симметричен графику y = сtg(x) относительно линии y=x

5. y=arcctg(x) функция общего вида.

График функции y = arcctg (x) изображен на рисунке 18.

1. Алгебра и начала анализа, учебник для 10 класса общеобразовательных учреждений; С.М. Никольский; М. Просвещение, 2001

2. Конспект лекции по высшей математике.

Некоторые изображения взяты из сети Интернет, графики функции построены в программе MicrosoftOfficeExel.

Раздел II. Введение в математический анализ.

Цель. Расширить понятие функции, известное студентам из школьного курса математики. Рассмотреть понятие области определения как множество точек числовой оси. Рассмотреть способы задания функции; понятие сложной функции. Рассмотреть линейную функцию.

Задача лекции – научиться находить область определения функции; строить прямую линию по заданному в различных формах условию; разбираться во взаимном расположении прямых на плоскости.

4.1. Числовые множества. Абсолютная величина числа, ее свойства.

4.2. Функция одной переменной. Способы задания.

4.3. Элементарные функции. Краткий обзор основных элементарных функций. Преобразования графиков.

4.4. Уравнение линии на плоскости. Линейная функция. Различные уравнения прямой линии.

4.1. Числовые множества. Абсолютная

величина числа и ее свойства.

В основе математики, как и любой науки, лежат первичные понятия, не определяемые через более простые понятия. К ним относятся: число, точка, множество.

Под множеством понимается совокупность (набор) объектов, обладающих некоторым общим свойством. Эти объекты называются элементами или точками множества (множество студентов в данной аудитории, множество звезд на небе, множество букв в алфавите и так далее).

Множества обозначаются прописными буквами: A, B, X, Y , …, а их элементы соответствующими строчными буквами. Если элемент х принадлежит множеству Х , что записывают , или Х=(х 1 , х 2 ,…, х n).

Если элемент у не принадлежит множеству Y , то записывается . Если в множестве не содержится ни одного элемента, то оно называется пустым множеством и обозначается – Ø. Например, множество действительных корней уравнения является пустым.

Если элементами множества являются числа, то оно называется числовым или точечным , так как всякое действительное число можно изобразить точкой на числовой оси (числовой прямой) . Поэтому понятия «число х » и «точка х » можно считать эквивалентными.

Среди числовых множеств различают:

1. интервал (открытый отрезок) (а ;b ): это есть множество чисел, удовлетворяющих неравенству , (рис. 4.1)

2. сегмент (закрытый отрезок) [a ;b ]: это множество чисел, удовлетворяющих неравенству , (рис. 4.2)

3. полуинтервалы и (рис. 4.3) среди этих множеств могут быть бесконечные, когда и полубесконечные: (-∞ ;a ), (b ;+∞ ), (-∞ ;a ] и [b ;+∞ ). Все указанные множества объединяются одним термином – промежутки Х .

Следует различать такие понятия: объединение множеств, пересечение и разность множеств.

Абсолютная величина числа и ее свойства.

Определение. Абсолютной величиной (или модулем ) действительного числа х называется само число х , если оно неотрицательное, и противоположное число (-х ), если оно отрицательное: