Разложение многочленов на множители онлайн калькулятор. Как разложить на множители алгебраическое уравнение. Разложение на множители квадратных уравнений

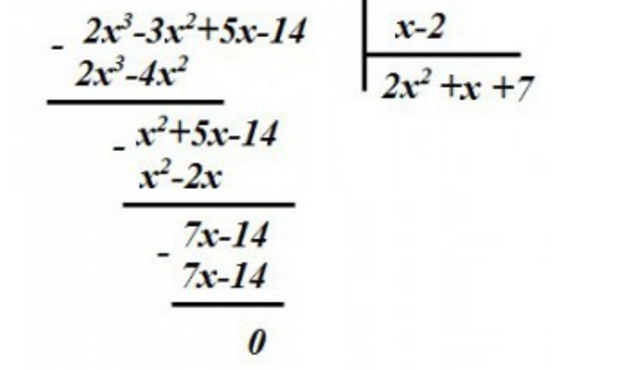
Разложение на множители уравнения – это процесс нахождения таких членов или выражений, которые, будучи перемноженными, приводят к начальному уравнению. Разложение на множители является полезным навыком для решения основных алгебраических задач, и становится практически необходимым при работе с квадратными уравнениями и другими многочленами. Разложение на множители используется для упрощения алгебраических уравнений, чтобы облегчить их решение. Разложение на множители может помочь вам исключить определенные возможные ответы быстрее, чем вы это сделаете, решая уравнение вручную.

Шаги

Разложение на множители чисел и основных алгебраических выражений

1. Разложение на множители чисел. Концепция разложения на множители проста, но на практике разложение на множители может оказаться непростой задачей (если дано сложное уравнение). Поэтому для начала рассмотрим концепцию разложения на множители на примере чисел, продолжим с простыми уравнениями, а затем перейдем к сложным уравнениям. Множители данного числа – это числа, которые при перемножении дают исходное число. Например, множителями числа 12 являются числа: 1, 12, 2, 6, 3, 4, так как 1*12=12, 2*6=12, 3*4=12.

   Отдел, квадратный корень, радикалы, фракции

   Калькулятор следует стандартным порядкам операций, которые преподаются большинством книг по алгебре - скобки, экспоненты, умножения и разделения, сложения и вычитания. Разделение, квадратный корень, радикалы и фракции не поддерживаются. Чтобы получить доступ к другим ресурсам алгебры, например. Перестаньте бороться и начинайте учиться сегодня с тысяч бесплатных ресурсов! Мы рассмотрим исключения в этой статье. В этом процессе также показаны соответствующие примеры.

   До этого, однако, вы должны знать, как выполнять умножение и лучше всего знать биномиальные формулы. Факторинг заключается в исключении общих чисел или переменных. Имеет смысл, что вы сначала освоите умножение скобок. Потому что теперь мы позаботимся об этом по-другому. Первый небольшой вводный пример.

   • Аналогично, вы можете рассматривать множители числа как его делители, то есть числа, на которые делится данное число.
   • Найдите все множители числа 60. Мы часто используем число 60 (например, 60 минут в часе, 60 секунд в минуте и т.д.) и у этого числа довольно большое количество множителей.
     • Множители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60.

2. Запомните: члены выражения, содержащие коэффициент (число) и переменную, также могут быть разложены на множители. Для этого найдите множители коэффициента при переменной. Зная, как разложить на множители члены уравнений, можно легко упростить данное уравнение.

   В обоих терминах присутствует число 4. Это мы тянем перед кронштейном. Для лучшего понимания еще нескольких примеров. Что касается некоторых более простых примеров исключения или с ними, то необходимо было найти общую переменную или число или распознать множество с числами. Вы можете узнать, правильно ли вы сделали исключение, в котором вы снова умножаете результат и, надеюсь, снова получите начальное выражение. Затем мы рассмотрим несколько более сложных задач.

   Полином с вещественными коэффициентами, который может быть выражен как произведение. два или более многочлена с вещественными коэффициентами, называемые факторами. Чтобы полностью определить многочлен, нужно выразить его как. умножение 2 или более неприводимых многочленов.

   • Например, член 12x может быть записан в виде произведения 12 и х. Вы также можете записать 12x как 3(4x), 2(6x) и т.д., разложив число 12 на наиболее подходящие вам множители.
     • Вы можете раскладывать 12x несколько раз подряд. Другими словами, вы не должны останавливаться на 3(4x) или 2(6x); продолжите разложение: 3(2(2x)) или 2(3(2x)) (очевидно, что 3(4x)=3(2(2x)) и т.д.)

3. Примените распределительное свойство умножения для разложения на множители алгебраических уравнений. Зная, как разложить на множители числа и члены выражения (коэффициенты с переменными), вы можете упростить несложные алгебраические уравнения, найдя общий множитель числа и члена выражения. Обычно для упрощения уравнения необходимо найти наибольший общий делитель (НОД). Такое упрощение возможно благодаря распределительному свойству умножения: для любых чисел а, b, с верно равенство a(b+c) = ab+ac.

   Факторизация трехчленов второй степени с переменной. Первый факторинговый метод: Общая формула. Вычисляется дискриминант. Используется общая формула. Практика: Составьте следующие триномии. Второй метод: факторинг путем проверки или подсчета очков. Чтобы определить некоторые триномы с этим методом, вы можете следовать следующему. шаги.

   Факторы расположены горизонтально. Практика: Оцените следующие триномы методом осмотра. Третий метод: использование калькулятора. Дискриминант рассчитывается, чтобы определить, является ли он факторизуемым. Наконец, полученные решения равны нулю. триномиальные факторы. Практика. Заполните следующую таблицу в соответствии с запросом.

   • Пример. Разложите на множители уравнение 12х + 6. Во-первых, найдите НОД 12x и 6. 6 является наибольшим числом, которое делит и 12x, и 6, поэтому вы можете разложить данное уравнение на: 6(2x+1).
   • Этот процесс также верен для уравнений, в которых есть отрицательные и дробные члены. Например, х/2+4 может быть разложено на 1/2(х+8); например, -7x+(-21) может быть разложено на -7(х+3).

Разложение на множители квадратных уравнений

1. Убедитесь, что уравнение дано в квадратичной форме (ax 2 + bx + c = 0). Квадратные уравнения имеют вид: ax 2 + bx + c = 0, где а, b, с - числовые коэффициенты отличные от 0. Если вам дано уравнение с одной переменной (х) и в этом уравнении есть один или несколько членов с переменной второго порядка, вы можете перенести все члены уравнения на одну сторону уравнения и приравнять его к нулю.

   Разложение на множители квадратных уравнений

   Четвертый метод: Факторинг по замечательным формулам. Этот метод используется, если выражение является идеальным квадратным трехчленом и может быть. используйте первую и вторую заметную формулу, то есть. Например: мы факторизуем, вы получаете следующее. решений и поэтому не может быть учтен.

   Чтобы определить идеальный квадратный триномиал, вы можете следовать следующему. шаги. Тринома упорядочен по убыванию по отношению к переменной. Вычислим квадратные корни конечных членов. Убедитесь, что центральный член упорядоченного тринома равен удвоенному. произведения корней, полученных на шаге. Факторы записываются с использованием результатов корней и разделяются. по знаку среднего срока.

   • Например, дано уравнение: 5x 2 + 7x - 9 = 4x 2 + x – 18. Оно может быть преобразовано в уравнение x 2 + 6x + 9 = 0, которое является квадратным уравнением.
   • Уравнения с переменной х больших порядков, например, x 3 , x 4 и т.д. не являются квадратными уравнениями. Это кубические уравнения, уравнения четвертого порядка и так далее (только если такие уравнения не могут быть упрощены до квадратных уравнений с переменной х в степени 2).

2. Квадратные уравнения, где а = 1, раскладываются на (x+d)(x+e), где d*е=с и d+е=b. Если данное вам квадратное уравнение имеет вид: x 2 + bx + c = 0 (то есть коэффициент при x 2 равен 1), то такое уравнение можно (но не гарантированно) разложить на вышеуказанные множители. Для этого нужно найти два числа, которые при перемножении дают «с», а при сложении – «b». Как только вы найдете такие два числа (d и е), подставьте их в следующее выражение: (x+d)(x+e), которое при раскрытии скобок приводит к исходному уравнению.

   Факторинг по общему коэффициенту. Общим фактором многочлена является многочлен, являющийся фактором каждого члена. этого многочлена. Чтобы определить это, выполните следующие шаги. Вычисляется максимальный общий делитель числовых коэффициентов. Переменные, которые повторяются во всех членах, выбираются с наименьшим. показатель.

   Когда у вас есть общий коэффициент, вы делите каждый член многочлена на коэффициент. общий. Написано умножение общего коэффициента и добавление отношений. получен. Пример. Обозначим следующие полиномы. Разделите каждый термин на общий коэффициент. Факторинг путем группировки и общего фактора.

   • Например, дано квадратное уравнение x 2 + 5x + 6 = 0. 3*2=6 и 3+2=5, поэтому вы можете разложить данное уравнение на (х+3)(х+2).
   • В случае отрицательных членов внесите следующие незначительные изменения в процесс разложения на множители:
     • Если квадратное уравнение имеет вид x 2 -bx+c, то оно раскладывается на: (х-_)(х-_).
     • Если квадратное уравнение имеет вид x 2 -bx-c, то оно раскладывается на: (х+_)(х-_).
   • Примечание: пробелы могут быть заменены на дроби или десятичные числа. Например, уравнение x 2 + (21/2)x + 5 = 0 раскладывается на (х+10)(х+1/2).

3. Разложение на множители методом проб и ошибок. Несложные квадратные уравнения можно разложить на множители, просто подставляя числа в возможные решения до тех пор, пока вы не найдете правильного решения. Если уравнение имеет вид ax 2 +bx+c, где a>1, возможные решения записываются в виде (dx +/- _)(ex +/- _), где d и е - числовые коэффициенты отличные от нуля, которые при перемножении дают а. Либо d, либо e (или оба коэффициента) могут быть равны 1. Если оба коэффициента равны 1, то воспользуйтесь способом, описанным выше.

   Этот метод можно использовать, когда в полиноме все члены не имеют. У них общий фактор, но вы можете группировать термины, которые имеют некоторые. общий коэффициент. Слагаемые, которые имеют некоторый общий коэффициент, сгруппированы. Он учитывает общий факторный метод, каждая из созданных групп. в шаге Это снова учитывается общим этапом фактора.

   Разложение на множители чисел и основных алгебраических выражений

   Примечание: если вы не можете определить коэффициент по второму коэффициенту во второй раз, вы должны начать все заново. выполнять новые группировки. Примеры. Обозначим следующие полиномы. группа. Факторинг по разности квадратов. Чтобы применить метод, вы должны выполнить следующие шаги. Квадратный корень каждого члена вычисляется.

   • Например, дано уравнение 3x 2 - 8x + 4. Здесь 3 имеет только два множителя (3 и 1), поэтому возможные решения записываются в виде (3x +/- _)(х +/- _). В этом случае, подставив вместо пробелов -2, вы найдете правильный ответ: -2*3x=-6x и -2*х=-2x; - 6x+(-2x)=-8x и -2*-2=4, то есть такое разложение при раскрытии скобок приведет к членам исходного уравнения.

При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим, каким образом это сделать проще всего.

Как обычно, обратимся за помощью к теории.

Теорема Безу утверждает, что остаток от деления многочлена на двучлен равен .

Но для нас важна не сама теорема, а следствие из нее:

Если число является корнем многочлена , то многочлен делится без остатка на двучлен .

Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на , где - корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.

Эта задача распадается на две: как найти корень многочлена, и как разделить многочлен на двучлен .

Остановимся подробнее на этих моментах.

1. Как найти корень многочлена.

Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.

Здесь нам помогут такие факты:

Если сумма всех коэффициентов многочлена равна нулю, то число является корнем многочлена.

Например, в многочлене сумма коэффициентов равна нулю: . Легко проверить, что является корнем многочлена.

Если сумма коэффициентов многочлена при четных степенях равна сумме коэффициентов при нечетных степенях, то число является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку , а - четное число.

Например, в многочлене сумма коэффициентов при четных степенях : , и сумма коэффициентов при нечетных степенях : . Легко проверить, что является корнем многочлена.

Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.

Для приведенного многочлена степени (то есть многочлена, в котором старший коэффициент - коэффициент при - равен единице) справедлива формула Виета:

Где - корни многочлена .

Есть ещё формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.

Из этой формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.

Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.

Рассмотрим, например, многочлен

Делители свободного члена: ; ; ;

Сумма всех коэффициентов многочлена равна , следовательно, число 1 не является корнем многочлена.

Сумма коэффициентов при четных степенях :

Сумма коэффициентов при нечетных степенях :

Следовательно, число -1 также не является корнем многочлена.

Проверим, является ли число 2 корнем многочлена: , следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен делится без остатка на двучлен .

2. Как разделить многочлен на двучлен.

Многочлен можно разделить на двучлен столбиком.

Разделим многочлен на двучлен столбиком:

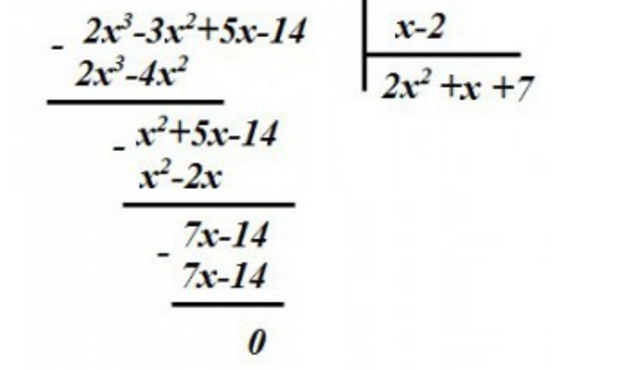
Есть и другой способ деления многочлена на двучлен - схема Горнера.

Посмотрите это видео, чтобы понять, как делить многочлен на двучлен столбиком, и с помощью схемы Горнера.

Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на её месте пишем 0 - так же, как при составлении таблицы для схемы Горнера.

Итак, если нам нужно разделить многочлен на двучлен и в результате деления мы получаем многочлен , то коэффициенты многочлена мы можем найти по схеме Горнера:

Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число является корнем многочлена , то остаток от деления многочлена на равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.

Используя схему Горнера, мы "убиваем двух зайцев": одновременно проверяем, является ли число корнем многочлена и делим этот многочлен на двучлен .

Пример. Решить уравнение:

1. Выпишем делители свободного члена, и будем искать корни многочлена среди делителей свободного члена.

Делители числа 24:

2. Проверим, является ли число 1 корнем многочлена.

Сумма коэффициентов многочлена , следовательно, число 1 является корнем многочлена.

3. Разделим исходный многочлен на двучлен с помощью схемы Горнера.

А) Выпишем в первую строку таблицы коэффициенты исходного многочлена.

Так как член, содержащий отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при пишем 0. Слева пишем найденный корень: число 1.

Б) Заполняем первую строку таблицы.

В последнем столбце, как и ожидалось, мы получили ноль, мы разделили исходный многочлен на двучлен без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:

Легко проверить, что числа 1 и -1 не являются корнями многочлена

В) Продолжим таблицу. Проверим, является ли число 2 корнем многочлена :

Так степень многочлена, который получается в результате деления на единицу меньше степени исходного многочлена, следовательно и количество коэффициентов и количество столбцов на единицу меньше.

В последнем столбце мы получили -40 - число, не равное нулю, следовательно, многочлен делится на двучлен с остатком, и число 2 не является корнем многочлена.

В) Проверим, является ли число -2 корнем многочлена . Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:

Отлично! В остатке мы получили ноль, следовательно, многочлен разделился на двучлен без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена на двучлен в таблице изображены зеленым цветом.

В результате деления мы получили квадратный трехчлен , корни которого легко находятся по теореме Виета:

Итак, корни исходного уравнения :

{}

Ответ: {}