5 разложение числа на простые множители. Учебник. Разложение выражений на множители. Тесты на определение уровня овладения

Тема урока: «Разложение чисел на простые множители».

Цель урока: выработать навык разложения чисел на простые множители, повторить признаки делимости чисел и использовать их при разложении чисел на простые множители, продолжать расширять представления учащихся об окружающем их мире.

ХОД УРОКА

Учитель: Добрый день, ребята. Садитесь. Откройте тетради и запишите число, классная работа. Тема нашего урока «Разложение чисел на простые множители».
Давайте вспомним, что это значит? Какие числа являются простыми? Какие еще вы знаете числа? К какой группе относится число 1? Теперь мы повторим, изученные нами, признаки делимости чисел на 3, 9, 5, 2 и 10. (Фронтально)

1) Работа в парах. Задание учащимся: заполнить таблицу:

«ш» 312 «ч» 310
«е» 567 «в» 585
«ы» 555 «б» 771

Ответ :

Историческая справка: Пафнутий Львович Чебышев – русский математик. Он занимался изучением свойств простых чисел. Он доказал, что между любым натуральным числом, большим 1, и числом, вдвое большим, всегда имеется не менее одного простого числа. Давайте проверим это на примере нескольких чисел. (Устно)

2) Задание учащимся: Соедините стрелками равные выражения, предварительно разложив числа из левого столбика на простые множители.

На доске записано:

125 2 . 2 . 2 . 2 . 7

315 5 . 5 . 5

444 2 . 2 . 3 . 13

112 2 . 2 . 3 . 37

156 3 . 3 . 5 . 7

Детьми вычислительной деятельностью

Группируйте учащихся по парам и передавайте наборы карт стоимости места, по одному для каждой пары. Объясните, что пары будут играть в игру. Первый ученик использует карты стоимости места для составления номера в расширенной форме и показывает его второму ученику. Второй студент пишет стандартную форму номера на листе бумаги и показывает его первому ученику, чтобы он мог подтвердить или отклонить.

В следующий период собирайте карты стоимости места и перераспределяйте числовые карточки, выставляя карты как можно более равномерно, чтобы каждый учащийся имел только 1 или 2 карты в своих руках. Например, если у вас есть 28 учеников, каждый студент получит 1 карту. Если у вас меньше учеников, некоторые студенты могут получить 2 карты. Если у вас более 28 учеников, попросите учащихся, чтобы все могли участвовать.

Как по-другому можно записать выражения, стоящие в правом столбике?

24 . 7, 53, 22 . 3 . 13, 22 . 3 . 37, 32 . 5 . 7.

2) Проверьте правильность разложения чисел на простые множители, поставив знаки «+» или «–».

3) Задание учащимся: из чисел 84, 44, 75, 60 выберите то, которое раскладывается на наибольшее количество простых множителей. Подчеркните это число зеленым цветом.

4) Работа по группам

Задание учащимся: по разложениям чисел определите, какие из них делятся на 2, на 3, на 4, на 6, на 7:

1. 2 . 11 . 13
2. 2 . 5 . 3 . 17
3. 3 . 5 . 23 . 41
4. 2 . 2 . 2 . 3 . 7.

Выпишите отдельно разложения чисел, делящихся: на число 4; на число 6.

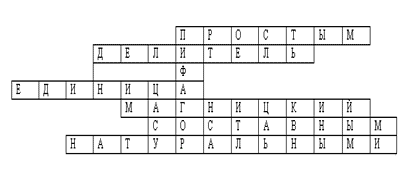
5) Отвечая на вопросы, впишите верные слова и в выделенном столбце получите имя ученого, математика, жившего до нашей эры.

1. Продолжите предложение: натуральное число, имеющее только два делителя называется …
2. Как называется натуральное число, на которое число а делится без остатка?
3. Какое число является делителем любого натурального числа?
4. Назовите автора первого учебника по математике.
5. Продолжите предложение: натуральное число, имеющее более двух делителей, называется …
6. Как называются числа, используемые при счете?

Ответы:

В данном кроссворде «спрятано» имя Пифагора Самосского (VI в. до н.э.). Историческая справка на эту тему: Пифагор и его ученики изучали вопросы делимости чисел. Число, равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, 6 = 1 + 2 + 3; 28 = 1 + 2 + 4 + 7 + 14; 496; 8 128.

Подведение итогов урока: Давайте подведем небольшой итог. Какова была цель урока? Мы её достигли?

Домашнее задание: п.41, № 495(3), №503, №507 (2).

Изучение приёмов преобразования уравнений начнём с обсуждения того, как можно разлагать на множители выражения, входящие в данное уравнение. Вообще представление уравнения f (x) = g (x) в виде F 1 (x) ċ F 2 (x) ċ ... ċ F n (x) = 0,

где выражения F k (x), k = 1, ..., n «проще» функций f (x) и g (x) , представляет собой несомненное продвижение в решении уравнения. В самом деле, представление вида (5) позволяет сразу приравнивать множители F k (x) нулю и решать более простые уравнения. Представление уравнения (1) в виде (5) иногда называют факторизованным видом уравнения (1) (от английского слова «factor» – множитель) .

Перечислим теперь некоторые наиболее распространённые приёмы разложения многочленов, как наиболее простых алгебраических функций, на множители.

1. Вынесение общего множителя за скобку

В том случае, когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена.

x 5 – 2x 3 + x 2 .

Каждое слагаемое этого многочлена содержит множитель x 2 . Вынесем его за скобку и получим ответ: x 5 – 2x 3 + x 2 = x 2 (x 3 – 2x + 1) .

2. Применение формул сокращённого умножения

Формулы сокращения довольно эффективно применяются при разложении многочлена на множители. Полезно помнить следующие формулы: a 2 - b 2 = (a - b) (a + b) , a 3 + b 3 = (a + b) (a 2 - a b + b 2) , a 3 - b 3 = (a - b) (a 2 + a b + b 2) , a 4 - b 4 = (a 2 - b 2) (a 2 + b 2) = (a - b) (a + b) (a 2 + b 2) , a 5 - b 5 = (a - b) (a 4 + a 3 b + a 2 b 2 + a b 3 + b 4) , a n - b n = (a - b) (a n - 1 + a n - 2 b + a n - 3 b 2 + a n - 4 b 3 + ... + a 2 b n - 3 + a b n - 2 + b n - 1) , n ∈ ℤ .

Разложить на множители многочлен (x – 2) 4 – (3x + 1) 4 .

Разложим разность четвёртых степеней по формуле, приведённой выше: (x - 2) 4 - (3 x + 1) 4 = ((x - 2) 2 - (3 x + 1) 2) ((x - 2) 2 + (3 x + 1) 2) = = (x - 2 - 3 x - 1) (x - 2 + 3 x + 1) (x 2 - 4 x + 4 + 9 x 2 + 6 x + 1) = = - (2 x + 3) (4 x - 1) (10 x 2 + 2 x + 5) .

3. Применение выделения полного квадрата

Без преувеличения можно сказать, что метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов. Поясним сказанное на примере.

Разложить на множители многочлен x 4 + 4x 2 – 1 .

Имеем x 4 + 4 x 2 - 1 = x 4 + 2 ċ 2 ċ x 2 + 4 - 4 - 1 = (x 2 + 2) 2 - 5 = (x 2 + 2 - 5) (x 2 + 2 + 5) .

4. Группировка

Метод группировки слагаемых, как правило, применяется совместно с другими методами разложения на множители и чаще всего с методом вынесения за скобки. Суть метода состоит в том, что все слагаемые данного многочлена перегруппировываются таким образом, чтобы в каждой группе, возможно после вынесения общего множителя за скобки, образовалось бы одно и то же выражение. Это выражение можно также вынести за скобки как общий для всех групп множитель.

5. Метод неопределённых коэффициентов

Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной.

Теоретической основой метода являются следующие утверждения.

• Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
• Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
• Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.

Для доказательства второго утверждения вспомним, как выглядит график степенной функции с нечетной целой степенью (§ 2.2.5). Действительно, из его вида следует, что значение многочлена имеет разные знаки при x → +∞ и x → –∞ . Многочлен степени n – непрерывная функция, значит, найдется хотя бы одна точка, в которой график этой функции пересечет ось Ox .

Разложить на множители многочлен 3x 3 – x 2 – 3x + 1 .

Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax 2 + bx + c такие, что справедливо равенство 3x 3 – x 2 – 3x + 1 = (x – p)(ax 2 + bx + c) = ax 3 + (b – ap)x 2 + (c – bp)x – pc.

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырёх уравнений для определения четырёх неизвестных коэффициентов: { a = 3 b - a p = - 1 c - b p = - 3 - p c = 1 Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1.

Итак, многочлен 3x 3 – x 2 – 3x + 1 разлагается на множители: 3x 3 – x 2 – 3x + 1 = (x – 1)(3x 2 + 2x – 1).

6. Теорема о корнях многочлена

Разложение многочлена на множители иногда удаётся провести, если один из его корней угадан с помощью теоремы о рациональных корнях, доказанной в § 2.1.4 . После того, как корень x = α угадан, многочлен P n (x) представим в виде P n (x) = (x – α) ċ P n – 1 (x) , где P n – 1 (x) − многочлен степени на 1 меньше, чем P n (x) .

Разложить на множители многочлен x 3 – 5x 2 – 2x + 16 .

Данный многочлен имеет целые коэффициенты. По следствию теоремы о рациональных корнях (см. § 2.1.4) если целое число является корнем этого многочлена, то оно является делителем числа 16, то есть если у данного многочлена есть целые корни, то это могут быть только числа ±1, ±2, ±4, ±8, ±16.

Проверкой убеждаемся, что число 2 является корнем этого многочлена, то есть x 3 – 5x 2 – 2x + 16 = (x – 2) ċ Q (x) , где Q (x) − многочлен второй степени. Следовательно, исходный многочлен разлагается на множители, один из которых (x – 2 ).

7. Разложение относительно параметра

Суть этого метода легче всего понять на примере.

Разложить на множители многочлен x 4 – 10x 2 – x + 20 .

Преобразуем данный многочлен: x 4 – 10x 2 – x + 20 = x 4 – 5 ċ 2x 2 – x + 25 – 5 = 25 – 5(1 + 2x 2) + x 4 – x

Рассмотрим теперь многочлен a 2 – a(1 + 2x 2) + x 4 – x , который при a = 5 совпадает с данным. Полученный многочлен является квадратным, его корни легко найти по теореме Виета: a 2 – a(1 + 2x 2) + x 4 – x = a 2 – a(1 + 2x 2) + x(x 3 – 1) = a 2 – a(1 + 2x 2) + x(x – 1)(x 2 + x + 1). Следовательно, a 1 = x(x – 1), a 2 = x 2 + x + 1 . Значит, исходный многочлен разлагается на множители a 2 – a(1 + 2x 2) + x 4 – x = (a – (x 2 – x))(a – (x 2 + x + 1)) . Вернемся к многочлену, данному в условии задачи, подставив a = 5 . Получим: x 4 – 10x 2 + x + 20 = (5 – x 2 + x)(5 – x 2 – x – 1) = (x 2 – x – 5)(x 2 + x – 4).