Разложение третьей степени. Способы разложения на множители многочлена степени выше второй. Разложение на множители многочлена с рациональными корнями

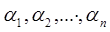
Любой алгебраический многочлен степени n может быть представлен в виде произведения n-линейных множителей вида и постоянного числа, которое является коэффициентов многочлена при старшей ступени х, т.е.

где - являются корнями многочлена.

Корнем многочлена называют число (действительное или комплексное), обращающее многочлен в нуль. Корнями многочлена могут быть как действительные корни, так и комплексно-сопряженные корни, тогда многочлен может быть представлен в следующем виде:

Рассмотрим методы разложения многочленов степени «n» в произведение множителей первой и второй степени.

Способ №1. Метод неопределенных коэффициентов.

Коэффициенты такого преобразованного выражения определяются методом неопределенных коэффициентов. Суть метода сводится к тому, что заранее известен вид множителей, на которые разлагается данный многочлен. При использовании метода неопределённых коэффициентов справедливы следующие утверждения:

П.1. Два многочлена тождественно равны в случае, если равны их коэффициенты при одинаковых степенях х.

П.2. Любой многочлен третьей степени разлагается в произведение линейного и квадратного множителей.

П.3. Любой многочлен четвертой степени разлагается на произведение двух многочленов второй степени.

Пример 1.1. Необходимо разложить на множители кубическое выражение:

П.1. В соответствии с принятыми утверждениями для кубического выражения справедливо тождественное равенство:

П.2. Правая часть выражения может быть представлена в виде слагаемых следующим образом:

П.3. Составляем систему уравнений из условия равенства коэффициентов при соответствующих степенях кубического выражения.

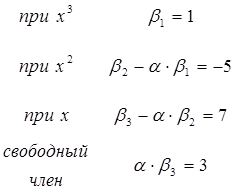
Данная система уравнений может быть решена методом подбора коэффициентов (если простая академическая задача) или использованы методы решения нелинейных систем уравнений. Решая данную систему уравнений, получим, что неопределённые коэффициенты определяются следующим образом:

Таким образом, исходное выражение раскладывается на множители в следующем виде:

Данный метод может использоваться как при аналитических выкладках, так и при компьютерном программировании для автоматизации процесса поиска корня уравнения.

Способ №2. Формулы Виета

Формулы Виета - это формулы, связывающие коэффициенты алгебраических уравнений степени n и его корни. Данные формулы были неявно представлены в работах французского математика Франсуа Виета (1540 - 1603). В связи с тем, что Виет рассматривал только положительные вещественные корни, поэтому у него не было возможности записать эти формулы в общем явном виде.

Для любого алгебраического многочлена степени n, который имеет n-действительных корней,

справедливы следующие соотношения, которые связывают корни многочлена с его коэффициентами:

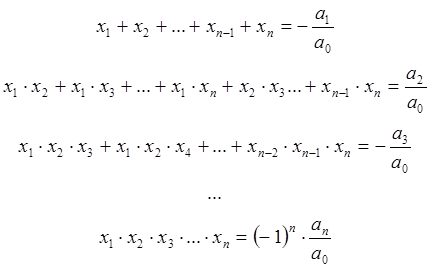
Формулами Виета удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.

Пример 2.1. Рассмотрим, как связаны корни многочлена с его коэффициентами на примере кубического уравнения

В соответствии с формулами Виета взаимосвязь корней многочлена с его коэффициентами имеет следующий вид:

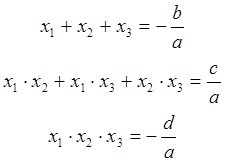
Аналогичные соотношения можно составить для любого полинома степени n.

Способ №3. Разложение квадратного уравнения на множители с рациональными корнями

Из последней формулы Виета следует, что корни многочлена являются делителями его свободного члена и старшего коэффициента. В связи с этим, если в условии задачи задан многочлен степени n c целыми коэффициентами

то данный многочлен имеет рациональный корень (несократимая дробь), где p - делитель свободного члена , а q – делитель старшего коэффициента . В таком случае многочлен степени n можно представить в виде (теорема Безу):

Многочлен , степень которого на 1 меньше степени начального многочлена, определяется делением многочлена степени n двучлен , например, с помощью схемы Горнера или самым простым способом - «столбиком».

Пример 3.1. Необходимо разложить многочлен на множители

П.1. В связи с тем, что коэффициент при старшем слагаемом равен единицы, то рациональные корни данного многочлена являются делителями свободного члена выражения, т.е. могут быть целыми числами . Подставляем каждое из представленных чисел в исходное выражение найдем, что корень представленного многочлена равен .

Выполним деление исходного многочлена на двучлен:

Воспользуемся схемой Горнера

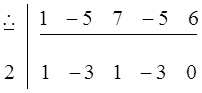
В верхней строке выставляются коэффициенты исходного многочлена, при этом первая ячейка верхней строки остается пустой.

В первой ячейке второй строки записывается найденный корень (в рассматриваемом примере записывается число «2»), а следующие значения в ячейках вычисляются определенным образом и они являются коэффициентами многочлена, который получится в результате деления многочлена на двучлен. Неизвестные коэффициенты определяются следующим образом:

Во вторую ячейку второй строки переносится значение из соответствующей ячейки первой строки (в рассматриваемом примере записывается число «1»).

В третью ячейку второй строки записывается значение произведения первой ячейки на вторую ячейку второй строки плюс значение из третьей ячейки первой строки (в рассматриваемом примере 2 ∙1 -5 = -3).

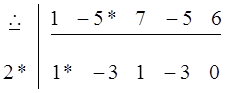
В четвертую ячейку второй строки записывается значение произведения первой ячейки на третью ячейку второй строки плюс значение из четвертой ячейки первой строки (в рассматриваемом примере 2 ∙ (-3) +7 = 1).

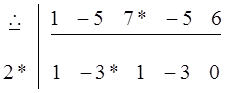
Таким образом, исходный многочлен раскладывается на множители:

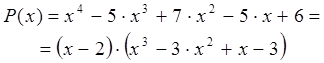
Способ №4. Использование формул сокращенного умножения

Формулы сокращенного умножения применяют для упрощения вычислений, а также разложение многочленов на множители. Формулы сокращенного умножения позволяют упростить решение отдельных задач.

Формулы, используемые для разложения на множители

Разложение многочлена на множители. Часть 1

Разложение на множители - это универсальный прием, помогающий решить сложные уравнения и неравенства. Первая мысль, которая должна прийти в голову при решении уравнений и неравенств, в которых в правой части стоит ноль - попробовать разложить левую часть на множители.

Перечислим основные способы разложения многочлена на множители :

• вынесение общего множителя за скобку
• использование формул сокращенного умножения
• по формуле разложения на множители квадратного трехчлена
• способ группировки
• деление многочлена на двучлен
• метод неопределенных коэффициентов

В этой статье мы остановимся подробно на первых трех способах, остальные рассмотрим в следующих статьях.

1. Вынесение общего множителя за скобку.

Чтобы вынести за скобку общий множитель надо сначала его найти. Коэффициент общего множителя равен наибольшему общему делителю всех коэффициентов.

Буквенная часть общего множителя равна произведению выражений, входящих в состав каждого слагаемого с наименьшим показателем степени.

Схема вынесения общего множителя выглядит так:

Внимание!
Количество членов в скобках равно количеству слагаемых в исходном выражении. Если одно из слагаемых совпадает с общим множителем, то при его делении на общий множитель, получаем единицу.

Пример 1.

Разложить на множители многочлен:

Вынесем за скобки общий множитель. Для этого сначала его найдем.

1.Находим наибольший общий делитель всех коэффициентов многочлена, т.е. чисел 20, 35 и 15. Он равен 5.

2. Устанавливаем, что переменная содержится во всех слагаемых, причем наименьший из её показателей степени равен 2. Переменная содержится во всех слагаемых, и наименьший из её показателей степени равен 3.

Переменная содержится только во втором слагаемом, поэтому она не входит в состав общего множителя.

Итак, общий множитель равен

3. Выносим за скобки множитель пользуясь схемой, приведенной выше:

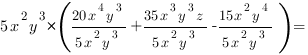
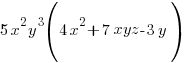
Пример 2. Решить уравнение:

Решение. Разложим левую часть уравнения на множители. Вынесем за скобки множитель :

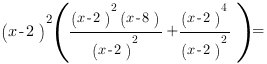
Итак, получили уравнение

Приравняем каждый множитель к нулю:

Получаем - корень первого уравнения.

Корни :

Ответ: -1, 2, 4

2. Разложение на множители с помощью формул сокращенного умножения.

Если количество слагаемых в многочлене, который мы собираемся разложить на множители меньше или равно трех, то мы пытаемся применить формулы сокращенного умножения.

1. Если многочлен представляет собой разность двух слагаемых , то пытаемся применить формулу разности квадратов :

или формулу разности кубов :

Здесь буквы и обозначают число или алгебраическое выражение.

2. Если многочлен представляет собой сумму двух слагаемых, то, возможно, его можно разложить на множители с помощью формулы суммы кубов :

3. Если многочлен состоит из трех слагаемых, то пытаемся применить формулу квадрата суммы :

или формулу квадрата разности :

Или пытаемся разложить на множители по формуле разложения на множители квадратного трехчлена :

Здесь и - корни квадратного уравнения

Пример 3. Разложить на множители выражение:

Решение. Перед нами сумма двух слагаемых. Попытаемся применить формулу суммы кубов. Для этого нужно сначала каждое слагаемое представить в виде куба какого-то выражения, а затем применить формулу для суммы кубов:

Пример 4. Разложить на множители выражение:

Рещение. Перед нами разность квадратов двух выражений. Первое выражение: , второе выражение:

Применим формулу для разности квадратов:

Раскроем скобки и приведем подобные члены, получим: