Образовательный портал. Образование / Среднее образование и школа / В трапеции проведены диагонали. Запоминаем и применяем свойства трапеции. Свойства средней линии трапеции

В трапеции проведены диагонали. Запоминаем и применяем свойства трапеции. Свойства средней линии трапеции

01.11.2018

В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию , решение которых требует знания ее свойств.

Выясним, какими же интересными и полезными для решения задач свойствами обладает трапеция.

После изучения свойства средней линии трапеции можно сформулировать и доказать свойство отрезка, соединяющего середины диагоналей трапеции . Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

В своем решении Луис Герман использует известный результат, но мало кто осознает его важность. Этот результат, хотя и элементарный, позволяет очень эффективно решать некоторые проблемы. С этим результатом немецкий мог вычислить площадь рассматриваемого треугольника, не вычисляя все ее стороны. Из этих равенств легко закончить, мы только разделяем и уже.

Не так уж сложно повторно использовать технику, используемую Луисом Германом для решения целого ряда проблем типа: найти область фигуры, зная, что другие похожи. Но мы также можем решать проблемы в другом направлении, где даются области и предпринимаются меры.

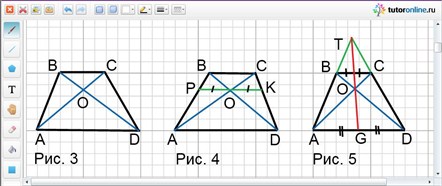
MO – средняя линия треугольника ABC и равна 1/2ВС (рис. 1).

MQ – средняя линия треугольника ABD и равна 1/2АD.

Тогда OQ = MQ – MO, следовательно, OQ = 1/2AD – 1/2BC = 1/2(AD – BC).

При решении многих задач на трапецию одним из основных приемов является проведение в ней двух высот.

Рассмотрим следующую задачу .

Пусть BT – высота равнобедренной трапеции ABCD с основаниями BC и AD, причем BC = a, AD = b. Найти длины отрезков AT и TD.

Затем мы можем использовать изученные отношения. Если бы мы не знали взаимосвязи между областями и причиной сходства, это стоило бы нам больше работы для решения проблемы. Изучите другие возможности, и вы увидите, что любой другой требует больше работы.

Свойства трапеции, вписанной в окружность

Как мы видели, эта связь полезна. И это требует практики, чтобы узнать, когда ее использовать, но важно учитывать это при решении таких проблем. Возможно, многие из вас слышали, что для Олимпиады требуется только гений, а отчасти это правда, но это также требует изучения.

Решение.

Решение задачи не вызывает затруднения (рис. 2) , но оно позволяет получить свойство высоты равнобедренной трапеции, проведенной из вершины тупого угла : высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований.

Чтобы быть хорошим олимпийцем, вам нужно узнать этот тип результатов и многие другие. Ну, как вы видели, не зная результата, как это означает, нужно усложнять экзамен, потому что им нужно будет заполнить этот недостаток гениальным. Когда они поднимаются на позиции Олимпиады, они значительно увеличивают количество теорем, которые они должны знать. И, если вы их не знаете, вы не достигнете гения, чтобы заполнить так много недостатков.

Короче говоря, это требует гения и изучения. Итак, обратите пристальное внимание на все, чему вас учат, все ценно, даже если вы не заметите его вначале. Проект направлен на то, чтобы помочь вам в дополнительных занятиях по субботам по математике, физике и химии, как это было сделано в прошлом году. Важно помнить, что проект никоим образом не предполагает замены школьных классов, а скорее дополняет их. За последний год математические модули немного выросли, и теперь они работают над раздаточными материалами. Справочники тщательно разработаны для лучшего изучения контента, открытого в классе. Распродажи разделены на главы с пояснительным текстом содержания, смешанными с решенными упражнениями и примерами, а в конце каждой главы предлагаются предлагаемые упражнения для проверки обучения, чрезвычайно важно, чтобы эти упражнения изучались. Упражнения, которые сложнее, и вы не понимаете, скажите одному из наших учителей, что возможное будет сделано для разрешения сомнения. Изучим прямые линии, углы, многоугольники и т.д. это содержание, которое служит основой для всей геометрии. Знак точки карандаша на бумаге дает представление о том, что такое точка. Линия: две разные точки определяют одну проходящую через них линию. Коллинеарные точки: это точки, принадлежащие к одной и той же строке. Плоскость. Три неколлинеарные точки определяют проходящую через них одну плоскость. Копланарные точки: это точки, принадлежащие к одной и той же плоскости. Учитывая два разных момента, встреча этих двух точек с множеством точек, находящихся между ними, является отрезком линии. Последовательные сегменты: два прямых сегмента являются последовательными, если конец одного из них также является концом другого. Коллинеарные сегменты: два линейных сегмента коллинеарны, если они находятся на одной линии. Смежные сегменты: два соседних и коллинеарных сегмента смежны, только один конец является общим, т.е. не имеет общих внутренних точек. Конгруэнтные сегменты: это те, которые имеют одинаковую меру. Примечание: ~ - это символ соответствия. Единица измерения угла соответствует отношению одной степени. Два соседних угла смежны тогда и только тогда, когда они не имеют общих внутренних точек. Обратите внимание, что две конкурирующие линии определяют две пары противоположных углов вершины. Найдите область круговой коронки. . Трапеция представляет собой выпуклый четырехугольник и считается заметной при наличии некоторых интересных свойств.

При изучении свойств трапеции нужно обратить внимание на такое свойство, как подобие. Так, например, диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики. Это утверждение можно назвать свойством треугольников, на которые разбивается трапеция ее диагоналями . Причем первая часть утверждения доказывается очень легко через признак подобия треугольников по двум углам. Докажем вторую часть утверждения.

Одним из них является свойство трапециевидной базы, которая представляет собой полусумму оснований трапеции. Параллельные противоположные стороны называются основаниями, а противоположные поперечные стороны называются только сторонами. Вычислите ширину других шагов.

Свойства трапеции, описанной около окружности

Лестницу можно рассматривать как трапецию. Если он содержит нечетное число шагов, достаточно знать, сколько первых и последних мер для вычисления среднего шага при условии, что расстояния между этапами являются постоянными. Четырехугольник, только одна пара противоположных сторон которого параллельна, называется трапецией.

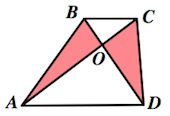
Треугольники BOC и COD имеют общую высоту (рис. 3) , если принять за их основания отрезки BO и OD. Тогда S BOC /S COD = BO/OD = k. Следовательно, S COD = 1/k · S BOC .

Аналогично, треугольники BOC и АОВ имеют общую высоту, если принять за их основания отрезки CO и OA. Тогда S BOC /S AOB = CO/OA = k и S А O В = 1/k · S BOC .

Из этих двух предложений следует, что S COD = S А O В.

Параллельные стороны трапеции называются основаниями и непрерывными бедрами. Если бедра равны, трапеция называется равнобедренной. Расстояние между основами называется высотой трапеции. Секция, соединяющая бедра с трапецией, называется серединой трапеции. Средняя линия трапеции параллельна ее основам.

Права, которые проходят через середину одной из бедер трапеции и параллельно основаниям, делят другое бедро. Средняя трапеция равна полушарию ее основ. Основная задача: доказать, что средняя часть трапеции разбивает каждую линию, края которой лежат на двух основаниях.

Не будем останавливаться на сформулированном утверждении, а найдем связь между площадями треугольников, на которые разбивается трапеция ее диагоналями . Для этого решим следующую задачу.

Пусть точка O – точка пересечения диагоналей трапеции АBCD с основаниями BC и AD. Известно, что площади треугольников BOC и AOD равны соответственно S 1 и S 2 . Найти площадь трапеции.

Сегмент, соединяющий круги на двух сторонах треугольника, называется средним сегментом треугольника. Он параллелен третьей стране и равен половине ее. Теорема: право, проходящее через середину одной стороны треугольника и параллельное другой стороне треугольника, видит свою третью сторону.

Примените свойства средних сегментов в треугольнике и трапеции

Тогда мы действуем так же, как в случае. Повторите, во-первых, как вы измеряете треугольник и угловую линию? Можете ли вы написать окружность любого полигона? Если ваши предыдущие вопросы не вызвали никаких проблем, вам не о чем рассказать, как вы получаете окружность трапеции.

Так как S COD = S А O В, то S АВС D = S 1 + S 2 + 2S COD .

Из подобия треугольников BОC и AOD следует, что ВО/OD = √(S₁/S 2).

Следовательно, S₁/S COD = BO/OD = √(S₁/S 2), а значит S COD = √(S 1 · S 2).

Тогда S АВС D = S 1 + S 2 + 2√(S 1 · S 2) = (√S 1 + √S 2) 2 .

С использованием подобия доказывается и свойство отрезка, проходящего через точку пересечения диагоналей трапеции параллельно основаниям .

Например, все данные должны быть переданы на одни и те же единицы. на дециметрах

Пример 1: Рассчитать трапецеидальные схемы, показанные на рисунке. Трапецеидальная окружная цепь 1. Итак, что это за трапеция? Что нам делать, чтобы получить окружность трапеции? Пример 2. Рассчитайте количество отсутствующих частей трапеций, показанных на изображении.

Трапецеидальная сторона изображения 1. Трапециевидная сторона рисунка 2: вы можете снова увидеть на картинке, что это грубая трапеция. Вы выигрываете результат, и вы получаете два оружия. Не забудьте объединить устройства. Личи имеет те же длинноглазые брови - так что он довольно плоский.

Рассмотрим задачу :

Пусть точка O – точка пересечения диагоналей трапеции ABCD с основаниями BC и AD. BC = a, AD = b. Найти длину отрезка PK, проходящего через точку пересечения диагоналей трапеции параллельно основаниям. На какие отрезки делится PK точкой О (рис. 4)?

Из подобия треугольников AOD и BOC следует, что АO/OС = AD/BC = b/a.

Действуйте в соответствии со следующими инструкциями. Теперь попытка ответить на мои вопросы. Отвечая на ваш вопрос, сравните со мной, что сразу под данным вопросом. Они являются верхними углами, и поэтому они одинаковы. Все, что вы только что обнаружили, было замечено на следующей картинке.

Признак и свойство вписанной и описанной трапеции

Это, конечно, не удивляет вас тем, что они одинаковы. Сфера применения: Нарисуйте произвольную трапецию и помощник с трапецией и одной из бровей, чтобы показать, что содержание трапеции действительно действительно. Ответьте на следующие вопросы. Вы можете найти ответ на следующем рисунке.

Из подобия треугольников AOР и ACB следует, что АO/AС = PO/BC = b/(a + b).

Отсюда PO = BC · b / (a + b) = ab/(a + b).

Аналогично, из подобия треугольников DOK и DBC, следует, что OK = ab/(a + b).

Отсюда PO = OK и PK = 2ab/(a + b).

Итак, доказанное свойство можно сформулировать так: отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции.

Какие плоские самолеты делают ученый разделить трапецию? Итак, вы скажете содержимое трапеции. Содержание трапеции определяется тем, что вы производите длину двух оснований высотой, и результат будет равен двум. Пример 4. Определите содержание трапеций в изображении.

Содержание трапеции на рисунке 1. Содержание трапеции на рисунке 2: Не забудьте объединить единицы. Содержание трапеции синего цвета действительно для. Мы будем считать поток, как и в предыдущих случаях. Прежде всего, мы читаем рабочие листы корзин и высоты трапеции.

Теперь мы можем легко прочитать содержимое трапеции. Мы делим всю картину на несколько самолетов, содержание которых вы можете испортить. Одно из возможных разделов можно увидеть на следующем рисунке. Содержание зеленой части. Содержание синей части. Содержание желтой части.

Следующее свойство четырех точек : в трапеции точка пересечения диагоналей, точка пересечения продолжения боковых сторон, середины оснований трапеции лежат на одной линии.

Треугольники BSC и ASD подобны (рис. 5) и в каждом из них медианы ST и SG делят угол при вершине S на одинаковые части. Следовательно, точки S, T и G лежат на одной прямой.

Общее содержание плоской фигуры. Пример 9. Сначала пытается решить проблему. После списка рабочих листов следуют результаты и предложения для отдельных переводов. Рисунок 5: Какова площадь собаки на картинке на картинке. Укажите его высоту, если она имеет основы 15 дм и 5 дм.

Трапецеидальные хвойные породы - задачи

Получение рисунка на поперечной продольной трапеции. Существует трапеция, в которой угол между основанием и плечами составляет 45 градусов. Если угол между основанием и плечом равен 45 градусам, высота трапеции составляет разницу между основаниями, разделенными на 2.

Точно так же на одной прямой расположены точки T, O и G. Это следует из подобия треугольников BOC и AOD.

Значит, все четыре точки S, T, O и G лежат на одной прямой.

Так же можно найти длину отрезка разбивающего трапецию на две подобных.

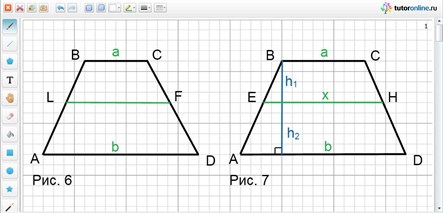
Если трапеции ALFD и LBCF подобны (рис. 6), то a/LF = LF/b.

Отсюда LF = √(ab).

Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований .

Трапециевидная вогнутая конструкция

Мы строим структуру следующим образом. Правильно соединяя нижнюю часть основания с точками пересечения, мы получаем трапецию. Вот решение вашей задачи. Два угла в основании основания острые, а два на более коротком основании открыты. В целом, углы трапеции имеют одинаковые 360 градусов. Вы имеете в виду строительство такой трапеции? Угол 45 градусов, например, между диагональной стороной квадрата и углом 30 градусов между высотой и стороной треугольного треугольника.

Передняя стенка дымовой камеры камина, показанная на рисунке, имеет форму трапеции. Рука трапеции составляет 70 см в длину и наклоняется к основанию трапеции под углом 45 °. Вычислите окружность этой трапеции, зная, что плечи образуют основание угла 30 градусов.

Докажем свойство отрезка, делящего трапецию на две равновеликие .

Пусть площадь трапеции равна S (рис. 7). h 1 и h 2 – части высоты, а х – длина искомого отрезка.

Тогда S/2 = h 1 · (a + x)/2 = h 2 · (b + x)/2 и

S = (h 1 + h 2) · (a + b)/2.

Составим систему

{h 1 · (a + x) = h 2 · (b + x)
{h 1 · (a + x) = (h 1 + h 2) · (a + b)/2.

Решая данную систему, получим х = √(1/2(а 2 + b 2)).

Таким образом, длина отрезка, делящего трапецию на две равновеликие, равна√((а 2 + b 2)/2) (среднему квадратичному длин оснований).

Итак, для трапеции ABCD с основаниями AD и BC (BC = a, AD = b) доказали, что отрезок:

1) MN, соединяющий середины боковых сторон трапеции, параллелен основаниям и равен их полусумме (среднему арифметическому чисел a и b);

2) PK, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, равен
2ab/(a + b) (среднему гармоническому чисел a и b);

3) LF, разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому чисел a и b, √(ab);

4) EH, делящий трапецию на две равновеликие, имеет длину √((а 2 + b 2)/2) (среднее квадратичное чисел a и b).

Признак и свойство вписанной и описанной трапеции.

Свойство вписанной трапеции: трапеция может быть вписана в окружность в том и только в том случае, когда она равнобедренная.

Свойства описанной трапеции. Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.

Полезные следствия того, что в трапецию вписана окружность:

1. Высота описанной трапеции равна двум радиусам вписанной окружности.

2. Боковая сторона описанной трапеции видна из центра вписанной окружности под прямым углом.

Первое очевидно. Для доказательства второго следствия необходимо установить, что угол COD прямой, что так же не составляет большого труда. Зато знание этого следствия позволяет при решении задач использовать прямоугольный треугольник.

Конкретизируем следствия для равнобедренной описанной трапеции :

Высота равнобедренной описанной трапеции есть среднее геометрическое оснований трапеции
h = 2r = √(ab).

Рассмотренные свойства позволят более глубоко познать трапецию и обеспечат успешность в решении задач на применение ее свойств.

Остались вопросы? Не знаете, как решать задачи на трапецию?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

www.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две - боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

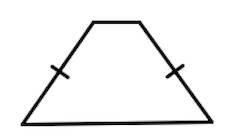
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

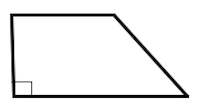
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

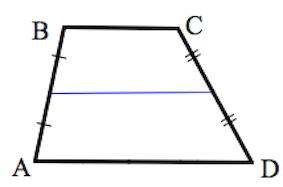
Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

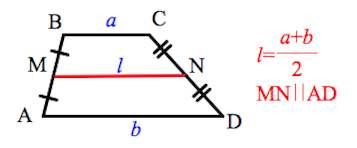
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

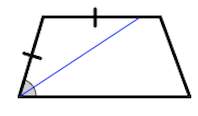
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

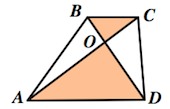
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

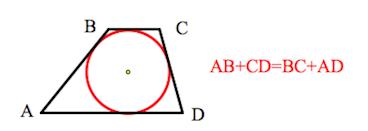
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

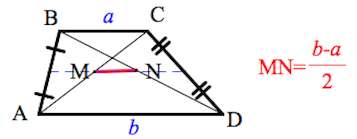
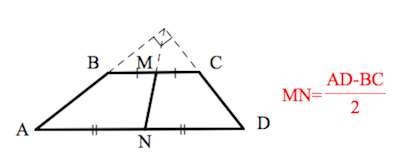
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

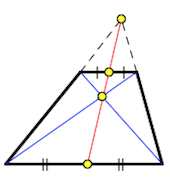
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

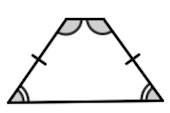
Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

Материалы по теме:

Карта сайта