Образовательный портал. Образование / Среднее образование и школа / Деление многочленов теорема безу схема горнера. Теорема Безу и следствие из нее. Корни многочлена

Деление многочленов теорема безу схема горнера. Теорема Безу и следствие из нее. Корни многочлена

07.08.2019

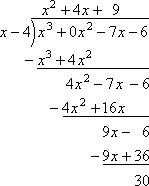
Найдем остаток от деления многочлена P (x ) на линейный двучлен вида (x ‑ a ), где a – некоторое число. Поскольку многочлен‑делитель имеет первую степень, остаток должен иметь нулевую степень, то есть представлять собою некоторое число r . Тогда если Q (x ) – многочлен-частное, то имеет место равенство: P (x ) = Q (x )·(x ‑ a ) + r . Подставив в полученное равенство вместо x число a , получим: P (a ) = Q (a )·(a ‑ a ) + r = Q (a )·0 + r = r . Таким образом, оказывается, что остаток от деления многочлена P (x ) на двучлен (x ‑ a ) можно найти, не выполняя деления, подставив в многочлен-делимое a вместо x . Доказанное утверждение, успешно применяемое при решении многих нестандартных задач, составляет суть теоремы Безу (Этье́нн Безу́, 1730 - 1783, французский математик, член Парижской академии наук).

Теорема остатка полезна для оценки многочленов при заданном значении х, хотя может показаться не таким, по крайней мере, сначала краснеть. Это объясняется тем, что инструмент представлен как теорема с доказательством, и вы, вероятно, не готовы к доказательствам на данном этапе ваших исследований. К счастью, вы не имеете «понять доказательство теоремы»; вам просто нужно понять, как использовать теорему.

Тогда теорема говорит о делении этого многочлена на некоторый линейный множитель х - а, где а - просто некоторое число.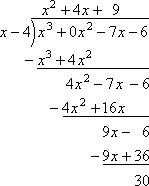

Вы знаете, из длинного разделения регулярных чисел, что ваш остаток должен быть меньше, чем все, что вы разделили. В полиномиальных терминах, поскольку мы делим на линейный множитель, тогда остаток должен быть постоянным значением.

Теорема Безу: Остаток r от деления многочлена P (x ) на двучлен (x ‑ a ) равен значению этого многочлена в точке a , т.е. r = P (a ).

Замечание 1: Многочлен называется приведенным , если его старший коэффициент (т.е. коэффициент при слагаемом наибольшей степени) равен 1. Например, многочлены , - приведенные, а , - нет.

В теореме остатка указывается связь между делением и умножением. Например, поскольку 12 ч 3 = 4, то 4 Ч 3 = 12. Если вы получаете остаток, вы делаете умножение, а затем добавляете остаток обратно. Этот процесс работает одинаково с полиномами. Но когда х = а, коэффициент «х - а» равен нулю!

Тогда оценка полинома от х = а дает нам. Что касается нашего конкретного примера. Вы правы, это было бы излишним. К счастью, это не то, что они действительно хотят от вас. Когда вы делите на линейный коэффициент, вы не имеете использовать длинное полиномиальное деление, вместо этого вы можете использовать синтетическое деление, которое намного быстрее.

Замечание 2: При делении многочлена с целыми коэффициентами на приведенный многочлен с целыми коэффициентами все коэффициенты многочлена-частного и многочлена-остатка оказываются также целыми (это легко понять, вспомнив, как выполняется деление многочлена на многочлен «уголком»). В частности, при делении многочлена с целыми коэффициентами на двучлен (x ‑ a ), где a – целое число, все коэффициенты многочлена-частного оказываются целыми.

Этот урок покажет вам, как интерпретировать фундаментальную теорему алгебры. Закончив этот урок, вы сможете изложить теорему и объяснить, что это значит. Прежде чем сформулировать теорему, рассмотрим следующую аналогию. Скажем, ваш банк взимает плату каждый раз, когда вы снимаете деньги с автомата. Если вы снимаете деньги пять раз в конкретный месяц, тогда вы ожидаете пять соответствующих банковских сборов в заявлении этого месяца. Давайте изменим это утверждение, используя некоторый математический язык.

Число a называется корнем многочлена P (x ), если P (a ) = 0 (другими словами, если число a – корень уравнения P (x ) = 0). Например, числа 1 и -1 являются корнями многочлена , числа -2 и 5 – корнями многочлена , а многочлен не имеет корней, поскольку невозможно выполнение равенства . Из теоремы Безу следует, что если число a является корнем многочлена P (x ), то остаток от деления многочлена P (x ) на двучлен (x ‑ a ) равен P (a ) = 0, то есть многочлен P (x ) делится на (x ‑ a ) без остатка. Другими словами, если a – корень многочлена P (x ), то P (x ) представим в виде: P (x ) = (x ‑ a )·Q (x ). Это утверждение составляет суть следствия из теоремы Безу.

Фундаментальная теорема алгебры

Основная теорема алгебры столь же проста, как и эта банковская аналогия. Обратите внимание, что термины «нули» и «корни» являются синонимами решений, используемых в контексте этого урока. Теперь мы уже должны знать, что полиномы могут быть описаны по их степени. Степень многочлена важна, потому что она говорит нам о числе решений многочлена.

Теорема не говорит нам, что такое решения. Это говорит только о том, сколько решений существует для данной полиномиальной функции. Прежде всего, важно понимать базовые концепции любых математических тем, которые вы изучаете. Кроме того, фундаментальная теорема алгебры имеет практическое применение. Например, если вам нужно найти решения полиномиальной функции, скажем, степени 4, вы знаете, что вам нужно продолжать работать, пока не найдете 4 решения.

Следствие из теоремы Безу: Число a является корнем многочлена P (x ) тогда и только тогда, когда P (x ) делится на (x ‑ a ) без остатка.

Задачи:

1. Найдите остаток от деления многочлена на .

2. Найдите многочлен третьей степени, который при делении на x дает остаток 1, на x ‑ 2 – остаток 3, а на делится без остатка.

Важно отметить, что теорема говорит о комплексных решениях, поэтому некоторые решения могут быть мнимыми или иметь мнимую часть. Может быть, нам следует сделать быстрый обзор сложных чисел. Поэтому все вещественные числа являются комплексными числами. Давайте рассмотрим несколько примеров.

Прежде чем мы рассмотрим некоторые примеры полиномиальных функций, давайте проясним понятие повторяющихся решений. Многочлена имеет многократные решения, если она имеет повторяющиеся множители. Пусть теперь функция равна нулю: 0 =. Если любой из трех факторов равен нулю, то функция равна нулю. В факторизованной форме эта функция равна. Вы могли заметить, что мнимые решения являются сопряженной парой. На самом деле мнимые решения полиномиальных функций, имеющих вещественные числа для коэффициентов, всегда встречаются в сопряженных парах.

3. Докажите, что многочлен делится на .

4. При каких значениях a и b многочлен делится без остатка на следующие многочлены:

5. При делении многочлена на x ‑ 1 в остатке получается 2, а при делении на x ‑ 2 - 1. Каков остаток от деления этого многочлена на ?

График этой функции показан ниже. Давайте также посмотрим на график функции. Это должны быть единственные решения, поскольку функция имеет определенную степень. Давайте посмотрим на график этой функции. Несмотря на то, что один и тот же фактор возникает дважды, он все еще создает два решения для этой функции. Другими факторами, очевидно, являются сопряженная пара мнимых факторов, как и ожидалось. Наши четыре решения заключаются в следующем.

Основная теорема алгебры просто утверждает, что число комплексных решений полиномиальной функции равно степени полиномиальной функции. Знание этой теоремы дает вам хорошую отправную точку, когда вам необходимо найти факторы и решения полиномиальной функции. Кроме того, не забудьте об использовании графиков полиномиальных функций, которые помогут вам. Графики также могут свидетельствовать о повторных решениях.

6. Найдите остаток от деления многочлена на .

7. Известно, что остаток от деления многочлена на равен 2x + 1. Найдите остаток от деления этого многочлена на:

а) x – 1;

б) 3x + 2;

8. Найдите приведенный многочлен четвертой степени, если известно, что он делится без остатка на , а при делении на дает в остатке .

Как только вы успешно пройдете этот урок, вы сможете. Понимание фундаментальной теоремы алгебры Отображение вашего понимания повторяющихся решений и комплексных решений Применим теорему при решении полиномиальных функций. Однако вопрос остается пульсирующим: каковы уравнения, решения которых выражаются радикалами?

Абель показал, что уравнение степени 5 не радикализировано. Этот результат звучит как смертельный звон для алгебры как искусство решения уравнений? Альгих не сказал своего последнего слова! Галуа указывает: Он ничего не оставил в общем обсуждении проблемы, которая нас оккупировала. Потому что раз и навсегда, что наша теория имеет замечательный, в любом случае можно ответить «да» или «нет». По следам Лагранжа Галуа интересует связь между решениями уравнения и перестановками решения, которые поддерживают эти отношения.

9. Какими могут быть остатки от деления многочлена P (x ) на x – 1, а многочлена Q (x ) – на x + 1, если при делении на x 2 – 1 многочлена в остатке получается -6?

10. Докажите, что число делится на 7.

11. Докажите, что остатки от деления на 11 чисел 100.000 и 1.000.000.000 равны.

12. Найдите остаток от деления числа на 26.

Галуа показывает, что если число этих подстановок может быть достаточно уменьшено, то уравнение разрешимо радикалами. Чтобы достичь этого великого результата, Галуа объединяет работы Лагранжа по разрешению уравнений и уравнения Коши на «группах» подстановок в непогрешимой и сильной теории, дающей условия разрешимости уравнений радикалами.

Мемуар о Галуа, который остается для нас, озаглавленный «Меморандум об условиях разрешимости уравнений радикалами», датирован 16 января. Он написан на трех двойных листах очень большого формата, которые объединены и сшиты вместе составляют десяток страниц.

13. Один из корней уравнения равен 3. Найдите значение параметра a и решите уравнение.

Гал.: стр. 111, №9.10 (б).

Домашнее задание:

14. Не выполняя деления, найдите остаток от деления многочлена на x + 2.

Этьен Безу–

Этот лист, без сомнения, служил для классификации отчета с его приема в Академии. Когда он восстанавливает рукопись, Галуа покрывает нижнюю часть этого листа различными знаками, вычислениями и О! Херувины, которые академики вряд ли оценят. Это сложное и плотное заявление требует некоторого объяснения используемых терминов, даже для адресатов статьи. Таким образом, Галуа продолжает свое изложение, вспоминая «определения и ряд известных нам лемм». Он уточняет: «Я слишком легко опускаю демонстрации».

Чтобы объяснить решения уравнения, математики привыкли разлагать его на произведение многочленов первой степени; для того чтобы этот продукт исчезал, необходимо и достаточно, чтобы один из многочленов обращался в нуль, т.е. интерес разложения. Однако, в зависимости от области определения, которая была связана с уравнением, это разложение не всегда возможно: арабские математики, как мы видели, принимали только положительные решения.

французский математик, член Парижской Академии Наук(с 1758 года), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года.

С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.

Основные работы Этьена Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений. В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную К. Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках. Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный“Курс математики “, написанный им в 1764-69 годах. Безу развил метод неопределённых множителей, в элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе. Часть трудов Безу посвящена внешней баллистике. Именем учёного названа одна из основных теорем алгебры.

Они могли бы разложить это уравнение только в виде =. Такое уравнение, также называемое «неприводимым уравнением первой степени», является уравнением, которое не допускает рациональных делителей, т.е. не разбивается на произведение многочленов с рациональными коэффициентами. С другой стороны, уравнение, допускающее рациональные делители, приводимо.

Галуа объясняет: «Когда уравнение имеет все свои численные и рациональные коэффициенты, это просто означает, что уравнение можно разложить на множители, которые имеют их численные и рациональные коэффициенты». Затем Галуа указывает, что он обычно понимает под «рациональным». Его определение охватывает множество рациональных чисел и позволяет расширять. Удобно рассматривать как рациональную любую рациональную функцию определенного числа детерминированных величин, предположительно известных априори.

Теорема Безу.

Остаток от деления полинома Pn(x)

на двучлен (x-a) равен значению

этого полинома при x = a.

Пусть:

Pn(x) – данный многочлен степени n ,

двучлен (x-a) - его делитель,

Qn-1(x) – частное от деления Pn(x) на x-a (многочлен степени n-1) ,

R – остаток от деления (R не содержит переменной x как делитель первой степени относительно x).

Например, мы можем выбрать некоторый корень целого числа и считать рациональной любую рациональную функцию этого радикала. Когда мы соглашаемся выглядеть так, как известно, из некоторых величин, мы скажем, что добавим их к уравнению, которое мы должны решить. Будем говорить, что эти величины добавляются к уравнению.

При этом мы будем называть рациональной любую величину, которая будет выражаться как рациональная функция коэффициентов уравнения и некоторого количества величин, примыкающих к уравнению и произвольно согласованных. Другими словами, величина «рациональна» по отношению к набору чисел, если эта величина выражается с помощью этих чисел и четырех элементарных операций. Например, величина 1 2√2 является «рациональной» по отношению к набору целых чисел, к которым мы имеем «присоединенные» √2: число √2 было добавлено к множеству целых чисел, а затем умножено на 2 и добавлено Количество 1 2√2 было построено с использованием двух операций Ґ и, а числа 1, 2 и √2, все элементы набора целых чисел, к которым мы имеем «присоединенные» √ С другой стороны, величина 3 √√2 не является рациональным в смысле Галуа, поскольку эта величина включает «незаконное» извлечение корней.

Доказательство:

Согласно правилу деления многочленов с остатком можно записать:

Pn (x) = (x-a)Qn-1(x) + R .

Отсюда при x = a:

Pn (a) = (a-a)Qn-1 (a) + R =0*Qn-1(a)+R=

Значит, R = Pn (a) , т.е. остаток от деления полинома на (x-a) равен значению этого

полинома при x=a , что и требовалось доказать.

Следствия из теоремы.

Следствие 1:

Остаток от деления полинома Pn (x)

В заключение, количество рационально по отношению к вещам, если оно выражается этими вещами и четырьмя операциями. Конечно, неприводимость уравнения зависит от множества чисел, на которых он работает. Галуа пишет так: Свойства и трудности уравнения могут быть совершенно разными в зависимости от прилагаемых к нему величин.

Например, добавление количества может привести к неприводимому уравнению. Сегодня понятие присоединенного количества служит для построения промежуточных тел между полями большого числа: множество рациональных чисел, множество действительных чисел и множество комплексных чисел. Понятие тела присуще теории Галуа, даже если оно не использует этот термин.

на двучлен ax+b равен значению

этого полинома при x = -b/a ,

т. е. R=Pn (-b/a) .

Доказательство:

Согласно правилу деления многочленов:

Pn (x)= (ax + b)* Qn-1 (x) + R .

Pn (-b/a) = (a(-b/a) + b)Qn-1(-b/a) + R = R. Значит, R = Pn (-b/a) , что и требовалось доказать.

Следствие 2:

Если число a является корнем

многочлена P (x) , то этот

многочлен делится на (x-a) без

Мы отрицаем это свойство также следующим образом: числа тела воспроизводятся рациональными операциями. Таким образом, очевидно, что нулевое число никогда не может стать знаменателем частного. Это определение ясное: любой набор чисел, который может добавлять, вычитать, умножать и делить, представляет собой поле чисел: поле чисел представляет собой набор, в котором выполняются четыре элементарные операции. Таким образом, множество целых чисел не является телом, потому что, например, деление 1 на 2 не дает целого.

Таким образом, четыре элементарные операции структурируют определенные множества чисел в тела. Между тем добыча корневой нимеи порождает понятие сложения, также называемое расширением Галуа. Этот набор должен содержать √2 и должен быть таким, чтобы сложения, вычитания, умножения и повторяющиеся деления элементов, один «остается» в этом наборе. Теорема Кронекера-Капелли используется для оценки числа решений системы уравнений, т.е. мы ответим на вопрос, существует ли в данной системе уравнений одно решение, бесконечность или отсутствие решений.

Доказательство:

По теореме Безу остаток от деления многочлена P (x) на x-a равен P (a) , а по условию a является корнем P (x) , а это значит, что P (a) = 0 , что и требовалось доказать.

Из данного следствия теоремы Безу видно, что задача решения уравнения P (x) = 0 равносильна задаче выделения делителей многочлена P , имеющих первую степень (линейных делителей) .

Следствие 3:

Если многочлен P (x) имеет

попарно различные корни

a1 , a2 , … , an , то он делится на

произведение (x-a1) … (x-an)

без остатка.

Доказательство:

Проведём доказательство с помощью математической индукции по числу корней. При n=1 утверждение доказано в следствии 2 . Пусть оно уже доказано для случая, когда число корней равно k , это значит, что P(x) делится без остатка на (x-a1)(x-a2) … (x-ak) , где

a1 , a2 , … , ak - его корни.

Пусть P(x) имеет k+1 попарно различных корней.По предположению индукции a1 , a2 , ak , … , ak+1 являются корнями многочлена, а, значит, многочлен делится на произедение (x-a1) … (x-ak) , откуда выходит, что

P(x) = (x-a1) … (x-ak)Q(x).

При этом ak+1 – корень многочлена P(x) , т. е. P(ak+1) = 0 .

Значит, подставляя вместо x ak+1 , получаем верное равенство:

P(ak+1) = (ak+1-a1) … (ak+1-ak)Q(ak+1) =

Но ak+1 отлично от чисел a1 , … , ak , и потому ни одно из чисел ak+1-a1 , … , ak+1-ak не равно 0 . Следовательно, нулю равно Q(ak+1) , т. е. ak+1 – корень многочлена Q(x) . А из следствия 2 выходит, что Q(x) делится на x-ak+1 без остатка.

Q(x) = (x-ak+1)Q1(x) , и потому

P(x) = (x-a1) … (x-ak)Q(x) =

=(x-a1) … (x-ak)(x-ak+1)Q1(x) .

Это и означает, что P(x) делится на (x-a1) … (x-ak+1) без остатка.

Итак, доказано, что теорема верна при k =1 , а из её справедливости при n = k вытекает, что она верна и при n = k+1. Таким образом, теорема верна при любом числе корней, что и требовалось доказать.

Следствие 4:

Многочлен степени n имеет не более

n различных корней.

Доказательство:

Воспользуемся методом от противного: если бы многочлен Pn(x) степени n имел бы более n корней - n+k (a1 , a2 , … , an+k - его корни) , тогда бы по ранее доказанному следствию 3 он

бы делился на произведение (x-a1) … (x-an+k) , имеющее степень n+k , что невозможно.

Мы пришли к противоречию, значит наше предположение неверно и многочлен степени n не может иметь более, чем n корней, что и требовалось доказать.

Следствие 5:

Для любого многочлена P(x)

и числа a разность

(P(x)-P(a)) делится без

остатка на двучлен (x-a) .

Доказательство:

Пусть P(x) – данный многочлен степени n , a - любое число.

Многочлен Pn(x) можно представить в виде: Pn(x)=(x-a)Qn-1(x)+R ,

где Qn-1(x) – многочлен, частное при делении Pn(x) на (x-a) ,

R – остаток от деления Pn(x) на (x-a) .

Причём по теореме Безу:

R = Pn(a) , т.е.

Pn(x)=(x-a)Qn-1(x)+Pn(a) .

Pn(x) - Pn(a) = (x-a)Qn-1(x) ,

а это и означает делимость без остатка (Pn(x) – Pn(a))

на (x-a) , что и требовалось доказать.

Следствие 6:

Число a является корнем

многочлена P(x) степени

не ниже первой тогда и

только тогда, когда

P(x) делится на (x-a)

без остатка.

Доказательство:

Чтобы доказать данную теорему требуется рассмотреть необходимость и достаточность сформулированного условия.

1.Необходимость.

Пусть a – корень многочлена P(x) , тогда по следствию 2 P(x) делится на (x-a) без остатка.

Таким образом делимость P(x) на (x-a) является необходимым условием для того, чтобы a являлось корнем P(x) , т.к. является следствием из этого.

2.Достаточность.

Пусть многочлен P(x) делится без остатка на (x-a),

тогда R = 0 , где R – остаток от деления P(x) на (x-a) , но по теореме Безу R = P(a) , откуда выходит, что P(a) = 0 , а это означает, что a является корнем P(x) .

Таким образом делимость P(x) на (x-a) является и достаточным условием для того, чтобы a являлось корнем P(x) .

Делимость P(x) на (x-a) является необходимым и достаточным условием для того, чтобы a являлось корнем P(x) , что и требовалось доказать.

Многочлен, не имеющийй действи-

тельных корней, в разложении

на множители линейных множителей

не содержит.

Доказательство:

Воспользуемся методом от противного: предполо-жим, что не имеющий корней многочлен P(x) при разложении на множители содержит линейный множитель (x – a):

P(x) = (x – a)Q(x),

тогда бы он делился на (x – a) , но по следствию 6 a являлось бы корнем P(x) , а по условию он корней не содержит. Мы пришли к противоречию, значит наше предположение неверно и многочлен,

не имеющий действительных корней, в разложении на множители линейных множителей не содержит, что и требовалось доказать.

На основании теоремы Безу и следствия 5 можно доказать следующие утверждения:

1. Разность одинаковых натуральных степеней на разность их оснований делится без остатка:

Пусть P(x) = x n , P(a) = a n ,

тогда x n – a n – разность одинаковых натуральных степеней.

По следствию 5

P(x) - P(a) = x n – a n = (x – a)Q(x) ,

а это значит, что

(x n –a n)/(x–a)=Q(x), т.е. разность одинаковых натуральных степеней на разность их оснований делится без остатка, что и требовалось доказать.

(x n – a n)/(x – a) = x n-1 + ax n-2 + a 2 x n-3 + … +a n-2 x + a n-1 .

Материалы по теме: