Элементарные построения циркулем и линейкой. Из истории геометрического построения циркулем и линейкой. Подготовка учащихся к восприятию нового материала

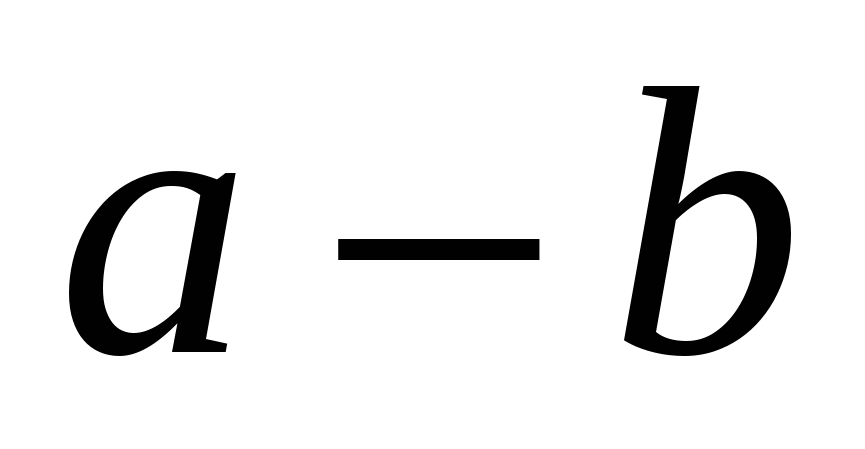
Задачи на построение циркулем и линейкой в 7 классе

Шувалова Ю.Г. – учитель математики МОУ школы №10 г.о. Тольятти

Задачи на построение циркулем и линейкой и сегодня считаются математически весьма интересными. Уже более ста лет это традиционный материал школьного курса геометрии. Одной из самых ценных сторон таких задач является то, что они развивают поисковые навыки решения практических проблем, приобщают к самостоятельным исследованиям, способствуют выработке конкретных геометрических представлений. Задачи на построение вызывают интерес, способствуют активизации мыслительной и познавательной деятельности. При их решении активно используются знания о свойствах фигур, совершенствуются навыки геометрических построений. В результате развиваются конструктивные способности, что является одной из целей изучения геометрии.

Круг задач, рассматриваемых в геометрии, очень широк. Среди них особое место занимают задачи на построение, которые способствуют развитию определенности, последовательности и обоснованности мышления. На этих задачах можно научиться таким методам познания, как анализ и синтез.

Структура решения задачи на построение.

Решение задач на построение с помощью циркуля и линейки, состоит не в том, чтобы выполнить соответствующие построения, а в том, чтобы найти алгоритм решения, то есть, описать решение задачи в виде последовательности уже известных стандартных построений. Правильное, осмысленное решение задач на построение состоит из основных этапов: анализ, построение, доказательство (синтез), исследование.

Анализ. Составляется план решения. Для этого поступают так: предполагают задачу решенной, делают от руки примерный чертеж искомой. Нужно найти такую зависимость между данными и искомыми величинами, которая позволила бы определить положение искомой точки (отрезка или угла), на нахождение которых нацелено решение задачи.

Построение – механическое выполнение тех приемов, которые были выведены из плана решения задачи, т.е. анализа. При построении используют основные приемы (задачи на построение), т.е. любая задача на построение разбивается на конечное число шагов (простейших задач на построение).

Доказательство. Когда искомая фигура построена, необходимо доказать, что она удовлетворяет всем требованиям задачи. При этом ход рассуждений будет обратный тому, который применялся при анализе. Поэтому иногда доказательство называют синтезом.

Исследование имеет целью выяснить, всегда ли задача разрешима, сколько решений допускается (одно или несколько). Необходимо рассмотреть всевозможные частные случаи, причем нужно выяснить, меняется ли ход решения в них и как именно.

Основные построения с помощью циркуля и линейки.

Для выполнения основных построений с помощью циркуля и линейки используется метод решения, при котором искомую точку строят как точку пересечения множеств (геометрических мест), определяемых некоторыми условиями. Данный метод так и называется – метод пересечения множеств или метод геометрических мест . С помощью этих инструментов мы можем выполнить огромное множество построений. Какие простейшие построения являются стандартными? Авторы учебников , к основным построениям в 7 классе относят:

построить отрезок, равный данному отрезку; построить середину отрезка.

построить перпендикуляр к прямой, построить серединный перпендикуляр.

построить угол, равный данному углу; построить биссектрису угла.

построить треугольник (по трём сторонам, по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по двум сторонам и углу, противолежащему одной из сторон).

Перед использованием топографической карты проверьте информацию о типе сетки на краю! В зависимости от масштаба топографической карты поверните координированный прибор, чтобы иметь прямые, используемые надписи. Найденная точка находится в углу. . Клинометр представляет собой соотношение, которое служит для указания наклона местности на основе расстояния между изоипсом. Транспортер имеет 5 различных наклонов от 10 ° до 50 ° с интервалом 10 °.

Чтобы получить указание на склоне, просто сравните изоипс с расстоянием между вырезами. Каждый наклон имеет пять выемок, чтобы можно было сравнивать до 5 изоипсов за раз. Существенным является наклон 30 °, выше которого резко увеличивается риск лавин.

построить прямоугольный треугольник (по гипотенузе и катету, по гипотенузе и острому углу).

построить прямую, проходящую через данную точку параллельно данной прямой

К стандартным построениям 7 класса добавим:

1. Построение отрезков ,

,

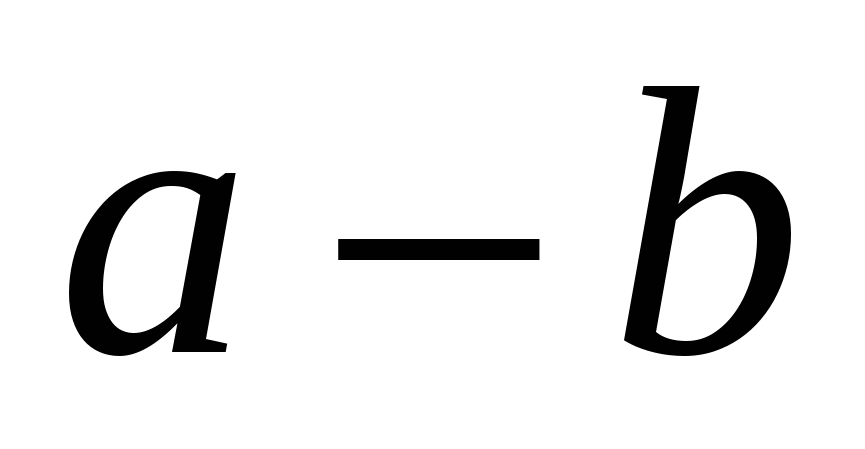. Изобразим луч ОС и отрезки а и b (а > b ). Затем циркулем построим окружность радиуса а с центром О (Приложение 1, рис. 1.1). Эта окружность пересечет луч ОС в некоторой точке К, затем циркулем построим окружность радиуса b с центром К и получим точку пересечения Р на продолжении луча ОС и точку Н на отрезке ОК. При этом ОР= ОК + КР = а + b , ОН= ОК – КН = а – b . Изобразим луч ОС и отрезок АВ = а. Затем циркулем построим окружность радиуса АВ с центром О. Эта окружность пересечет луч ОС в некоторой точке А 1 . На продолжении луча ОС от точки А 1 построим окружность радиуса АВ с центром А 1 – получим точку А 2 (при этом ОА 2 = 2АВ). Построение будем продолжать до тех пор, пока ОА n = n а. (Приложение 1, рис. 1.2).

2. Построение углов

,

. Циркулем и линейкой строим

МОК=. Строим

КОР= так, чтобы луч ОР проходил внутри

МОК, и

ЕОК= так, чтобы луч ОЕ проходил вне

МОК. При этом получаем:

МОЕ=

,

МОР=

(Приложение 1, рис. 2).

3. Построение угла в n раз больше данного угла. Построение угла в n раз больше данного угла сводится к построению n раз угла, равному данному. Например: чтобы построить

MON в 3 раза больше заданного угла АВС, необходимо построить

МОК=

АВС. Затем построить

КОР=

АВС, потом

РОN =

АВС. При этом получим

MON =

МОК +

КОР +

РОN = 3

АВС.

4. Трисекция угла. Искусство построения геометрических фигур при помощи циркуля и линейки было в высокой степени развито в Древней Греции. Знаменитой была в древности задача о трисекции угла (о разделении угла на три равные части с помощью циркуля и линейки). Любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Попытки решения задачи с помощью инструментов и средств были предприняты еще в V в. до н.э. Французский математик П. Ванцель в 1837г. первым строго доказал, что невозможно осуществить трисекцию циркулем и линейкой. Задача о трисекции угла оказывается разрешимой и при некоторых других частных значениях угла: 90 0 , 45 0 , 135 0 (приложение 2). Деление прямого угла на три равные части умели производить ещё пифагорейцы, основываясь на том, что в равностороннем треугольнике каждый угол равен 60 о.

5. Деление данного угла на

равных углов. Построение биссектрисы угла позволяет разделить любой угол на 2, 4, 8, … 2 n равных углов. В каждом случае задача сводится к построению биссектрис полученных углов, что выполнимо всегда циркулем и линейкой. Например, разделить угол АВС на 4 равных угла. Строим биссектрису ВК

АВС, получаем

АВК=

СВК=

АВС:2. Строим биссектрисы ВР и ВМ углов

АВК и

CDR соответственно. Получаем:

АВР=

РВК=

МВК=

СВМ=

АВК:2=

АВС:4.

Возникает вопрос: Можно ли разделить произвольный угол на 5, 7, 11, … равных углов? Данная задача оказывается разрешимой при некоторых частных значениях угла. Например: циркулем и линейкой можно выполнить следующие построения (при условии, что заданные углы уже построены и их величина известна):

Задача 1: Построить углы, равные 66 0: 11=6 0 , 50 0: 5=10 0 . Для решения этих задач воспользуемся углом 60 0 – равносторонним треугольником. В первой задаче получаем 66 0 –60 0 = 6 0 , строим дважды по углу 6 0 (60 0 –6 0 –6 0 = 48 0), затем делим угол 48 0 на

равных углов (т.е. проводим биссектрисы). Рассуждая также, получаем во второй задаче 1) 60 0 –50 0 = 10 0 , 2) 50 0 –10 0 = 40 0 , 3) 40 0: 4=10 0 ;

Задача 2: Построить угол 53 0 , если построен угол 104 0 . При решении используем построения прямого угла, биссектрисы угла и угла 60 0 . Построение: 1) 104 0 –90 0 =14 0 , 2) 14 0: 2 = 7 0 , 3) строим 60 0 и 60 0 –7 0 =53 0 .

Вывод: рассматривая построения 4 и 5, задачи 1 и 2 всегда можно построить:

1) прямой угол, углы: 60 0 , 30 0 , 45 0 , 15 0 .

2) можно разделить некоторые заданные углы на данное количество равных углов или построить угол необходимой величины.

3) задачи 1, 2 или подобные им можно использовать на кружках, в олимпиадах или во внеклассных мероприятиях.

3. Задачи на построение циркулем и линейкой.

Анализ олимпиадных заданий для 7 класса, проводимых в городе Тольятти, и, предложенных для подготовки к олимпиадам в различных источниках, показал, что задачи на построение среди них отсутствуют. Предлагаю задачи, которые могут быть использованы для подготовки к олимпиаде по математике или для проведения олимпиад в 7 классе, так как дадут возможность ученикам показать не только свои знания геометрического материала, но и умение анализировать, логически мыслить и проявлять изобретательность в решении задач.

Задача 1: Постройте прямоугольный треугольник по гипотенузе и углу между ней и проведенной к ней медианой. Сначала рассмотрим задачу: На отрезке AB как на диаметре построена окружность. Докажите, что из всех точек окружности, отличных от A и B, отрезок AB виден под прямым углом.

Решение: АОС и ВОС – равнобедренные, т.к. радиусы ОА=ОВ=ОС.

АОС и

СОВ смежные углы, тогда

СОВ = 180 0 -

АОС. По свойству углов равнобедренного треугольника и по теореме о сумме углов треугольника получаем:

САО=

АСО= (180 0 –

АОС): 2= 90 0 –

АОС:2,

ОВС=

ОСВ= (180 0 –

СОВ) : 2 = (180 0 – (180 0 –

АОС)) : 2 =

АОС: 2.

АСВ =

АСО +

ОСВ =90 0 –

АОС: 2 +

АОС: 2 = 90 0 . Вернемся к решению задачи.

Анализ: Пусть АВС (

ВАС = 90 0 , ВС = а, АК – медиана,

АКС =) – искомый. Точки А, В, С лежат на окружности с центром в К радиуса ВК, т.к.

ВАС = 90 0 опирается на диаметр ВС (доказано в предыдущей задаче).

Построение: Строим ВС = а, К – середину ВС. Строим

МКС =

АКС = . Строим А – точку пересечения луча КМ и окружности с центром в К радиуса ВК.

Доказательство: Пусть АВС– искомый, т.к. ВС = а, ВК=КС (по построению),

ВАС = 90 0 (опирается на диаметр окружности), АК – медиана,

АКС =.

Исследование: Решение сводится к построению отрезка, равного данному, середины отрезка и угла, равного данному. Данные построения выполнимы всегда.

Задача 2: Дан угол и точка внутри него. Постройте отрезок с концами на сторонах угла и серединой в этой точке.

А

нализ: Дан

ЕАР и точка М внутри угла. Пусть ВС искомый отрезок, удовлетворяющий условиям задачи: ВМ=МС, ВАЕ, САР. Проведем АМ, откладываем на его продолжении отрезок МК=АМ. АМВ = КМС (по I признаку). У них:

ВМА=

КМС (вертикальные), АМ=МК, ВМ=МС. Следовательно,

ВАМ=

МКС. Значит, построение ВС сводится к построению точки С на АР, т.е. к построению АК=2АМ и

МКС=

ВАМ.

Построение: Проводим луч АМ, откладываем на его продолжении МК=АМ. Строим

МКС=

ЕАК. Получаем С на стороне АР

ЕАР. Проводим луч СМ, получаем В на луче АЕ. Отрезок ВС – искомый.

Доказательство: При построении получаем АМВ = КМС (по II признаку). У них:

ВМА=

КМС (вертикальные), АМ=МК (по построению),

ВАМ=

МКС (по построению). Следовательно, ВМ=МС. Получаем ВС – искомый отрезок.

Исследование: Построение выполнимо всегда, т.к. сводится к построению отрезка, равного данному, и угла, равного данному.

Задача 3. Дана прямая, на которой лежит биссектриса угла A треугольника ABC. По разные стороны от этой прямой даны две точки – основания: а) медиан; б) высот, проведенных из вершин B и C. Восстановите треугольник ABC.

Анализ: Пусть АВС (луч АО – биссектриса

А, медианы СN , ВМ) – искомый. Проведу ММ 1 ||АО и NN 1 ||АО. АКМ= АКМ 1 (АРN = АРN 1) (по II признаку). У них: 1) АК (АР) – общая, 2)

АКМ=

АКМ 1 =90 0 (

АРN =

АРN 1 =90 0), 3)

КАМ=

КАМ 1 – АО биссектриса

А. Получаю, что точки М, М 1 лежат на АС, N , N 1 лежат на АВ и находятся на одном расстоянии от АО. Аналогично, если точки N , М – основания высот.

Построение: Строю МКАО и N РАО. Откладываю КМ 1 =КМ и РN 1 =РN . Провожу прямые МN 1 иN М 1 , получаю А на пересечении АО, МN 1 иN М 1 . а) Откладываю МС=АМ и N В=АN . б) Строю МВАМ (В – точка пересечения МВ и АВ), N СN А (С – точка пересечения N В и АМ). Провожу ВС. АВС построен.

Доказательство: В обоих случаях мы получаем: точки М и М 1 лежат на АС, N и N 1 лежат на АВ. АКМ= АКМ 1 (по I признаку). У них: 1) АК – общая, 2)

АКМ=

АКМ 1 =90 0 , 3) КМ= КМ 1 – по построению.



КАМ=

КАМ 1

АО биссектриса

А. а) точки N , М – основания медиан, т.к. по построению МС=АМ и N В=АN . б) точки N , М – основания высот, т.к. по построению МВАМ, N СN А.

Исследование: задача не имеет решения, если точки N , М находятся на одном расстоянии от АО. При этом МN 1 ||AO , N М 1 ||AO

МN 1 ||N М 1

точку А построить невозможно.

В следующих задачах приведем только анализ или/и построение.

Задача 4: Постройте треугольник по трем медианам.

А

нализ: Пусть АВС (медианы СN = р, ВМ = n , АК = m ) – искомый. Строим АCP = АВС: АР=ВС, РС=АВ, ОС=АК=m . Проводим N О. NO – средняя линия ABP

NO = ВР:2= ВМ (по свойству средней линии треугольника). Получаем NOC : СN = р, NO = n , ОС = m . На луче ON отложим NS =NO . Т.к. ВNS = АNO по I признаку. У них:

ВNS =

АNO как вертикальные, NS =NO по построению, АN =N В (N С – медиана). Значит, S В= ВК= КС= СS :3.

Построение: Строим NOC : СN = р, NO = n , ОС = m . На луче ON отложим NS =NO . Проводим СS , строим точку В:

. Проводим луч ВN , откладываем АN = ВN . АВС – искомый.

Задача 5. Построить прямоугольный треугольник по гипотенузе с и сумме катетов .

Анализ: Пусть АВС (

А=90 0) построен. На луче ВА отложим отрезок AD = AC . Получим АD С – равнобедренный, в котором

(свойство внешнего угла треугольника). Задача сводится к построению ВСD по двум сторонам BD = b +c , ВС = а и

D =45 0 . Чтобы получить точку А, достаточно провести СА D В.

Задача 6. Постройте треугольник по данной стороне, углу, к ней прилежащему, и сумме двух других сторон.

А

нализ: Пусть АВС – искомый. На продолжении ВА отложу AD =CA . Соединю C и D . В CBD имею: BD = b +c , BC = a , СBD = B . CBD можно построить по двум сторонам и углу между ними. CAD – равнобедренный: АН – высота, медиана. Проведя серединный перпендикуляр АН CD , определю вершину А.

Задача 7. Постройте треугольник по двум углам и периметру.

Анализ: Пусть АВС – искомый. На продолжении стороны АВ в обоих направлениях отложу отрезки DA = АС и ВЕ = СВ и соединю D с С и Е с С, получу DCE , в котором DE = Р. Треугольники DAC и ВЕС – равнобедренные, и АК DC , где DK = KC и BF FE , что позволит определить вершины А и В.

,

(свойство внешнего угла треугольника). Задача сводится к построению DCE по стороне DE =Р и

D ,

E .

Пятиконечная звезда - наиболее почитаемый символ у всех народов мира во все времена. Ее изображения обнаружены у самых истоков цивилизации, когда еще не была изобретена письменность.

Самое первое изображение пятиконечной звезды, найденное археологами, датируется 3500 годом Она была запечатлена на глиняной табличке, найденной при раскопках шумерского города Урук.

Символ звезды пользовался популярностью в Древнем Египте и Вавилоне. Его почитали древние римляне и греки, считая пятиконечную звезду символом круговорота в природе. Пять углов звезды греки ассоциировали с пятью элементами, из которых сотворен наш мир, - землей, водой, воздухом, огнем и эфиром.

Является атрибутом гербов и флагов многих современных государств и присутствует на воинских знаках различия.

А вот нарисовать эту незамысловатую фигуру не так просто, как может показаться на первый взгляд.

Как нарисовать пятиконечную звезду, не отрывая карандаш от бумаги

Великий греческий мыслитель и математик Пифагор называл пятиконечную звезду математическим совершенством. Действительно, эту сложную фигуру можно нарисовать одной ломаной линией, не отрывая карандаша от листа бумаги и вернувшись в конце в ту же отправную точку, с которой был начат рисунок.

Вот такая она, сложная и простая на первый взгляд фигура - пятиконечная звезда. Как нарисовать ее одной ломаной линией, видно из рисунка.

используя линейку и транспортир

Теперь узнаем, как нарисовать правильную пятиконечную звезду. Из измерительных приборов понадобятся линейка и транспортир.

Чтобы получилась звезда, нужно провести отрезки одинаковой длины таким образом, чтобы внутренние углы между всеми пятью вершинами фигуры были равны 36°. Практически это осуществляется следующим образом - чертится угол в 36°, от его вершины отмеряются отрезки одинаковой длины, и от их конечных точек проводятся новые прямые под углом 36°.

Можно также подойти к решению задачи немного иным способом, нарисовав равносторонний пятиугольник с вершинами углов в 106°, а затем соединив отрезками его противолежащие углы.

Если вы соблюдете все условия, у вас в конечном счете получится красивая пятиконечная звезда. Как нарисовать ее более простым способом, читайте далее.

Как нарисовать звезду с помощью циркуля и транспортира

Теперь вам понадобятся циркуль и транспортир. Так как в окружности 360°, то в 1/5 ее части - 72° (360: 5 = 72). Приступаем к построению.

Начертите с помощью циркуля окружность. Отметьте на ней отправную точку - вершину звезды и середину окружности. Возьмите транспортир, совместите его центр с центром окружности, и по всей отметьте рисками будущие точки вершин звезды через каждые 72°.

Останется соединить их прямыми, и получится красивая пятиконечная звезда. Как нарисовать ее, если под рукой не окажется транспортира? Без него можно обойтись, из инструментов понадобится лишь линейка и циркуль.

Как нарисовать звезду с помощью циркуля и линейки

Как нарисовать пятиконечную звезду циркулем? Рассмотрим вариант 1.

Чертим окружность. Измеряем ее диаметр с помощью линейки. Производим несложные математические действия: умножаем на коэффициент 0,58779. Полученный результат - необходимая (прямой, соединяющей 2 точки кривой линии, а в нашем случае - окружности), с помощью которой мы сможем разделить окружность на 5 равных частей.

Например, диаметр окружности равен 7 см. Умножаем 7 х 0,58779 = 4,11453, округляем до десятых (так как нарисовать на бумаге отрезок более точной длины не представляется возможным), получим 4,1 см. Это и будет нужная длина хорды.

Осталось раздвинуть и зафиксировать ножки циркуля на данную величину, и можно делать насечки на окружности. Когда вы их соедините, получится пятиконечная звезда.

Как нарисовать фигуру другим способом? Рассмотрим вариант 2.

Для начала начертим вписанный в окружность. Как нарисовать правильную пятиконечную звезду на его основе, показано на рисунке 2.

Начертите циркулем окружность. Условно обозначим ее центр как О. Через точку О проведите прямую - диаметр нашей окружности. Прочертите радиус этой окружности таким образом, чтобы он был перпендикулярен диаметру. Точку пересечения радиуса с окружностью обозначим как V. Слева от точки О отложите расстояние, равное половине длины радиуса этой окружности, обозначьте его точкой А. Из точки А через точку V проведите полуокружность до пересечения с линией диаметра (на рисунке она выделена красным цветом) и обозначьте ее точкой В. Длина отрезка VB и будет длиной хорды, с помощью которой окружность разделится на 5 равных частей. Останется лишь соединить полученные точки в виде звезды.