Свойства ромба параллелограмма трапеции. Тема урока: «Параллелограмм, прямоугольник, ромб, квадрат и их свойства, формулы для вычисления их площадей». Определение и свойство ромба

Тема урока: «Параллелограмм, прямоугольник, ромб, квадрат и их свойства, формулы для вычисления их площадей».

Цель: систематизация знаний по теме “Четырехугольники”.

Много ль времени, аль мало С той поры уж пробежало За горами, за лесами, За широкими морями,Против неба – на земле Жил старик в одном селе.Четырехугольником он звался, Род великий начинался С старика того. Так вот.У старинушки два сынаВсе в отца, да вот причина: Был один из них горбат,А другой “пузоковат”.Кто такие эти детиМожет знает кто на свете?

Четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.

Время катит чередом, Час за часом, день за днём,- Прибавляя с каждым годом, Разрослась семья народом.

Справочник Меню

Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны Свойства параллелограмма Признаки параллелограмма Площадь параллелограмма Частные виды параллелограмма: прямоугольник и ромб AB || CD BC || AD

Свойства параллелограмма В параллелограмме противоположные стороны равны и противоположные углы равны. 2. Диагонали параллелограмма точкой пересечения делятся пополам. AB = CD BC = AD AО = ОC BО = ОD

Признаки параллелограмма Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм. 3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. BC || AD BC = AD AО = ОC BО = ОD BC = AD АB = СD

Площадь параллелограмма ВН – высота параллелограмма AD - основание S = BH AD A D B C Н? S = AB AD sin ?

Справочник Меню

Ромб – это параллелограмм, у которого все стороны равны BC|| AD, AB || CD AB = BC = CD = AD Свойства ромба Площадь ромба

Свойства ромба В ромбе противоположные углы равны. 2. Диагонали ромба точкой пересечения делятся пополам, взаимно перпендикулярны и делят углы ромба пополам L А = L С, L В = L D AО = ОC, BО = ОD AC + BD LBAO = LDAO, LABO = LCBO

Площадь ромба АН – высота ромба DС - основание S = АH DС А D O B C S = 1/2 АC BD

Справочник Меню

Прямоугольник – это параллелограмм, у которого все углы прямые. Свойства прямоугольника Признак прямоугольника Площадь прямоугольника Частный вид прямоугольника -квадрат AB || CD, BC || AD L А = L В = L С = L D = 90 о

Свойства прямоугольника В прямоугольнике противоположные стороны равны и противоположные углы равны. 2. Диагонали прямоугольника равны и точкой пересечения делятся пополам. AB = CD BC = AD BD = AC AО = ОC BО = ОD

Признак прямоугольника Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник BD = AC

Площадь прямоугольника S = АB AD

Справочник

Квадрат – это прямоугольник, у которого все стороны равны. Свойства квадрата Площадь квадрата AB || CD, BC || AD, AB = CD = BC = AD о L А = L В = L С = L D = 90

Свойства квадрата У квадрата все стороны равны и все углы равны. 2. Диагонали квадрата взаимно перпендикулярны, равны, точкой пересечения делятся пополам и делят углы квадрата пополам. AB = CD = BC = AD L А = L В = L С = L D = 90 AC + BD BD = AC AО = ОC, BО = ОD LBAO = LDAO, LABO = LCBO о

Площадь квадрата А В С D А В С D

Справочник

Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие не параллельны. BC || AD, AB || CD BC и AD – основания, AB и CD – боковые стороны Виды трапеции Средняя линия трапеции Площадь трапеции

Виды трапеции Равнобедренная - Прямоугольная - Произвольная боковые стороны равны один из углов прямой

Средняя линия трапеции Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон. MN- средняя линия М N Средняя линия трапеции параллельна основаниям и равна их полусумме MN || AD, MN || AD, MN = (BC + AD) / 2

Площадь трапеции ВН – высота трапеции ВС и AD - основания S = 1/2 BH (ВС + AD) H

Задачник задачник

Четырёхугольник Найдите углы выпуклого четырёхугольника, если они равны друг другу. Найдите углы выпуклого четырёхугольника, если они пропорциональны числам 1,2,4,5. Найдите стороны четырёхугольника, если его периметр равен 8 см, а одна сторона больше каждой из других сторон соответственно на 3 мм, 4мм и 5мм. Найдите стороны четырёхугольника, если его периметр равен 66 см, первая сторона больше второй на 8 см и на столько же меньше третьей стороны, а четвёртая в три раза больше второй. Докажите, что если не все углы выпуклого четырёхугольника равны друг другу, то хотя бы один из них тупой.

Параллелограмм Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если разность двух сторон равна 7 см. Найдите углы параллелограмма, если сумма противолежащих углов равна 142. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. На диагонали BD параллелограмма ABCD отмечены точки P и Q так, что PB = QD. Докажите, что четырёхугольник APCQ – параллелограмм. В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов. Докажите, что при их пересечении образуется прямоугольник.

Ромб Найдите периметр ромба ABCD, в котором L В = 60, АС= 10,5 см. Найдите углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 кв. см. Сторона ромба равна 24 см, а один из его углов 150 . Найдите расстояние между его противолежащими сторонами Из вершины В ромба ABCD, проведены перпендикуляры ВК и ВМ к прямым AD и DC. Докажите, что луч BD является биссектрисой LКВМ. о о

Прямоугольник Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольники АОВ и АОD равнобедренные. Биссектриса одного из углов прямоугольника делит большую сторону пополам. Найдите периметр прямоугольника, если его меньшая сторона 12 см. Стороны прямоугольника относятся как 2: 7. Найдите стороны прямоугольника, если его площадь равна 108 кв.см. Сторона прямоугольника равна 4 см и образует с диагональю угол 60. Найдите эту диагональ. Пол комнаты, имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина – 5 см. Сколько потребуется таких дощечек для покрытия пола? о

Квадрат Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину. 2. Диагональ квадрата 24 см. Найдите периметр четырёхугольника, образованного отрезками, последовательно соединяющими середины сторон данного квадрата. Сторону квадрата увеличили в 3 раза. Во сколько раз увеличилась его площадь? Площадь квадрата равна 18 кв.см. Найдите диагональ квадрата. В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а другие две – на катетах. Найдите сторону квадрата, если известно, что гипотенуза равна 12 см.

Трапеция Найдите углы B и D трапеции ABCD с основаниями AD и BC, если LА = 36 ,LС= 117 . Докажите, что трапеция равнобедренная, если её диагонали равны. Основания прямоугольной трапеции равны 10 см, 15 см, а один из углов – 45 .Найдите меньшую боковую сторону трапеции. Найдите площадь равнобедренной трапеции. Если её основания равны 16 см и 30 см, а диагонали взаимно перпендикулярны. Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линию трапеции о о о

Проверь себя

Задание № 1 Какое из утверждений неверное: квадрат является одновременно параллелограммом и прямоугольником; угол между стороной и диагональю квадрата равен 45 ; существует квадрат, который не является ромбом; диагонали квадрата взаимно перпендикулярны.

Задание № 2 Найдите площадь ромба, диагонали которого равны 26 см и 8 см: 208 кв.см; 104 кв.см; 52 кв.см; 68 кв.см

Задание № 3 В каком случае нельзя утверждать, что данная фигура – параллелограмм? а) б) в) г)

Задание № 4 Диагонали прямоугольника ABCD пересекаются в точке О. Определите периметр треугольника АВО, если АВ = 6 см, а диагональ прямоугольника равна 14 см: 19 см; 26 см; 20 см; 18 см

Задание № 5 Какое из утверждений неверное? у прямоугольника углы прямые, а у ромба не обязательно; у ромба диагонали взаимно перпендикулярны, а у прямоугольника не обязательно; у ромба диагонали являются биссектрисами его углов, а у параллелограмма не обязательно; у ромба диагонали равны, а у прямоугольника не обязательно;

Задание № 6 Какая из фигур не является прямоугольником? а) б) в) г)

Задание № 7 В прямоугольнике ABCD проведена биссектриса АМ. ВМ= 5см, МС =4 см. Найдите площадь прямоугольника: 36 кв. см 45 кв. см 28 кв. см 56 кв.см

Задание № 8 Найти площадь трапеции ABCD с основаниями AB и CD, если BC перпендикулярна AB, AB= 5 см, BC= 8 см, CD= 13 см. 144 кв.см; 36 кв.см; 72 кв.см; 70 кв.см

Задание № 9 Какое из утверждений неверное? параллелограмм, у которого диагонали взаимно перпендикулярны, является квадратом; прямоугольник, у которого все стороны равны, является квадратом; ромб у которого один угол прямой, является квадратом; ромб, у которого диагонали равны, является квадратом

Задание № 10 Найдите высоту параллелограмма, если его площадь равна 75,6 кв. см, а основание - 14 см. 23,8 см; 5,4 см; 61,6 см; 16 см.

Спасибо за работу!

По-вто-ре-ние тео-рии и ре-ше-ние задач

1. Определение, виды и свойства трапеции

Ранее мы уже по-зна-ко-ми-лись с та-ки-ми ви-да-ми че-ты-рех-уголь-ни-ков, как па-рал-ле-ло-грамм и тра-пе-ция, и их част-ны-ми слу-ча-я-ми - пря-мо-уголь-ни-ком, ром-бом и квад-ра-том. Мы изу-чи-ли их ос-нов-ные свой-ства и при-зна-ки. Се-год-ня мы по-вто-рим и обоб-щим все по-лу-чен-ные нами зна-ния по этой теме.

По-вто-рим ос-нов-ной тео-ре-ти-че-ский ма-те-ри-ал.

Тра-пе-ция - это че-ты-рех-уголь-ник, у ко-то-ро-го две про-ти-во-по-лож-ные сто-ро-ны па-рал-лель-ны, а две дру-гие не па-рал-лель-ны (см. Рис. 1).

Рис. 1. Тра-пе-ция

Вы-де-ля-ют два от-дель-ных типа тра-пе-ций: рав-но-бед-рен-ную и пря-мо-уголь-ную.

Рав-но-бед-рен-ная тра-пе-ция - это тра-пе-ция, в ко-то-рой бо-ко-вые сто-ро-ны равны (см. Рис. 2).

Рис. 2. Рав-но-бед-рен-ная тра-пе-ция

Пря-мо-уголь-ная тра-пе-ция - это тра-пе-ция, в ко-то-рой одна из бо-ко-вых сто-рон пер-пен-ди-ку-ляр-на ос-но-ва-нию (см. Рис. 3).

Рис. 3. Пря-мо-уголь-ная тра-пе-ция

От-дель-но стоит вспом-нить такой важ-ный эле-мент тра-пе-ции, как ее сред-няя линия.

Сред-няя линия тра-пе-ции - это от-ре-зок, со-еди-ня-ю-щий се-ре-ди-ны бо-ко-вых сто-рон тра-пе-ции (см. Рис. 4).

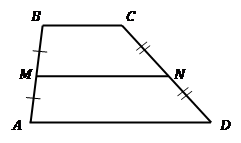
Рис. 4. Сред-няя линия тра-пе-ции

Ос-нов-ные свой-ства сред-ней линии тра-пе-ции :

1. - па-рал-лель-на ос-но-ва-ни-ям тра-пе-ции;

2. - равна их по-лу-сум-ме.

2. Определение, свойства и признаки параллелограмма

Па-рал-ле-ло-грамм - че-ты-рех-уголь-ник, у ко-то-ро-го каж-дые две про-ти-во-по-лож-ные сто-ро-ны па-рал-лель-ны (см. Рис. 5).

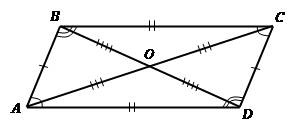
Рис. 5. Па-рал-ле-ло-грамм

Ос-нов-ные свой-ства па-рал-ле-ло-грам-ма :

Чтобы иметь воз-мож-ность при ре-ше-нии задач поль-зо-вать-ся ука-зан-ны-ми свой-ства-ми, нам необ-хо-ди-мо по-ни-мать, яв-ля-ет-ся ли ука-зан-ный че-ты-рех-уголь-ник па-рал-ле-ло-грам-мом или нет. Для этого необ-хо-ди-мо знать при-зна-ки па-рал-ле-ло-грам-ма.

Тео-ре-ма. Пер-вый при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке две про-ти-во-по-лож-ные сто-ро-ны равны и па-рал-лель-ны (см. Рис. 6), то этот че-ты-рех-уголь-ник - па-рал-ле-ло-грамм. па-рал-ле-ло-грамм.

Рис. 6. Пер-вый при-знак па-рал-ле-ло-грам-ма

Тео-ре-ма. Вто-рой при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке каж-дые две про-ти-во-по-лож-ные сто-ро-ны равны (см. Рис. 7), то этот че-ты-рех-уголь-ник - па-рал-ле-ло-грамм. па-рал-ле-ло-грамм.

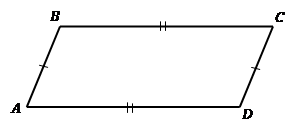
Рис. 7. Вто-рой при-знак па-рал-ле-ло-грам-ма

Тео-ре-ма. Тре-тий при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке диа-го-на-ли точ-кой пе-ре-се-че-ния де-лят-ся по-по-лам (см. Рис. 8), то этот че-ты-рех-уголь-ник - па-рал-ле-ло-грамм. па-рал-ле-ло-грамм.

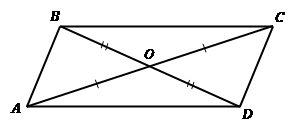
Рис. 8. Тре-тий при-знак па-рал-ле-ло-грам-ма

Те-перь по-вто-рим част-ные слу-чаи па-рал-ле-ло-грам-ма.

3. Определение, свойство и признак прямоугольника

Пря-мо-уголь-ни-ком на-зы-ва-ют па-рал-ле-ло-грамм, у ко-то-ро-го все углы пря-мые (см. Рис. 9).

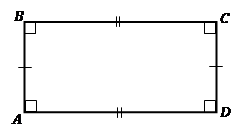
Рис. 9. Пря-мо-уголь-ник

За-ме-ча-ние. Оче-вид-ным эк-ви-ва-лент-ным опре-де-ле-ни-ем пря-мо-уголь-ни-ка (ино-гда его име-ну-ют при-зна-ком пря-мо-уголь-ни-ка) можно на-звать сле-ду-ю-щее. Пря-мо-уголь-ник - это па-рал-ле-ло-грамм с одним углом . Это утвер-жде-ние прак-ти-че-ски оче-вид-но, и мы оста-вим его без до-ка-за-тель-ства, поль-зу-ясь далее как опре-де-ле-ни-ем.

Т.к. пря-мо-уголь-ник, как это видно из опре-де-ле-ния, яв-ля-ет-ся част-ным слу-ча-ем па-рал-ле-ло-грам-ма, то ему при-су-щи все ранее опи-сан-ные свой-ства па-рал-ле-ло-грам-ма, од-на-ко у него име-ют-ся и свои спе-ци-фи-че-ские свой-ства, ко-то-рые мы сей-час рас-смот-рим.

Тео-ре-ма. Свой-ство пря-мо-уголь-ни-ка . Диа-го-на-ли пря-мо-уголь-ни-ка равны (см. Рис. 10).

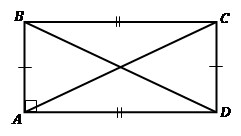
Рис. 10. Свой-ство пря-мо-уголь-ни-ка

Тео-ре-ма. При-знак пря-мо-уголь-ни-ка . Если в па-рал-ле-ло-грам-ме диа-го-на-ли равны, то этот па-рал-ле-ло-грамм - пря-мо-уголь-ник (см. Рис. 11).

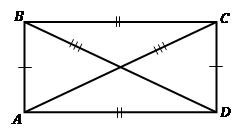
Рис. 11. При-знак пря-мо-уголь-ни-ка

4. Определение и свойство ромба

Ромб - па-рал-ле-ло-грамм, у ко-то-ро-го все сто-ро-ны равны (см. Рис. 12).

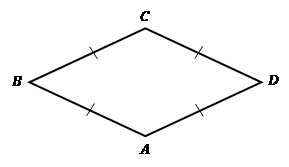
Рис. 12. Ромб

За-ме-ча-ние. Для опре-де-ле-ния ромба до-ста-точ-но ука-зы-вать даже более ко-рот-кое утвер-жде-ние, что это па-рал-ле-ло-грамм, у ко-то-ро-го равны две смеж-ные сто-ро-ны .

Ромб об-ла-да-ет всеми свой-ства-ми па-рал-ле-ло-грам-ма, т.к. яв-ля-ет-ся его част-ным слу-ча-ем, но имеет и свое спе-ци-фи-че-ское свой-ство.

Тео-ре-ма. Свой-ство ромба . Диа-го-на-ли ромба пер-пен-ди-ку-ляр-ны и делят углы ромба по-по-лам (см. Рис. 13).

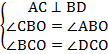
Рис. 13. Свой-ство ромба

5. Определение и свойства квадрата

Квад-рат - 1) пря-мо-уголь-ник, у ко-то-ро-го сто-ро-ны равны; 2) ромб, у ко-то-ро-го углы пря-мые (см. Рис. 14). Ука-зан-ные опре-де-ле-ния эк-ви-ва-лент-ны и при-ме-ня-ют-ся в любой удоб-ной форме.

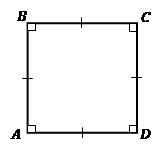
Рис. 14. Квад-рат

Квад-ра-ту при-су-щи свой-ства тех фигур, част-ным слу-ча-ем ко-то-рых он яв-ля-ет-ся (па-рал-ле-ло-грамм, пря-мо-уголь-ник, ромб). Пе-ре-чис-лим их.

Ос-нов-ные свой-ства квад-ра-та (см. Рис. 15):

1. Все углы пря-мые.

2. Диа-го-на-ли равны.

3. Диа-го-на-ли пер-пен-ди-ку-ляр-ны.

4. Точка пе-ре-се-че-ния делит диа-го-на-ли по-по-лам.

5. Диа-го-на-ли делят углы квад-ра-та по-по-лам.

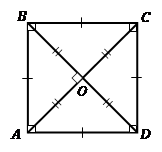
Рис. 15. Свой-ства квад-ра-та

6. Задача на схожесть свойств трапеции и параллелограмма

Те-перь, когда мы пе-ре-чис-ли-ли и вспом-ни-ли ос-нов-ные свой-ства ос-нов-ных изу-чен-ных че-ты-рех-уголь-ни-ков, мы можем за-кре-пить эти зна-ния на при-ме-ре ре-ше-ния задач.

При-мер 1. (Обоб-щен-ная за-да-ча на тра-пе-цию и па-рал-ле-ло-грамм). Дана тра-пе-ция или па-рал-ле-ло-грамм (см. Рис. 16). бис-сек-три-сы углов при бо-ко-вой сто-роне тра-пе-ции (па-рал-ле-ло-грам-ма). Найти угол между бис-сек-три-са-ми .

Ре-ше-ние. Это при-мер за-да-чи, де-мон-стри-ру-ю-щий схо-жесть неко-то-рых свойств па-рал-ле-ло-грам-ма и тра-пе-ции, в нем не важно, какая кон-крет-но из этих двух фигур за-да-на. Изоб-ра-зим ри-су-нок.

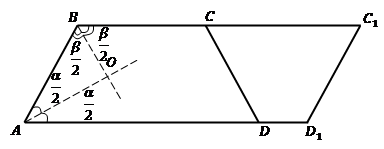
Бис-сек-три-сы, они делят со-от-вет-ству-ю-щие углы по-по-лам, обо-зна-чим их и .

По свой-ству тра-пе-ции (па-рал-ле-ло-грам-ма) .

Рас-смот-рим : .

7. Теорема Фалеса и задача на ее применение

Вспом-ним фор-му-ли-ров-ку тео-ре-мы Фа-ле-са.

Тео-ре-ма Фа-ле-са. Если па-рал-лель-ные пря-мые, ко-то-рые пе-ре-се-ка-ют сто-ро-ны угла, от-се-ка-ют на одной его сто-роне рав-ные от-рез-ки, то они от-се-ка-ют рав-ные от-рез-ки и на дру-гой его сто-роне (см. Рис. 17).

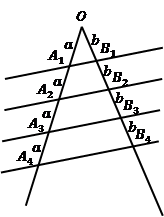
Рис. 17. Тео-ре-ма Фа-ле-са

Рас-смот-рим за-да-чу на тра-пе-цию с при-ме-не-ни-ем тео-ре-мы Фа-ле-са.

При-мер 2. Бо-ко-вая сто-ро-на тра-пе-ции раз-де-ле-на на три рав-ные части, и из точек де-ле-ния про-ве-де-ны к дру-гой сто-роне от-рез-ки, па-рал-лель-ные ос-но-ва-ни-ям. Най-ди-те длину этих от-рез-ков, если ос-но-ва-ния тра-пе-ции равны 2 м и 5 м.

Ре-ше-ние. Изоб-ра-зим Рис. 18 со всеми эле-мен-та-ми, ко-то-рые при-го-дят-ся нам в про-цес-се ре-ше-ния. Из-вест-но, что . Найти длины .

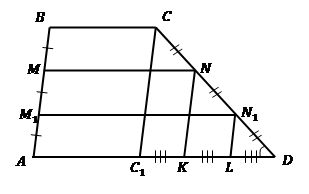
Для того, чтобы вос-поль-зо-вать-ся тео-ре-мой Фа-ле-са от-но-си-тель-но угла , про-ве-дем пря-мые .