История числа пи. История возникновения числа Пи

– отношение длины окружности к ее диаметру, – величина постоянная и не зависит от размеров окружности. Число, выражающее это отношение, принято обозначать греческой буквой 241 (от «perijereia » – окружность, периферия). Это обозначение стало употребительным после работы Леонарда Эйлера, относящейся к 1736, однако впервые оно было употреблено Уильямом Джонсом (1675–1749) в 1706. Как и всякое иррациональное число, оно представляется бесконечной непериодической десятичной дробью:

p = 3,141592653589793238462643… Нужды практических расчетов, относящихся к окружностям и круглым телам, заставили уже в глубокой древности искать для 241 приближений с помощью рациональных чисел. Сведения о том, что окружность ровно втрое длиннее диаметра, находятся в клинописных табличках Древнего Междуречья. Такое же значение числа p есть и в тексте Библии: «И сделал литое из меди море, – от края до края его десять локтей, – совсем круглое, вышиною в пять локтей, и снурок в тридцать локтей обнимал его кругом» (3 Цар. 7. 23). Так же считали и древние китайцы. Но уже во 2 тыс. до н.э. древние египтяне пользовались более точным значением числа 241, которое получается из формулы для площади круга диаметра d :

Этому правилу из 50-й задачи папируса Райнда соответствует значение 4(8/9) 2 » 3,1605. Папирус Райнда, найденный в 1858, назван так по имени его первого владельца, его переписал писец Ахмес около 1650 до н.э., автор же оригинала неизвестен, установлено только, что текст создавался во второй половине 19 в. до н.э. Хотя каким образом египтяне получили саму формулу, из контекста неясно. В так называемом Московском папирусе, который был переписан неким учеником между 1800 и 1600 до н.э. с более древнего текста, примерно 1900 до н.э., есть еще одна интересная задача о вычислении поверхности корзины «с отверстием 4½». Неизвестно, какой формы была корзина, но все исследователи сходятся во мнении, что и здесь для числа p берется то же самое приближенное значение 4(8/9) 2 .

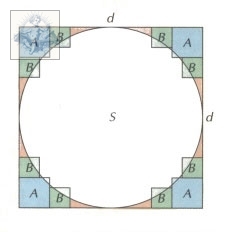
Чтобы понять, каким образом древние ученые получили тот или иной результат, нужно попытаться решить задачу, используя только знания и приемы вычислений того времени. Именно так поступают исследователи старинных текстов, однако решения, которые им удается найти, вовсе не обязательно «те самые». Очень часто для одной задачи предлагается несколько вариантов решения, каждый может выбрать себе по вкусу, однако никто не может утверждать, что именно им пользовались в древности. Относительно площади круга кажется правдоподобной гипотеза А.Е.Раик, автора многочисленных книг по истории математики: площадь круга диаметра d сравнивается с площадью описанного вокруг него квадрата, из которого по очереди удаляются малые квадраты со сторонами и (рис. 1). В наших обозначениях вычисления будут выглядеть так: в первом приближении площадь круга S равна разности между площадью квадрата со стороной d и суммарной площадью четырех малых квадратов А со стороной d :

В пользу этой гипотезы свидетельствуют аналогичные вычисления в одной из задач Московского папируса, где предлагается сосчитать

С 6 в. до н.э. математика стремительно развивалась в Древней Греции. Именно древнегреческие геометры строго доказали, что длина окружности пропорциональна ее диаметру (l = 2 p R ; R – радиус окружности, l – ее длина), а площадь круга равна половине произведения длины окружности и радиуса:

S = ½ l R = p R 2 .

Эти доказательства приписывают Евдоксу Книдскому иАрхимеду.

В 3 в. до н.э. Архимед в сочинении Об измерении круга вычислил периметры вписанных в окружность и описанных около нее правильных многоугольников (рис. 2) – от 6- до 96-угольника. Таким образом он установил, что число p находится между 3 10/71 и 3 1/7, т.е. 3,14084 p p » 3,14166) нашел знаменитый астроном, создатель тригонометрии Клавдий Птолемей (2 в.), но оно не вошло в употребление.

Рис. 2. Архимед в сочинении Об измерении круга вычислил периметры вписанных в окружность и описанных около нее правильных многоугольников – от 6- до 96-угольника. Таким образом он установил, что число p находится между 3 10/71 и 3 1/7, т.е. 3,14084

Индийцы и арабы полагали, что p = . Это значение приводит так же и индийский математик Брахмагупта (598 – ок. 660). В Китае ученые в 3 в. использовали значение 3 7/50, которое хуже приближения Архимеда, но во второй половине 5 в. Цзу Чун Чжи (ок. 430 – ок. 501) получил для p приближение 355/113 (p » 3,1415927). Оно осталось неизвестно европейцам и было вновь найдено нидерландским математиком Адрианом Антонисом только в 1585. Это приближение дает ошибку лишь в седьмом десятичном знаке.

Поиски более точного приближения p продолжались и в дальнейшем. Например, аль-Каши (первая половина 15 в.) в Трактате об окружности (1427) вычислил 17 десятичных знаков p . В Европе такое же значение было найдено в 1597 году. Для этого ему пришлось вычислять сторону правильного 800 335 168-угольника. Нидерландский ученый Лудольф Ван Цейлен (1540–1610) нашел для него 32 правильных десятичных знака (опубликовано посмертно в 1615), это приближение называется лудольфовым числом.

Число p появляется не только при решении геометрических задач. Со времени Ф.Виета (1540–1603) разыскание пределов некоторых арифметических последовательностей, составляемых по простым законам, приводило к тому же числу p . В связи с этим в определении числа p принимали участие почти все известные математики: Ф.Виет, Х.Гюйгенс, Дж.Валлис, Г.В.Лейбниц, Л.Эйлер. Они получали различные выражения для 241 в виде бесконечного произведения, суммы ряда, бесконечной дроби.

Например, в 1593 Ф.Виет (1540–1603) вывел формулу

В 1658 англичанин Уильям Броункер (1620–1684) нашел представление числа p в виде бесконечной непрерывной дроби

,

однако неизвестно, как он пришел к этому результату.

В 1665 Джон Валлис (1616–1703) доказал, что

,

.

Эта формула носит его имя. Для практического нахождения числа 241 она мало пригодна, но полезна в различных теоретических рассуждениях. В историю науки она вошла как один из первых примеров бесконечных произведений.

Готфрид Вильгельм Лейбниц (1646–1716) в 1673 установил следующую формулу:

выражающую число p /4 как сумму ряда. Однако этот ряд сходится очень медленно. Чтобы вычислить p с точностью до десяти знаков, потребовалось бы, как показал Исаак Ньютон, найти сумму 5 млрд чисел и затратить на это около тысячи лет непрерывной работы.

Лондонский математик Джон Мэчин (1680–1751) в 1706, применяя формулу

получил выражение

arctg 1 = 4 arctg – arctg .

Подстановка в него arctg 1 = и рядов для arctg x (arctg x = ) приводит к формуле

которая до сих пор считается одной из лучших для приближенного вычисления p . Чтобы найти те же десять точных десятичных знаков, потребуется всего несколько часов ручного счета. Сам Джон Мэчин вычислил p со 100 верными знаками.

C помощью того же ряда для arctg x и формулы

p = 24 arctg + 8 arctg + 4 arctg

значение числа p было получено на ЭВМ с точностью до ста тысяч десятичных знаков. Такого рода вычисления представляют интерес в связи с понятием случайных и псевдослучайных чисел. Статистическая обработка упорядоченной совокупности указанного количества знаков p показывает, что она обладает многими чертами случайной последовательности.

Есть несколько забавных способов запомнить число p точнее, чем просто 3,14. Например, выучив следующее четверостишие, можно без труда назвать семь десятичных знаков p :

Нужно только постараться

И запомнить все как есть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

(С.Бобров Волшебный двурог )

Подсчет количества букв в каждом слове следующих фраз так же дает значение числа p :

«Что я знаю о кругах?» (p » 3,1416). Эту поговорку предложил Я.И.Перельман.

«Вот и знаю я число, именуемое Пи. – Молодец!» (p » 3,1415927).

«Учи и знай в числе известном за цифрой цифру, как удачу примечать» (p » 3,14159265359).

Учитель одной из московских школ придумал строку: «Это я знаю и помню прекрасно», а его ученица сочинила забавное продолжение: «Пи многие знаки мне лишни, напрасны». Это двустишие позволяет определить 12 цифр.

А так выглядит 101 знак числа p без округления

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679.

В наше время с помощью ЭВМ значение числа p вычислено с миллионами правильных знаков, но такая точность не нужна ни в каких вычислениях. А вот возможность аналитического определения числа p имеет принципиальное значение для геометрии. В частности, в неевклидовой геометрии p также входит в некоторые формулы, но уже не как отношение длины окружности к диаметру (в неевклидовой геометрии это отношение не является постоянным).

В окончательном выяснении арифметической природы числа p решающую роль сыграла замечательная формула Эйлера:

e 2241i = 1,

где e – основание натуральных логарифмов, i = .

Кстати, Эйлеру принадлежат и другие красивые формулы, включающие 241:

,

,

.

В последней формуле в числителе стоят все простые числа, а знаменатели отличаются от них на единицу, причем знаменатель больше числителя, если тот имеет вид 4n + 1, и меньше в противном случае.

Хотя еще с конца 16 в., т.е. с тех пор, как сформировались сами понятия рациональных и иррациональных чисел, многие ученые были убеждены в том, что p – число иррациональное, но только в 1766 немецкий математик Иоганн Генрих Ламберт (1728–1777), основываясь на открытой Эйлером зависимости между показательной и тригонометрической функциями, строго доказал это. Число p не может быть представлено в виде простой дроби, как ни были бы велики числитель и знаменатель.

В 1882 профессор Мюнхенского университета Карл Луиз Фердинанд Линдеман (1852–1939) используя результаты, полученные французским математиком Ш.Эрмитом, доказал, что p – число трансцендентное, т.е. оно не является корнем никакого алгебраического уравнения a n x n + a n– 1 x n– 1 + … + a 1 x + a 0 = 0 с целыми коэффициентами. Это доказательство поставило точку в истории древнейшей математической задачи о квадратуре круга. Тысячелетия эта задача не поддавалась усилиям математиков, выражение «квадратура круга» стало синонимом неразрешимой проблемы. А все дело оказалось в трансцендентной природе числа p .

В память об этом открытии в зале перед математической аудиторией Мюнхенского университета был установлен бюст Линдемана. На постаменте под его именем изображен круг, пересеченный квадратом равной площади, внутри которого начертана буква p .

Библия или книга священного писания ветхого и нового завета , Издание Московской патриархии, 1956
Бородин А.И., Бугай А.С. Биографический словарь деятелей в области математики , Киев, Радянська школа, 1979

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «НОВОАГАНСКАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ CРЕДНЯЯ ШКОЛА №2»

История возникновения

числа Пи.

Выполнила Шевченко Надежда,

ученица 6 «Б» класса

Руководитель: Чекина Ольга Александровна, учитель математики

пгт. Новоаганск

2014

План.

1. Ведение.

Цели.

II. Основная часть.

1)Первый шаг к числу пи.

2)Не разгаданная загадка.

3)Интересные факты.

III. Заключение

Использованная литература.

Введение

Цели моей работы

1)Найти историю происхождения пи.

2)Рассказать интересные факты числа пи

3)Сделать презентацию и оформить доклад.

4) Подготовить выступление на конференцию.

Основная часть.

Пи (π) - буква греческого алфавита, применяемая в математике для обозначения отношения длины окружности к диаметру. Это обозначение происходит от начальной буквы греческих слов περιφέρεια - окружность, периферия и περίμετρος - периметр. Оно стало общепринятым после работы Л. Эйлера, относящейся к 1736г., однако впервые оно было употреблено английским математиком У. Джонсом (1706г.). Как и всякое иррациональное число, π представляется бесконечной непериодической десятичной дробью:

π = 3,141592653589793238462643.

Первый шаг в изучении свойств числа π сделал Архимед. В сочинении «Измерение круга» он вывел знаменитое неравенство: [формула]
Это означает, что π лежит в интервале длиной 1/497. В десятичной системе счисления получаются три правильных значащих цифры: π = 3,14…. Зная периметр правильного шестиугольника и последовательно удваивая число его сторон, Архимед вычислил периметр правильного 96-угольника, откуда и следует неравенство. 96-угольник визуально мало отличается от окружности и является хорошим приближением к ней.
В том же сочинении, последовательно удваивая число сторон квадрата, Архимед нашел формулу площади круга S = π R2. Позднее он дополнил ее также формулами площади сферы S = 4 π R2 и объема шара V = 4/3 π R3.

В древнекитайских трудах попадаются самые разные оценки, из которых самая точная - это известное китайское число 355/113. Цзу Чунчжи (V век) даже считал это значение точным.
Лудольф ван Цейлен (1536-1610) затратил десять лет на вычисление числа π с 20-ю десятичными цифрами (этот результат был опубликован в 1596 году). Применив метод Архимеда, он довёл удвоение до n-угольника, где n=60·229. Изложив свои результаты в сочинении «Об окружности», Лудольф закончил его словами: «У кого есть охота, пусть идёт дальше». После смерти в его рукописях были обнаружены ещё 15 точных цифр числа π. Лудольф завещал, чтобы найденные им знаки были высечены на его надгробном камне. В честь него число π иногда называли «лудольфовым числом».

Но загадка таинственного числа не разрешена вплоть до сегодняшнего дня, хотя по-прежнему волнует ученых. Попытки математиков полностью вычислить всю числовую последовательность часто приводят к курьезным ситуациям. Например, математики братья Чудновские в Политехническом Университете Бруклина специально с этой целью сконструировали суперскоростной компьютер. Однако установить рекорд им не удалось – пока рекорд принадлежит японскому математику Ясумаса Канада, который смог вычислить 1,2 биллиона чисел бесконечной последовательности.

Интересные факты
Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3/14, что соответствует приближённому значению числа Пи.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи», так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.
Мировой рекорд по запоминанию знаков числа π принадлежит японцу Акира Харагути (Akira Haraguchi). Он запомнил число π до 100-тысячного знака после запятой. Ему понадобилось почти 16 часов, чтобы назвать всё число целиком.
Германский король Фридрих Второй был настолько очарован этим числом, что посвятил ему… целый дворец Кастель дель Монте, в пропорциях которого можно вычислить Пи. Сейчас волшебный дворец находится под охраной ЮНЕСКО.

Заключение
В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Всё это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.

Мою работу можно использовать на уроках математики.

Итоги моей работы:

1. Нашла историю происхождения числа пи.
2. Рассказала о интересных фактах числа пи.
3. Узнала много нового о числе пи.
4. Оформила работу и Выступила на конференции.