Образовательный портал. Образование / Среднее образование и школа / Чему равен угол параллелограмма. Повторение: определение и свойства параллелограмма. Определение и основные свойства параллелограмма

Чему равен угол параллелограмма. Повторение: определение и свойства параллелограмма. Определение и основные свойства параллелограмма

08.05.2019

Параллелограмм. Признаки параллелограмма

Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

Теорема.

Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

Существует несколько различных типов четырехугольников. Мы можем понять их, посмотрев на соотношение между сторонами четырехугольника и углами. Параллелограмм - четырехугольник с противоположными сторонами, параллельный и конгруэнтный. Конгруэнт - это слово, которое вы увидите много в геометрии. Конгруэнт означает точно то же самое. В этом случае параллелограмм имеет противоположные стороны, которые параллельны и конгруэнтны, что они имеют одинаковую длину.

Определение и основные свойства параллелограмма

Вот пример параллелограмма. Как насчет углов параллелограмма? Обратите внимание, что противоположные углы в этом параллелограмме одинаковы. На этом рисунке одна пара углов является острой, а одна пара углов тупой. Стрелки указывают на тупые углы. Другие два угла остры. Это иногда верно, но не всегда.

Доказательство.

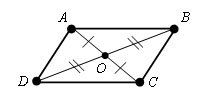
Пусть ABCD – данный параллелограмм, O – точка пересечения диагоналей данного параллелограмма.
Δ AOD = Δ COB по первому признаку равенства треугольников (OD = OB, AO = OC по условию теоремы, ∠ AOD = ∠ COB, как вертикальные углы). Следовательно, ∠ OBC = ∠ ODA. А они являются внутренними накрест лежащими для прямых AD и BC и секущей BD. По признаку параллельности прямых прямые AD и BC параллельны. Так же доказываем, что AB и DC тоже параллельны. По определению данный четырехугольник параллелограмм. Теорема доказана.

Прямоугольник представляет собой параллелограмм с четырьмя прямыми углами. Это означает, что прямоугольник имеет противоположные стороны, параллельные и конгруэнтные, а также четыре прямых. Квадрат представляет собой прямоугольник с четырьмя конгруэнтными сторонами и четырьмя прямыми углами. Обратите внимание, что свойства параллелограмма применимы и к квадратам.

Трапеция - это параллелограмм с одной парой противоположных сторон. Вот пример трапеции. Обратите внимание, что эта трапеция имеет два острых угла и два тупых угла. Обязательно проверьте углы, когда смотрите на трапецию. Это то, что мы называем многоугольником, имеющим четыре стороны. Его параллельные сегменты имеют равные меры и, как и другие четырехугольники, имеют общую сумму внутренних углов, равную 360 °. Параллелограмм имеет две диагонали, которые пересекаются в средней точке, а их противоположные углы имеют равные измерения.

Теорема.

Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.

Пусть ABCD – данный четырехугольник. AD параллельно BC и AD = BC.
Тогда Δ ADB = Δ CBD по первому признаку равенства треугольников (∠ ADB = ∠ CBD, как внутренние накрест лежащие между прямыми AD и BC и секущей DB, AD=BC по условию, DB – общая).
Следовательно, ∠ ABD = ∠ CDB, а эти углы являются внутренними накрест лежащими для прямых AB и CD и секущей DB. По теореме признаке параллельности прямых AB и CD параллельны. Значит, ABCD – параллелограмм. Теорема доказана.

Классификация параллелограммов

Параллельнограммы могут быть некоторых типов: прямоугольника, квадрата и алмаза. Ромб имеет 4 равные стороны и равные противоположные углы, два из которых остры, поэтому они имеют размеры менее 90 °, а два угла тупые, и они представляют измерения более 90 °. Стороны параллельны друг другу; прямоугольник, с другой стороны, имеет четыре равных угла 90 °, а противоположные параллельные стороны равны; простейший квадрат всех, имеет четыре стороны с равными измерениями, а четыре угла равны, каждый из которых равен 90 °.

Теорема.

Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.

Доказательство.

Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA.

Проведем диагональ DB. Сумма углов четырех угольника равна сумме углов треугольников ABD и BCD. Так как сумма углов в треугольнике равна 180 º,
∠ DAB + ∠ BCD + ∠ ABC + ∠ CDA.= 360 º. Так как противолежащие углы в четырехугольнике равны, то ∠ DAB + #8736 ABC = 180 º и ∠ BCD + ∠ CDA = 180 º.
Углы BCD и CDA являются внутренними односторонними для прямых AD и ВС и секущей DC, их сумма равна 180 º, поэтому из следствия к теореме о признаке параллельности прямых, прямые AD и ВС параллельны. Так же доказывается, что AB || DC. Таким образом, четырехугольник ABCD – параллелограмм по определению. Теорема доказана.

Как рассчитать площадь и периметр параллелограмма

Для выполнения вычисления параллелограмма это очень просто. Высота перпендикулярна основанию. Периметр - это не что иное, как сумма всех сторон фигуры.

Отношения между параллелограммами

В этой статье мы можем заключить, что каждый параллелограмм представляет собой квадрат, или алмаз, или прямоугольник, так что все они являются параллелограммами. Следует, однако, отметить, что не каждый параллелограмм представляет собой квадрат, не каждый параллелограмм представляет собой прямоугольник, и не каждый параллелограмм является алмазом, но он, безусловно, будет одним из трех.

При-зна-ки па-рал-ле-ло-грам-ма

1. Определение и основные свойства параллелограмма

Нач-нем с того, что вспом-ним опре-де-ле-ние па-рал-ле-ло-грам-ма.

Опре-де-ле-ние. Па-рал-ле-ло-грамм - че-ты-рех-уголь-ник, у ко-то-ро-го каж-дые две про-ти-во-по-лож-ные сто-ро-ны па-рал-лель-ны (см. Рис. 1).

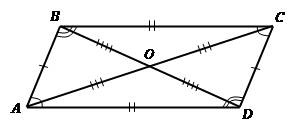
Как рассчитать площадь и периметр параллелограмма

Отношения между параллелограммами

Рис. 1. Па-рал-ле-ло-грамм

Вспом-ним ос-нов-ные свой-ства па-рал-ле-ло-грам-ма :

Для того, чтобы иметь воз-мож-ность поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть уве-рен-ным, что фи-гу-ра, о ко-то-рой идет речь, - па-рал-ле-ло-грамм. Для этого необ-хо-ди-мо знать такие факты, как при-зна-ки па-рал-ле-ло-грам-ма. Пер-вые два из них мы се-год-ня и рас-смот-рим.

2. Первый признак параллелограмма

Тео-ре-ма. Пер-вый при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке две про-ти-во-по-лож-ные сто-ро-ны равны и па-рал-лель-ны, то этот че-ты-рех-уголь-ник - па-рал-ле-ло-грамм . .

Рис. 2. Пер-вый при-знак па-рал-ле-ло-грам-ма

До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 2), она раз-би-ла его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках:

по пер-во-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.

Из ра-вен-ства ука-зан-ных тре-уголь-ни-ков сле-ду-ет, что по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. Имеем, что:

До-ка-за-но.

3. Второй признак параллелограмма

Тео-ре-ма. Вто-рой при-знак па-рал-ле-ло-грам-ма. Если в че-ты-рех-уголь-ни-ке каж-дые две про-ти-во-по-лож-ные сто-ро-ны равны, то этот че-ты-рех-уголь-ник - па-рал-ле-ло-грамм . .

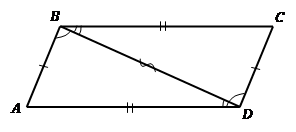
Рис. 3. Вто-рой при-знак па-рал-ле-ло-грам-ма

До-ка-за-тель-ство. Про-ве-дем в че-ты-рех-уголь-ни-ке диа-го-наль (см. Рис. 3), она раз-би-ва-ет его на два тре-уголь-ни-ка. За-пи-шем, что мы знаем об этих тре-уголь-ни-ках, ис-хо-дя из фор-му-ли-ров-ки тео-ре-мы:

по тре-тье-му при-зна-ку ра-вен-ства тре-уголь-ни-ков.

Из ра-вен-ства тре-уголь-ни-ков сле-ду-ет, что и по при-зна-ку па-рал-лель-но-сти пря-мых при пе-ре-се-че-нии их се-ку-щей. По-лу-ча-ем:

па-рал-ле-ло-грамм по опре-де-ле-нию. Что и тре-бо-ва-лось до-ка-зать.

До-ка-за-но.

4. Пример на применение первого признака параллелограмма

Рас-смот-рим при-мер на при-ме-не-ние при-зна-ков па-рал-ле-ло-грам-ма.

При-мер 1. В вы-пук-лом че-ты-рех-уголь-ни-ке Найти: а) углы че-ты-рех-уголь-ни-ка; б) сто-ро-ну .

Ре-ше-ние. Изоб-ра-зим Рис. 4.

па-рал-ле-ло-грамм по пер-во-му при-зна-ку па-рал-ле-ло-грам-ма.

А. по свой-ству па-рал-ле-ло-грам-ма о про-ти-во-по-лож-ных углах, по свой-ству па-рал-ле-ло-грам-ма о сумме углов, при-ле-жа-щих к одной сто-роне.

Б. по свой-ству ра-вен-ства про-ти-во-по-лож-ных сто-рон.

ре-тий при-знак па-рал-ле-ло-грам-ма

5. Повторение: определение и свойства параллелограмма

На-пом-ним, что па-рал-ле-ло-грамм - это че-ты-рёх-уголь-ник, у ко-то-ро-го про-ти-во-по-лож-ные сто-ро-ны по-пар-но па-рал-лель-ны. То есть, если - па-рал-ле-ло-грамм, то (см. Рис. 1).

Па-рал-ле-ло-грамм об-ла-да-ет целым рядом свойств: про-ти-во-по-лож-ные углы равны (), про-ти-во-по-лож-ные сто-ро-ны равны (). Кроме того, диа-го-на-ли па-рал-ле-ло-грам-ма в точке пе-ре-се-че-ния де-лят-ся по-по-лам, сумма углов, при-ле-жа-щих к любой сто-роне па-рал-ле-ло-грам-ма, равна и т.д.

Но для того, чтобы поль-зо-вать-ся всеми этими свой-ства-ми, необ-хо-ди-мо быть аб-со-лют-но уве-рен-ны-ми в том, что рас-смат-ри-ва-е-мый че-ты-рёх-уголь-ник - па-рал-ле-ло-грамм. Для этого и су-ще-ству-ют при-зна-ки па-рал-ле-ло-грам-ма: то есть те факты, из ко-то-рых можно сде-лать од-но-знач-ный вывод, что че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом. На преды-ду-щем уроке мы уже рас-смот-ре-ли два при-зна-ка. Сей-час рас-смот-рим тре-тий.

6. Третий признак параллелограмма и его доказательство

Если в че-ты-рёх-уголь-ни-ке диа-го-на-ли в точке пе-ре-се-че-ния де-лят-ся по-по-лам, то дан-ный че-ты-рёх-уголь-ник яв-ля-ет-ся па-рал-ле-ло-грам-мом.

Дано:

Че-ты-рёх-уголь-ник; ; .

До-ка-зать:

Па-рал-ле-ло-грамм.

Материалы по теме:

Карта сайта