Образовательный портал. Образование / Среднее образование и школа / Деление одного многочлена на другой. Деление многочленов "столбиком" ("уголком")

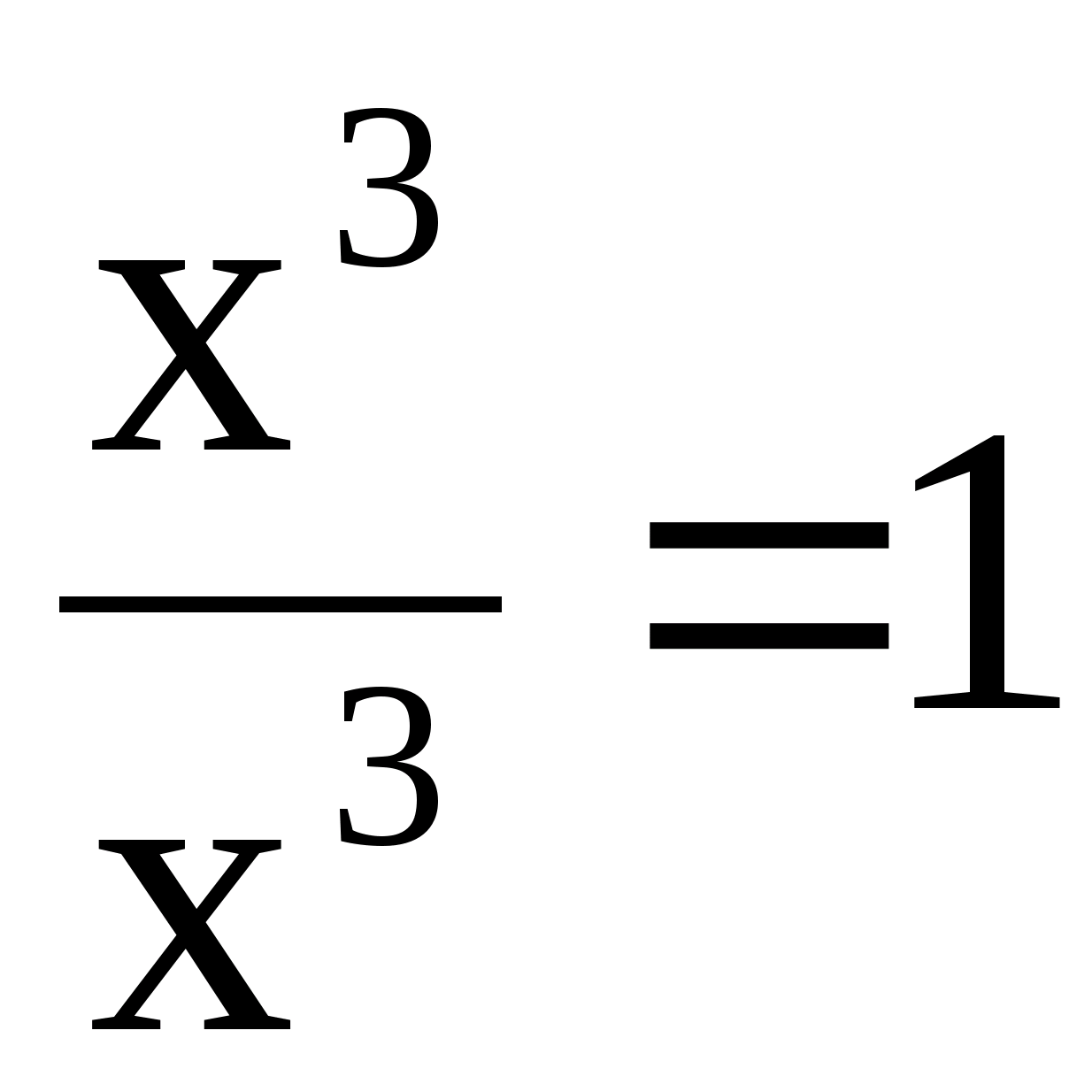
Деление одного многочлена на другой. Деление многочленов "столбиком" ("уголком")

28.08.2019

ДЕЛЕНИЕ МНОГОЧЛЕНОВ. АЛГОРИТМ ЕВКЛИДА

§1. Деление многочленов

При делении многочлены представляются в канонической форме и располагаются по убывающим степеням какой-либо буквы, относительно которой определяется степень делимого и делителя. Степень делимого должна быть больше или равна степени делителя. Результатом деления является единственная пара многочленов – частное и остаток, которые должны удовлетворять равенству: < делимое > = < делитель >  < частное > + < остаток >. Если многочлен степени n P n (x) является делимым, многочлен степени m R k (x)является делителем (n  m), многочлен Q n – m (x) – частное. Степень этого многочлена равна раз-ности степеней делимого и делителя, а многочлен степени k R k (x) является остатком (k < m). То равенство P n (x) = F m (x) Q n – m (x) + R k (x) (1.1) должно выполняться тождественно, то есть, оставаться справедливым при любых действительных значениях х. Ещё раз отметим, что степень остатка k должна быть меньше степени делителя m. Назначение остатка – дополнить произведение многочленов F m (x) и Q n – m (x) до многочлена, равного делимому. Если произведение многочленов F m (x) Q n – m (x) дает многочлен, равный делимому, то остаток R = 0. В этом случае говорят, что деление производится без остатка. Алгоритм деления многочленов рассмотрим на конкретном примере. Пусть требуется разделить многочлен (5х 5 + х 3 + 1) на многочлен (х 3 + 2). 1. Разделим старший член делимого 5х 5 на старший член делителя х 3: . Ниже будет показано, что так находится первый член частного. 2. На очередное (поначалу первое) слагаемое частного умножается делитель и это произведение вычитается из делимого: 5х 5 + х 3 + 1 – 5х 2 (х 3 + 2) = х 3 – 10х 2 + 1. 3. Делимое можно представить в виде 5х 5 + х 3 + 1 = 5х 2 (х 3 + 2) + (х 3 – 10х 2 + 1). (1.2) Если в действии (2) степень разности окажется больше или равна степени делителя (как в рассматриваемом примере), то с этой разностью действия, указанные выше, повторяются. При этом

Результат этого деления переходит в начало линии деления. Вы напишете это в первых двух условиях дивиденда. . Вы вычитаете из дивиденда. Для этого сначала измените знаки продукта умножения. После вычитания он подводит к оставшимся условиям дивиденда. Вычитая это из первых двух членов дивиденда, получим 10х. . Разделите первый член делителя на условный фактор, напишите результат в верхней части линии деления после первого частного, умножьте результат на делитель и затем вычислите, что вычесть из условного частного.

Математика - довольно сложный вопрос, который трудно понять для большинства людей. Особенно, если у маленьких нет прочной основы для понимания более сложных аргументов. Среди различных тем математики, пожалуй, наиболее сложно понять алгебру. Алгебра - одна из самых ненавистных и трудных для обучения для большинства студентов. Продолжая рассуждения, это становится все труднее, поскольку они начинают смешивать все, что может быть сделано, и это может вызвать путаницу, поэтому необходимо знать основы, такие как полиномиальное деление.

Старший член разности х 3 делится на старший член делителя х 3:

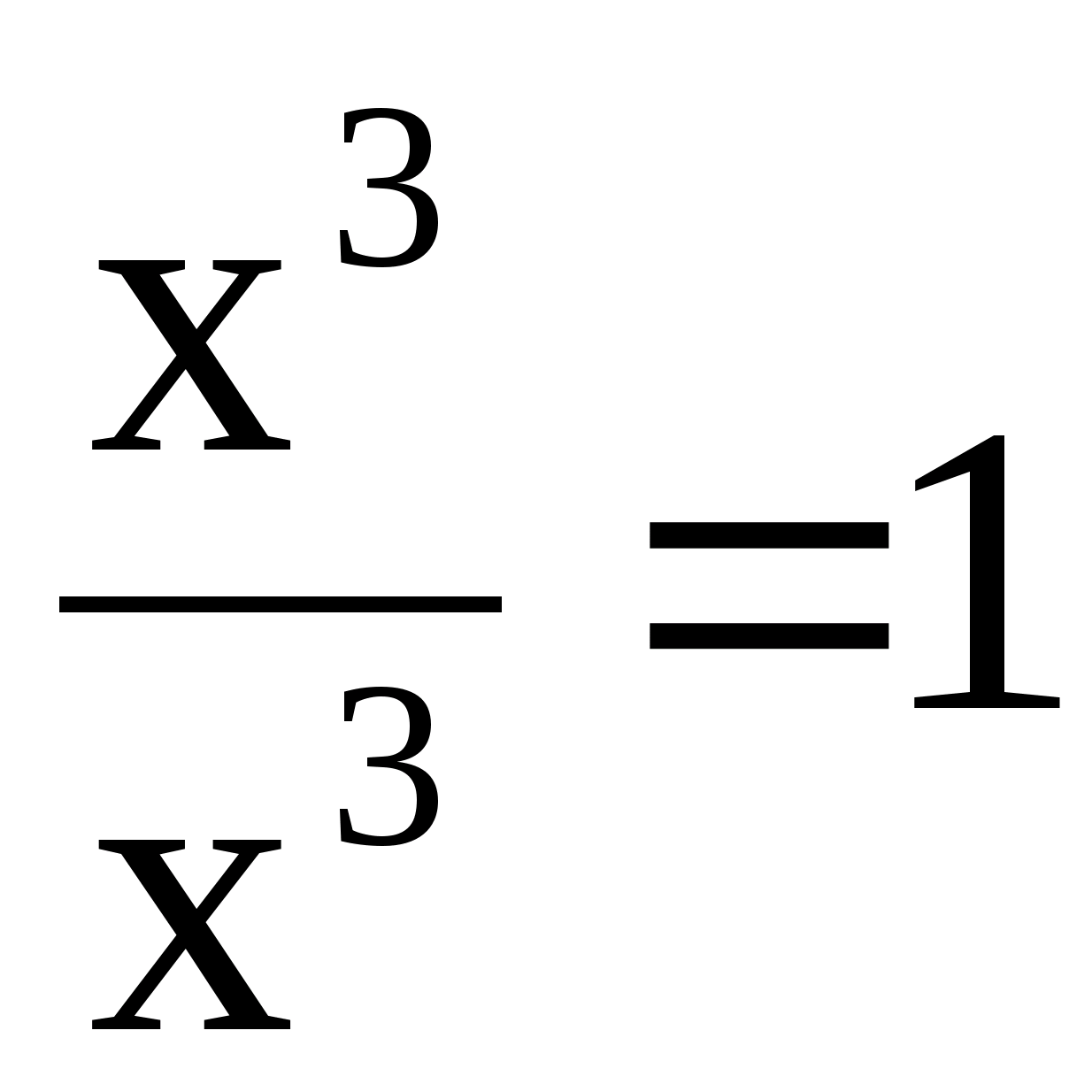. Ниже будет показано, что таким образом находится второе слагаемое в частном. 2. На очередное (теперь уже, второе) слагаемое частного умножается делитель и это произведение вычитается из последней разности х 3 – 10х 2 + 1 – 1(х 3 + 2) = – 10х 2 – 1. 3. Тогда, последнюю разность можно представить в виде х 3 – 10х 2 + 1 = 1(х 3 + 2) + (–10х 2 + 1). (1.3) Если степень очередной разности окажется меньше степени делителя (как при повторе в действии (2)), то деление завершено с остатком, равным последней разности. Для подтверждения того, что частное является суммой (5х 2 + 1), подставим в равенство (1.2) результат преобразования многочлена х 3 – 10х 2 + 1 (см.(1.3)): 5х 5 + х 3 + 1 = 5х 2 (х 3 + 2) + 1(х 3 + 2) + (– 10х 2 – 1). Тогда, после вынесения общего множителя (х 3 + 2) за скобки, получим окончательно 5х 5 + х 3 + 1 = (х 3 + 2)(5х 2 + 1) + (– 10х 2 – 1). Что, в соответствии с равенством (1.1), следует рассматривать как результат деления многочлена (5х 5 + х 3 + 1) на многочлен (х 3 + 2) с частным (5х 2 + 1) и остатком (– 10х 2 – 1). Указанные действия принято оформлять в виде схемы, которая называется «деление уголком». При этом, в записи делимого и последующих разностей желательно производить члены суммы по всем убывающим степеням аргумента без пропуска.

5х 5 + 0х 4 + х 3 + 0х 2 + 0х + 1 х 3 + 2 5х 5 +10х 2 5х 2 + 1

Работа с полиномами - это рутина как для тех, кто недавно начал алгебру, так и для тех, кто так долго мастурбировал. В этом руководстве мы научим вас, как разрешить разделение между двумя полиномами. Это может быть очень полезно во многих областях Математика: от изучения функции при поиске генератора кольцевых многочленов. Посмотрим, как решить полиномиальное деление, предоставив полезные советы, которые помогут вам быстро решить эту операцию.

Во-первых, давайте начнем с определения полинома: полином является просто выражением с константами и переменными, объединенными друг с другом с использованием зависимости, вычитания и умножения. Их роль в математике имеет первостепенное значение. Работа с полиномами довольно проста более сложные, если они переплетаются с различными делениями, которые связаны с различными проблемами.

Х 3 –10х 2 + 0х + 1 х 3 + 2 –10х 2 + 0х – 1 Мы видим, что деление многочленов сводится к последовательному повторению действий:

в начале алгоритма старший член делимого, в последующем, старший член очередной разности делится на старший член делителя; результат деления дает очередное слагаемое в частном, на которое умножается делитель. Полученное произведение записывается под делимым или очередной разностью; из верхнего многочлена вычитается нижний многочлен и, если степень полученной разности больше или равна степени делителя, то с нею повторяются действия 1, 2, 3. Если же степень полученной разности меньше степени делителя, то деление завершено. При этом последняя разность является остатком. Пример №1 6 х 3 + х 2 – 3х – 2 2х 2 – х – 1 6х 3  3х 2  3х 3х + 2

4х 2 + 0х – 2 4х 2  2х  2 2х Таким образом, 6х 3 + х 2 – 3х – 2 = (2х 2 – х – 1)(3х + 2) + 2х. Пример №2

Чтобы упростить разбитый элемент с полиномом числителю и один на знаменатель, необходимо сделать разделение между многочленами. Нарисуйте структуру классического деления и поместите многочлен в левый верхний и многочлен дивизора в верхнем правом углу. В этот момент мы разделим первый член многочлена, который мы делим на первый член многочлена дивизора.

Мы будем иметь новый многочлен, с которым нам придется повторно выполнить операцию. Мы можем сделать это до тех пор, пока Степень полинома для деления будет больше или равна степени полинома дивизора. Как только мы хорошо изучили этот процесс, мы можем применить более сложные полиномиальные операции.

A 5 + b 5 a + b a 5 a 4 b a 4 –a 3 b + a 2 b 2 – ab 3 + b 4 – a 4 b + b 5  a 4 b  a 3 b 2

A 3 b 2 + b 5 a 3 b 2 a 2 b 3 – a 2 b 3 + b 5  a 2 b 3  ab 4 + ab 4 + b 5 – ab 4 b 5 0 Таким образом, a 5 + b 5 = (a + b)(a 4 –a 3 b + a 2 b 2 – ab 3 + b 4). Пример №3

Х 5 – у 5 х – у х 5 х 4 у х 4 + х 3 у + х 2 у 2 + ху 3 + у 4

Х 4 у – у 5 х 4 у  х 3 у 2

Х 3 у 2 – у 5 х 3 у 2  х 2 у 3

Решение разделения между многочленами нелегко в начале, но с небольшим количеством упражнений и следуя инструкциям в этом руководстве, вы можете быстрее решить операции, чтобы понять, как это сделать. Чтобы лучше усвоить концепцию, будет хорошо выполнять множество упражнений, без которых будет трудно продолжить и понять более сложные аргументы. Критерий Эйзенштейна Несводимости.

Для деления полиномов в этих двух классов можно назвать. Эйзенштейна НЕСВОДИМОСТИ критерий. Если полином удовлетворяет критерий Эйзенштейна, можно критиковать его наиболее целочисленная константа, так и в других словах мы можем критиковать максимальный многочлен нулевой степени. Эти 1 и -1. Такой многочлен называется примитивным, и он не может быть обвинен целой константы. Разложимый только тогда, если он является произведением двух многочленов более низких степеней положительного снова с целыми коэффициентами.

Х 2 у 3 – у 5 х 2 у 3  ху 4

Ху 4 – у 5 ху 4 – у 5 0 Таким образом, х 5 – у 5 = (х – у)(х 4 + х 3 у + х 2 у 2 + ху 3 + у 4). Обобщением результатов, полученных в примерах 2 и 3, являются две формулы сокращенного умножения: (х + а)(х 2 n – х 2 n –1 a + х 2 n –2 a 2 – … + a 2n) = х 2n+1 + a 2n + 1 ; (х – a)(х 2n + х 2n–1 a + х 2n–2 a 2 + … + a 2n) = х 2n+1 – a 2n + 1 , где nN . Упражнения Выполнить действия 1. (– 2х 5 + х 4 + 2х 3 – 4х 2 + 2х + 4) : (х 3 + 2). Ответ: – 2х 2 + х +2 – частное, 0 – остаток. 2. (х 4 – 3х 2 + 3х + 2) : (х – 1). Ответ: х 3 + х 2 – 2х + 1– частное, 3 – остаток. 3. (х 2 + х 5 + х 3 + 1) : (1 + х + х 2). Ответ: х 3 – х 2 + х + 1– частное, 2х – остаток. 4. (х 4 + х 2 у 2 + у 4) : (х 2 + ху + у 2). Ответ: х 2 – ху + у 2 – частное, 0 – остаток. 5. (a 3 + b 3 + c 3 – 3abc) : (a + b + c). Ответ: a 2 – (b + c)a + (b 2 – bc + c 2) – частное, 0 – остаток.

Теперь для определения существования или несуществования такого разложения может быть использован критерий Эйзенштейна. В соответствии с критериями и условиями Эйзенштейн, необходимо, что существует простое число р, которое делит и 0 = -49, но квадрат р 2 имеет это число не может быть разделено. Принимая во внимание, что число -49 может быть разделен на несколько ± 1, ± 7 и ± 49, то достаточно, если мы проверить значение 7, которое удовлетворяет условию. условие не верно, так как р = 2 7 2 делит значение = 0 и - выбор числа р = 7 Таким образом, мы не смогли продемонстрировать Неприводимость и никакого другого премьера также не представляется возможным.

§2. Нахождение наибольшего общего делителя двух многочленов

1. Алгоритм Евклида Если каждый из двух многочленов делится без остатка на третий, то этот третий многочлен называется общим делителем первых двух. Наибольшим общим делителем (НОД) двух многочленов называется их общий делитель наибольшей степени. Заметим, что любое число неравное нулю является общим делителем двух любых многочленов. Поэтому, всякое неравное нулю число называется тривиальным общим делителем данных многочленов. Алгоритм Евклида предлагает последовательность действий, которая или приводит к нахождению НОД двух данных многочленов, или показывает, что такой делитель в виде многочлена первой или большей степени не существует. Алгоритм Евклида реализуется в виде последовательности делений. В первом делении многочлен большей степени рассматривается как делимое, а меньшей – как делитель. Если многочлены, для которых находится НОД, имеют одинаковые степени, то делимое и делитель выбираются произвольно. Если при очередном делении многочлен в остатке имеет степень больше или равную 1, то делитель становится делимым, а остаток – делителем. Если при очередном делении многочленов получен остаток, равный нулю, то НОД данных многочленов найден. Им является делитель при последнем делении. Если же при очередном делении многочленов остаток оказывается числом неравным нулю, то для данных многочленов не существует НОД помимо тривиальных. Пример №1 Сократить дробь

. Решение Найдем НОД данных многочленов, применяя алгоритм Евклида 1 ) х 3 + 6х 2 + 11х + 6 х 3 + 7х 2 + 14х + 8 х 3 + 7х 2 + 14х + 8 1 – х 2 – 3х – 2 2

) х 3 + 7х 2 + 14х + 8 – х 2 – 3х – 2 х 3 + 3х 2 + 2х – х – 4

Об этом полиномом по переменной у повторного использования критерия Эйзенштейна и имеет простое число р = 3, находим, что отвечает всем требованиям. Полиномиальной е Поэтому примитивно и поэтому неприводимым. Эйзенштейн критерий Неприводимость может быть естественным образом распространяется на многочлены с рациональными коэффициентами, но большинство из них не хватает. В большинстве случаев, потому что мы хотим знать прямую разложения многочленов, не только показать, что неприводимый многочлен. Этот алгоритм позволяет непосредственно вычислить пару полиномов, коэффициенты полинома указанного.

4х 2 + 12х + 8 4х 2 + 12х + 8 0 Следовательно, многочлен (– х 2 – 3х – 2) является НОД числителя и знамена-теля данной дроби. Результат деления знаменателя на этот многочлен известен. Найдем результат деления числителя. х 3 + 6х 2 + 11х + 6 – х 2 – 3х – 2 х 3 + 3х 2 + 2х – х – 3

3х 2 + 9х + 6 3х 2 + 9х + 6 0 Т

Аким образом, . Ответ:

. 2. Возможности упрощения вычислений НОД в алгоритме Евклида Теорема При умножении делимого на число не равное нулю частное и остаток умножаются на такое же число. Доказательство Пусть P – делимое, F – делитель, Q – частное, R – остаток. Тогда,

Алгоритм Кронекера состоит из четырех этапов. Эта верхняя граница степени полинома г видно из характеристик, связанных с произведением двух многочленов. Не ограничивая общности, можно считать, что Санкт-е ≤, в противном случае мы бы сделали перенумерации. Константа ± 1, но может быть подвергнут критике со всех полиномом, поэтому мы должны попробовать еще трио значений. Поэтому многочлен г е не является фактором. Тем не менее, все еще возможно, что задача будет вычислительной и отнимающей много времени.

Полином называется нулем. Этот номер имеет большое значение для устранения дисбаланса. Теорема о полиномиальном равенстве. Теорема о делении многочленов. Теорема Безу. Теорема о распределении многочленов по факторам. Любой многочлен с вещественными коэффициентами можно разделить на множители не более степени 2 с вещественными координатами.

Умножая данное тождество на число   0, получим

P = F(Q) + R,

Где многочлен P можно рассматривать как делимое, а многочлены Q и R – как частное и остаток, полученные при делении многочлена P на многочлен F. Таким образом, при умножении делимого на число   0, частное и остаток так же умножаются на , ч.т.д Следствие Умножение делителя на число   0 можно рассматривать как умножение делимого на число .

. Следовательно, при умножении делителя на число   0 частное и остаток умножается на . Пример №2 Найти частное Q и остаток R при делении многочленов Решение Для перехода в делимом и делителе к целым коэффициентам умножим делимое на 6, что приведет к умножению на 6 искомого частного Q и остатка R. После чего, умножим делитель на 5, что приведет к умножению частного 6Q и остатка 6R на . В итоге, частное и остаток, полученные при делении многочленов с целыми коэффициентами, в раз будут отличаться от искомых значений частного Q и остатка R, полученных при делении данных многочленов.

Теорема о числе корней многочлена. Мы решаем уравнения многочлена, используя теорему Безу и теорему о касательных элементах многочлена с целыми коэффициентами. Они позволяют разделить полином на множители и, таким образом, читать нули. Легче сделать схему Хорнера.

Очевидно, приведенная выше схема является очевидным предложением при работе с полученными переменными Допустим, есть полиномиальное уравнение. Если это не 0, это означает, что этот многочлен не делится на заданный бином, а число - это остаток от делителя. Как мы вводим числа в таблицу на диаграмме Хорнера? Во-первых, мы добавляем коэффициенты многочлена с последовательными степенями и вводим корень. Тогда коэффициент при наибольшей мощности определяется нижним полем. Мы умножим его на число корней и добавим коэффициент при меньшей мощности и войдем под этим коэффициентом и т.д. если коэффициент при любой заданной мощности равен 0, то мы записываем его в таблицу.

12у 4 – 22ху 3 + 18х 2 у 2 – 11х 3 у + 3х 4 2у 2 – 3ху + 5х 2 12у 4  18ху 3 30х 2 у 2 6у 2 – 2ху – 9х 2 = – 4ху 3 – 12х 2 у 2 – 11х 3 у + 3х 4  4ху 3 6х 2 у 2  10х 3 у – 18х 2 у 2 – х 3 у + 3х 4  18х 2 у 2 27х 3 у  45х 4 – 28х 3 у + 48х 4 =

Следовательно, ; . Ответ:

,

. Заметим, что если наибольший общий делитель данных многочленов найден, то, умножая его на любое число, не равное нулю, мы также получим наибольший делитель этих многочленов. Это обстоятельство дает возможность упрощать вычисления в алгоритме Евклида. А именно, перед очередным делением делимое или делитель можно умножать на числа, подобранные специальным образом так, чтобы коэффициент первого слагаемого в частном был числом целым. Как показано выше, умножение делимого и делителя приведет к соответствующему изменению частного остатка, но такому, что в итоге НОД данных многочленов умножится на некоторое равное нулю число, что допустимо. Пример №3 Сократить дробь

. Решение Применяя алгоритм Евклида, получим 1

Если у нас есть полином в терминах факторов, то существует проблема неравенства. Самый простой способ решить это - построить график функций. Нуль можно прочитать из разложения на факторы. Мы также знаем, что если кратность элемента нечетна, то график меняет знак в этой точке, если кратность четна, многочлен знака не меняется.

Примечание. В следующем примере показан пример. В задаче Задачи было использовано свойство, которое стоит запомнить. При описании свойств многочленов стоит отметить сходство между полиномами и целыми числами. Говорят, что он добавляет, вычитает и умножает как целые числа, так и полиномы. Определения целых делителей, а также полиномиальные делители выглядят одинаково. Вы также можете перейти к полиномам другой концепции - деления с остальными.

) х 4 + 3х 3 + 3х 2 + 3х + 2 х 4 + х 3 – 3х 2 + 4 х 4 х 3  3х 2 4 1 2х 3 + 6х 2 + 3х – 2 2) 2(х 4 + х 3 – 3х 2 + 4) = 2х 4 + 2х 3 – 6х 2 + 8 2х 3 + 6х 2 + 3х – 2 2х 4 6х 3 3х 2  2х х – 2 – 4х 3 – 9х 2 + 2х + 8  4х 3 12х 2  6х4 3х 2 + 8х + 4 3

) 3(2х 3 + 6х 2 + 3х – 2) = 6х 3 + 18х 2 + 9х – 6 3х 2 + 8х + 4 6х 3 16х 2 8х 2х +

2х 2 + х – 6

4

Сформулируем эквивалент этого утверждения для многочленов в поле, обсуждаемом в школе, и дадим ему доказательство. Тогда мы без доказательства докажем общую версию полиномиального эквивалента теоремы деления с остатком. Разделение с остатком целого числа на заданное число и деление многочлена на заданный многочлен состоит в представлении числа или многочлена в форме - форме, описанной в теореме.

Хотя слово «деление» не использует символ разделения в имени для записи этих операций. Прежде чем обсуждать и демонстрировать различные алгоритмы нахождения частного и остального при делении многочлена на биномиал, мы даем важные следствия. Следующая диаграмма Хорнера представляет собой обобщение метода, описанного в решении задач.

) 3х 2 + 8х + 4 х + 2 3х 2 6х 3х + 2

2х + 4 2х + 4 0 Следовательно, многочлен (х + 2) является НОД числителя и знаменателя данной дроби. При этом,

Х 4 + 3х 3 + 3х 2 + 3х + 2 х + 2 х 4 2х 3 х 3 + х 2 + х + 1

Х 3 + 3х 2 + 3х + 2 х 3 2х 2 х 2 + 3х + 2 х 2 2х х + 2 х 2 0 х 4 + х 3 – 3х 2 + 4 х + 2 х 4 +2х 3 х 3 – х 2 – х + 2 – х 3 – 3х 2 + 4  х 3  2х 2 – х 2 + 4  х 2  2х

Начнём с некоторых определений. Многочленом n-й степени (или n-го порядка) будем именовать выражение вида $P_n(x)=\sum\limits_{i=0}^{n}a_{i}x^{n-i}=a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots+a_{n-1}x+a_n$. Например, выражение $4x^{14}+87x^2+4x-11$ есть многочлен, степень которого равна $14$. Его можно обозначить так: $P_{14}(x)=4x^{14}+87x^2+4x-11$.

Схема Хорнера. Система уравнений позволяет рассчитать все коэффициенты \\ и \\, когда коэффициенты равны \\. Биномиальный \\, биномиальный \\. . Схема Хорнера - это быстрый алгоритм вычисления значения полинома для заданного числа. Мы можем использовать его в задачах, подобных задачам. У нас будет двойное преимущество, потому что мы также получим коэффициенты отношения.

В приведенном ниже решении показано, как это можно использовать. Алгоритм, описанный ниже, аналогичен алгоритму записи натуральных чисел. Фактор деления моносилла записывается над линией. Напишите разницу во второй строке. Мы повторяем эту операцию в отношении полученной разности.

Коэффициент $a_0$ называют старшим коэффициентом многочлена $P_n(x)$. Например, для многочлена $4x^{14}+87x^2+4x-11$ старший коэффициент равен $4$ (число перед $x^{14}$). Число $a_n$ называют свободным членом многочлена $P_n(x)$. Например, для $4x^{14}+87x^2+4x-11$ свободный член равен $(-11)$. Теперь обратимся к теореме, на которой, собственно говоря, и будет основано изложение материала на данной странице.

Некоторые люди рекомендуют вместо вычитания большего количества продуктов, чтобы немедленно их сохранить с помощью противоположного знака и добавить его. Эта операция предотвращает ошибки учета. Полученное отношение и остаток совпадают с полученными. Алгоритм, «записанный» с остальной частью многочлена биномиальным, а также сложение, вычитание и умножение полиномов, можно описать без использования переменной \\.

Например, операция разделения из первого примера может быть описана следующим образом. Полная теорема верна. Мы проиллюстрируем этот факт на примере. Как и раньше, каждый раз мы «разделяем» монотон с наивысшей степенью смелой переменной мономенами с наивысшей степенью делительной переменной.

Для любых двух многочленов $P_n(x)$ и $G_m(x)$ можно найти такие многочлены $Q_p(x)$ и $R_k(x)$, что будет выполнено равенство

\begin{equation} P_n(x)=G_m(x)\cdot Q_p(x)+R_k(x) \end{equation}

причём $k < m$.

Словосочетание "разделить многочлен $P_n(x)$ на многочлен $G_m(x)$" означает "представить многочлен $P_n(x)$ в форме (1)". Будем называть многочлен $P_n(x)$ - делимым, многочлен $G_m(x)$ - делителем, многочлен $Q_p(x)$ - частным от деления $P_n(x)$ на $G_m(x)$, а многочлен $R_k(x)$ - остачей от деления $P_n(x)$ на $G_m(x)$. Например, для многочленов $P_6(x)=12x^6+3x^5+16x^4+6x^3+8x^2+2x+1$ и $G_4(x)=3x^4+4x^2+2$ можно получить такое равенство:

Мы проиллюстрируем этот метод на примере. Работа полиномиального распределения по факторам чрезвычайно полезна при решении полиномиальных уравнений и неравенств. Распределение факторов связано с поиском его делителей, т.е. многочленов положительных степеней, через которые многочлен делится. Вы можете использовать сокращенные шаблоны умножения, операции смещения перед круглыми скобками и теорему Бэзута.

Мы проиллюстрируем это в нескольких задачах. В заключение остановимся на основной теореме о распределении многочленов по факторам. Следующий пример показывает, что можно указать многочлен, который не имеет корней и не является квадратной триадой. Этот полином принимает только положительные значения, поэтому корней нет.

$$ 12x^6+3x^5+16x^4+6x^3+8x^2+2x+1=(3x^4+4x^2+2)(4x^2+x)+2x^3+1 $$

Здесь многочлен $P_6(x)$ является делимым, многочлен $G_4(x)$ - делителем, многочлен $Q_2(x)=4x^2+x$ - частным от деления $P_6(x)$ на $G_4(x)$, а многочлен $R_3(x)=2x^3+1$ - остатком от деления $P_6(x)$ на $G_4(x)$. Замечу, что степень остатка (т.е. 3) меньше степени делителя, (т.е. 4), посему условие равенства соблюдено.

Если $R_k(x)\equiv 0$, то говорят, что многочлен $P_n(x)$ делится на многочлен $G_m(x)$ без остатка. Например, многочлен $21x^6+6x^5+105x^2+30x$ делится на многочлен $3x^4+15$ без остатка, так как выполнено равенство:

$$ 21x^6+6x^5+105x^2+30x=(3x^4+15)\cdot(7x^2+2x) $$

Здесь многочлен $P_6(x)=21x^6+6x^5+105x^2+30x$ является делимым; многочлен $G_4(x)=3x^4+15$ - делителем; а многочлен $Q_2(x)=7x^2+2x$ - частным от деления $P_6(x)$ на $G_4(x)$. Остаток равен нулю.

Чтобы разделить многочлен на многочлен часто применяют деление "столбиком" или, как его ещё называют, "уголком". Реализацию этого метода разберём на примерах.

Перед тем, как перейти к примерам, я введу ещё один термин. Он не является общепринятым , и использовать его мы будем исключительно для удобства изложения материала. До конца этой страницы будем называть старшим элементом многочлена $P_n(x)$ выражение $a_{0}x^{n}$. Например, для многочлена $4x^{14}+87x^2+4x-11$ старшим элементом будет $4x^{14}$.

Пример №1

Разделить $10x^5+3x^4-12x^3+25x^2-2x+5$ на $5x^2-x+2$, используя деление "столбиком".

Итак, мы имеем два многочлена, $P_5(x)=10x^5+3x^4-12x^3+25x^2-2x+5$ и $G_2(x)=5x^2-x+2$. Степень первого равна $5$, а степень второго равна $2$. Многочлен $P_5(x)$ - делимое, а многочлен $G_2(x)$ - делитель. Наша задача состоит в нахождении частного и остатка. Поставленную задачу будем решать пошагово. Будем использовать ту же запись, что и для деления чисел:

Первый шаг

Разделим старший элемент многочлена $P_5(x)$ (т.е. $10x^5$) на старший элемент многочлена $Q_2(x)$ (т.е. $5x^2$):

$$ \frac{10x^5}{5x^2}=2x^{5-2}=2x^3. $$

Полученное выражение $2x^3$ - это первый элемент частного:

Умножим многочлен $5x^2-x+2$ на $2x^3$, получив при этом:

$$ 2x^3\cdot (5x^2-x+2)=10x^5-2x^4+4x^3 $$

Запишем полученный результат:

Теперь вычтем из многочлена $10x^5+3x^4-12x^3+25x^2-2x+5$ многочлен $10x^5-2x^4+4x^3$:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5-(10x^5-2x^4+4x^3)=5x^4-16x^3+25x^2-2x+5 $$

На этом первый шаг заканчивается. Тот результат, что мы получили, можно записать в развёрнутой форме:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5=(5x^2-x+2)\cdot 2x^3+5x^4-16x^3+25x^2-2x+5 $$

Так как степень многочлена $5x^4-16x^3+25x^2-2x+5$ (т.е. 4) больше степени многочлена $5x^2-x+2$ (т.е. 2), то процесс деления надобно продолжить. Перейдём ко второму шагу.

Второй шаг

Теперь уже будем работать с многочленами $5x^4-16x^3+25x^2-2x+5$ и $5x^2-x+2$. Точно так же, как и на первом шаге, разделим старший элемент первого многочлена (т.е. $5x^4$) на старший элемент второго многочлена (т.е. $5x^2$):

$$ \frac{5x^4}{5x^2}=x^{4-2}=x^2. $$

Полученное выражение $x^2$ - это второй элемент частного. Прибавим к частному $x^2$

Умножим многочлен $5x^2-x+2$ на $x^2$, получив при этом:

$$ x^2\cdot (5x^2-x+2)=5x^4-x^3+2x^2 $$

Запишем полученный результат:

Теперь вычтем из многочлена $5x^4-16x^3+25x^2-2x+5$ многочлен $5x^4-x^3+2x^2$:

$$ 5x^4-16x^3+25x^2-2x+5-(5x^4-x^3+2x^2)=-15x^3+23x^2-2x+5 $$

Этот многочлен допишем уже под чертой:

На этом второй шаг заканчивается. Полученный результат можно записать в развёрнутой форме:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5=(5x^2-x+2)\cdot (2x^3+x^2)-15x^3+23x^2-2x+5 $$

Так как степень многочлена $-15x^3+23x^2-2x+5$ (т.е. 3) больше степени многочлена $5x^2-x+2$ (т.е. 2), то продолжаем процесс деления. Перейдём к третьему шагу.

Третий шаг

Теперь уже будем работать с многочленами $-15x^3+23x^2-2x+5$ и $5x^2-x+2$. Точно так же, как и на предыдущих шагах, разделим старший элемент первого многочлена (т.е. $-15x^3$) на старший элемент второго многочлена (т.е. $5x^2$):

$$ \frac{-15x^3}{5x^2}=-3x^{2-1}=-3x^1=-3x. $$

Полученное выражение $(-3x)$ - это третий элемент частного. Допишем к частному $-3x$

Умножим многочлен $5x^2-x+2$ на $(-3x)$, получив при этом:

$$ -3x\cdot (5x^2-x+2)=-15x^3+3x^2-6x $$

Запишем полученный результат:

Теперь вычтем из многочлена $-15x^3+23x^2-2x+5$ многочлен $-15x^3+3x^2-6x$:

$$ -15x^3+23x^2-2x+5-(-15x^3+3x^2-6x)=20x^2+4x+5 $$

Этот многочлен допишем уже под чертой:

На этом третий шаг заканчивается. Полученный результат можно записать в развёрнутой форме:

$$ 10x^5+3x^4-12x^3+25x^2-2x+5=(5x^2-x+2)\cdot (2x^3+x^2-3x)+20x^2+4x+5 $$

Так как степень многочлена $20x^2+4x+5$ (т.е. 2) равна степени многочлена $5x^2-x+2$ (т.е. 2), то продолжаем процесс деления. Перейдём к четвёртому шагу.

Четвёртый шаг

Теперь уже будем работать с многочленами $20x^2+4x+5$ и $5x^2-x+2$. Точно так же, как и на предыдущих шагах, разделим старший элемент первого многочлена (т.е. $20x^2$) на старший элемент второго многочлена (т.е. $5x^2$):

$$ \frac{20x^2}{5x^2}=4x^{2-2}=4x^0=4. $$

Полученное число $4$ - это четвёртый элемент частного. Допишем к частному $4$