Определение двугранного и многогранного угла. Трехгранный угол определение. I. Организационный момент
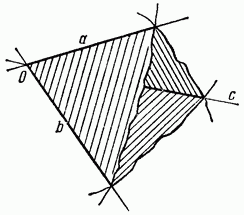
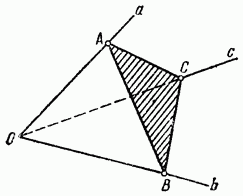
Фигура, образованная тремя лучами, исходящими из одной точки О и не лежащими в одной плоскости, и тремя частями плоскостей, заключенных между этими лучами, называется трехгранным углом (рис. 352).
Точка О называется вершиной угла, лучи а, b, с - его ребрами, части плоскостей . Грани суть плоские углы, называемые также плоскими углами данного трехгранного угла. Углы между плоскими гранями называются двугранными углами данного трехгранного угла.
Твердая геометрия всегда очаровывала меня и вдохновила мою воображаемую силу. В университетские дни у него была привычка читать вслух и объяснять себе часть учебного процесса. В плоскости, если две прямые линии нарисованы, они пересекают друг друга в какой-то точке. Но когда они параллельны друг другу, они сохраняют постоянное расстояние между собой по всей своей бесконечной длине в обоих направлениях. Следовательно, они никогда не пересекаются друг с другом. Две непараллельные прямые в плоскости, пересекающиеся друг с другом, имеют вращательное расстояние между ними.
Теорема 1. В трехгранном угле каждый плоский угол меньше суммы двух других.
Доказательство. Достаточно доказать теорему для наибольшего из плоских углов. Пусть наибольший плоский угол трехгранного угла на рис. 353. Построим в плоскости угол , равный углу его сторона b пройдет внутри угла угол наибольший из плоских углов!).

II. Устная работа
Когда одна из прямых вращается вокруг точки пересечения, она будет совпадать с другой прямой после некоторого вращения. Это вращательное расстояние между прямыми линиями называется угловым. Одно полное вращение делится на 360 частей с целью количественного определения количества вращения, каждая часть которого называется степенью. Когда две прямые в плоскости пересекаются друг с другом, они фактически создают четыре угла с противоположными углами равных величин.
Легко видеть, что смежные углы составляют 180 градусов или половину вращения. Эти четыре угла на самом деле являются четырьмя внутренними углами параллелограмма! Мы также можем легко видеть, что две пересекающиеся прямые в плоскости делят плоскость на четыре квадранта. Если прямые линии перпендикулярны друг другу, они делят плоскость на четыре равных квадранта. Теперь перейдем к третьему измерению. Рассмотрим две плоскости, параллельные друг другу. Они поддерживают постоянное расстояние между ними по всей их бесконечной поверхности.
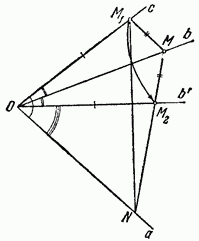
Отложим на прямых с и b какие-либо равные отрезки Проведем через точки произвольную плоскость, пересекающую лучи а и b в точках N и М соответственно.
Треугольники равны, как имеющие равные углы, заключенные между равными сторонами. Покажем, что угол с вершиной О в больше угла с той же вершиной в . Действительно, эти углы заключены между парами равных сторон, третья же сторона больше в треугольнике
Они никогда не пересекаются. Но две непараллельные плоскости пересекаются друг с другом, в некотором месте, по прямой. У них есть вращательное расстояние между ними. Это похоже на плоский угол, и это вращательное расстояние известно как двугранный угол, так как угол между двумя плоскостями изменяется от 0 до 360 градусов. Рассмотрим теперь третью плоскость, не параллельную ни одной из двух предыдущих плоскостей. Пусть эта плоскость пересекает каждую из двух предыдущих плоскостей вдоль двух разных и непараллельных прямых.
Все эти три самолета будут встречаться в общей точке. На этом этапе образуется телесный угол, известный как. В общем случае угол представляет собой вращательное расстояние. Аналогично, трехгранный угол также является мерой суммы вращательных расстояний в двух направлениях, т.е. вращения вокруг двух краев трехгранных пересечений. Поэтому некоторое время его называют квадратным или квадратным градусом. Трехгранные углы меняются от 0 до 720 кв. Поскольку радиус вращает полный раунд в, скажем, в вертикальной плоскости, мы получаем вертикальный круг.
Отсюда видно, что сумма двух плоских углов больше третьего плоского угла что и требовалось доказать.
Теорема 2. Сумма плоских углов трехгранного угла меньше четыре прямых.
Доказательство. Возьмем три точки А, В и С на ребрах трехгранного угла и проведем через них секущую плоскость, как показано на рис. 354. Сумма углов треугольника ABC равна Следовательно, сумма шести углов ОАС, ОАВ, ОСА, ОСВ, ОВС, ОВА больше, чем как по предыдуще теореме . Но сумма углов трех треугольников ОАВ, ОВС, ОСА в гранях трехгранного угла равна . Таким образом, на долю плоских углов трехгранного угла остается меньше четырех прямых: . Эта сумма может быть сколь угодно малой («трехгранный шпиль») или сколь угодно близкой к если уменьшать высоту пирамиды SABC на рис. 355, сохраняя ее основание, то сумма плоских углов при вершине S будет стремиться к
Теперь рассмотрим телесный угол, образованный частичным сферическим сегментом в центре. Он задается как площадь поверхности сегмента, деленная на квадрат радиуса. Когда три плоскости пересекают друг друга в пространстве, они фактически создают восемь трехгранных углов.
IV. Закрепление изученного материала
Эти восемь трехгранных углов фактически представляют собой восемь твердых углов параллелепипеда! Мы также видим, что три пересекающиеся плоскости делят 3-мерное пространство на восемь октантов. Если эти три плоскости перпендикулярны друг другу, они делят 3-мерное пространство на восемь равных октантов. Другие углы трехгранного угла.
Сумма двугранных углов трехгранного угла также имеет границы. Ясно, что каждый из двугранных углов и потому сумма их менее . Для той же пирамиды на рис. 355 эта сумма по мере уменьшения высоты пирамиды приближается к своей границе Можно также показать, что сумма эта всегда хотя может отличаться от сколь угодно мало.
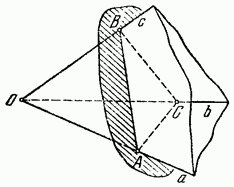
Хотя мы говорим о трех плоскостях, составляющих трехгранный угол, нам удобно говорить о трехгранном угле, образованном тремя прямыми линиями, встречающимися в точке. Поэтому мы говорим о вершинном угле в виде плоского угла между любыми двумя ребрами в вершине трехгранного угла. Двугранными углами являются углы между смежными плоскостями, составляющие любые трехгранные или многогранные углы. Телесный угол, двугранный угол и угол вершины обычно обозначаются как Ω, Φ и θ. Интересно видеть ниже, как эти углы связаны друг с другом, скажем, для случая.
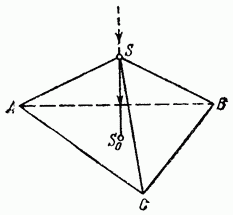
Таким образом, для плоских и двугранных углов трехгранного угла имеют место неравенства
![]()
Имеется существенное сходство между геометрией треугольника на плоскости и геометрией трехгранного угла. При этом можно проводить аналогию между углами треугольника и двугранными углами трехгранного угла, с одной стороны, и между сторонами треугольника и плоскими углами трехгранного угла - с другой. Например, при указанной замене понятий сохраняют силу теоремы о равенстве треугольников. Приведем соответствующие формулировки параллельно:
Точка, общая для всех плоскостей, ограничивающих угол многогранника, называется вершиной. Пересечения каждой из двух последовательных параллельных плоскостей называются ребрами. Углы, образованные каждым из двух последовательных ребер, называются гранями, а диэдры, образованные каждой из двух последовательных граней, называются диэдрами угла многогранника.
Каждая точка биссектрисовой плоскости находится на равном расстоянии от граней упомянутого двугранного угла. Биссекторная плоскость двугранного угла. Площадь ортогональной проекции плоской области на данной плоскости, равна площади области с косинус двугранного угла, определяемого плоскостью области и заданной плоскости.

Однако два трехгранных угла, у которых равны соответственные двугранные углы, равны между собой. Между тем два треугольника, углы которых соответственно равны, подобны, но не обязательно равны. Для трехгранных углов, как и для треугольников, ставится задача решения трехгранного угла, т. е. задача отыскания одних его элементов по другим заданным. Приведем пример подобной задачи.
Пространство вокруг этой точки и между стенами и крышей называется трехгранной. В общем случае угол многогранника вызывается в область пространства, ограниченного тремя или более плоскостями, которые разрезаются по два в два по совпадающим линиям в одной и той же вершине. Как и в двугранном, у углов многогранника есть грань и края: Идентифицируйте их в прилагаемом рисунке. По мере увеличение числа диэдра, многогранник называется: трехгранник, тетраэдр, пятигранник, шестигранник и т.д. может быть каждый из двух типов: выпуклый или вогнутыми, в соответствии с разделом, полученным при разрезании плоскости представляет собой выпуклый многоугольник или вогнутой, соответственно.
Задача. Даны плоские углы трехгранного угла. Найти его двугранные углы.
Решение. Отложим на ребре а отрезок и проведем нормальное сечение ABC двугранного угла а. Из прямоугольного треугольника ОАВ находим Также имеем
Для ВС находим по теореме косинусов примененной к треугольнику ВАС (для краткости плоские углы обозначаем просто ab, ас, bс, двугранные - а, b, с)
Теорема: когда два триэдра являются дополнительными или полярными, верно, что грани одного из них являются дополнениями диэдров другого триэдра и взаимно. Вычислите количество ребер. Вычислить меру наибольшего двугранного угла двугранного угла, в котором две его грани измеряют 53, а третий.
I. Организационный момент
Тогда измерение одного из его двугранных углов. Существует выпуклый многогранник, ограниченный определенным числом треугольных и четырехугольных областей, а также тремя гексагональными областями. Количество граней плюс число вершин плюс число ребер многогранника. Рассчитайте, сколько граней знает, что сумма мер углов их граней равна.
Теперь применим теорему косинусов к треугольнику ВОС:
Отсюда находим
и аналогично
По этим формулам можно найти двугранные углы, зная плоские углы. Отметим еще без доказательства замечательное соотношение
![]()
называемое теоремой синусов.
Объяснение глубокой аналогии между геометрией трехгранного угла и геометрией треугольника нетрудно получить, если провести следующее построение. Поместим в вершину трехгранного угла О центр сферы единичного радиуса (рис. 357).
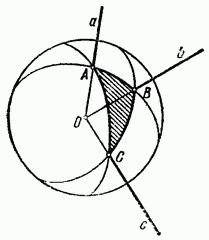
Тогда ребра пересекут поверхность сферы втрехточках А, В, С, грани угла высекут на сфере дуги больших кругов АС, АВ, ВС. На сфере образуется фигура ABC, называемая сферическим треугольником. Дуги («стороны» треугольника) измеряются плоскими углами трехгранного угла, углы при вершинах суть плоские углы двугранных углов. Поэтому решение трехгранных углов есть не что иное, как решение сферических треугольников, которое составляет предмет сферической тригонометрии. Соотношения (243.1) и (243.2) относятся к числу основных соотношений сферической тригонометрии. Сферическая тригонометрия имеет важное значение для астрономии. Таким образом, теория трехгранных углов есть теория сферических треугольников и потому во многом сходна с теорией треугольника на плоскости. Различие этих теорий состоит в том, что: 1) у сферического треугольника и углы и стороны измеряются в угловой мере, поэтому, напрнмер, в теореме синусов фигурируют не стороны, а синусы сторон АВ, АС, ВС;
Методическая разработка урока математики в 11 классе
учителя математики высшей квалификационной категории
Пономаренко Галины Ивановны
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа с. Осиновка»
Михайловского муниципального района Приморского края
Урок геометрии. 11 класс.
 учитель математики высшей
учитель математики высшей
квалификационной категории
e -mail : galina _ p 70@ mail . ru
2015 г.
Тема: « Двугранный угол. Трёхгранный и многогранный углы ». 11 класс.
Тип урока: изучение нового материала
Цели урока:
повторить определение угла на плоскости, угла между прямыми, угла между прямой и плоскостью;
ввести определение двугранного угла, понятие его граней и ребра;
ввести понятие линейного угла двугранного угла;
ввести понятие трехгранного и многогранного углов;
рассмотреть задачи на применение этих понятий.
Структура урока:
I этап Организационный
II этап Устная работа (актуализация знаний)
III этап Изучение нового материала
IV этап Закрепление изученного материала
V этап Итог урока. Постановка домашнего задания
Ход урока
(СЛАЙД № 1) Сообщение темы, цели урока.
II . Устная работа
Повторить материал за курс 10 класса, используя слайды презентации по следующим темам:
1. Взаимное расположение прямых в пространстве (СЛАЙД № 2)
2. Дайте определение угла. Какие бывают углы?
3. Дайте определение угла между прямыми.
4. Взаимное расположение прямой и плоскости (СЛАЙД № 3)
5. Дайте определение угла между прямой и плоскостью.
6. Взаимное расположение двух плоскостей (СЛАЙД № 4)
7. Дайте определение параллельных плоскостей.
8. Дайте определение перпендикулярных плоскостей.
III . Изучение нового материала.
1. (СЛАЙД № 5)
Преподаватель дает определение двугранного угла. Поясняет, что называется его гранями и ребрами.
2. (СЛАЙД № 6)
Преподаватель дает определение линейного угла двугранного угла.
3. (СЛАЙД № 7)
Преподаватель, используя готовые чертежи, доказывает, что все линейные углы двугранного угла равны друг другу.
4. (СЛАЙД № 8)
Величина двугранного угла.
5. (СЛАЙД № 9)
Алгоритм построения двугранного угла:
1. На ребре угла выбрать точку
2. Провести в гранях через неё полупрямые, перпендикулярные ребру.
(Основание: признак перпендикулярности прямой и плоскости )
6. (СЛАЙД № 10)
Преподаватель дает понятие трёхгранного и многогранного углов, понятие их граней и ребер согласно материалу учебника: Погорелов А.В . «Геометрия. 10-11 классы: учебник для общеобразовательных учреждений: базовый и проф. уровни»
IV . Закрепление изученного материала
1. (СЛАЙД № 11)
Найти двугранный угол между: а) плоскостями ABB 1 A 1 и BB 1 C 1 C
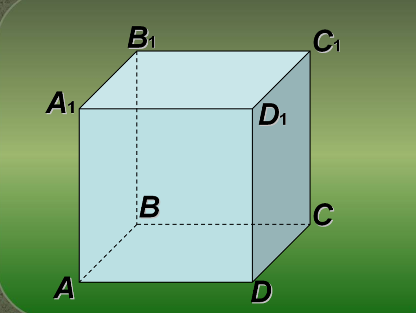
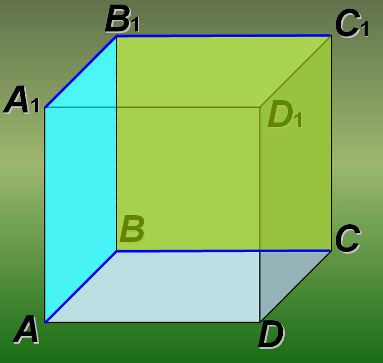
Примечание:
Далее, после ответа учащихся, учитель наводит курсор на буква A 1 (курсор примет вид руки), если учащийся назвал A 1 B 1 C 1 или на букву A , если был назван A BC и делает щелчок мышью, чтобы выделить угол цветом.
Найти двугранный угол между: б) плоскостью AA
1 B
1 B
и плоскостью диагонального
сечения BB
1 D
1 D
П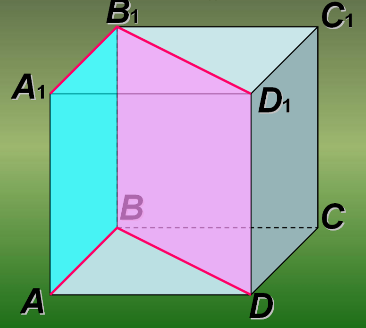 римечание:
римечание:
По щелчку мыши грани окрашиваются в другие цвета.
Далее, после ответа учащихся, учитель наводит курсор на буква, если учащийся назвал A 1 B 1 D 1 или на букву D , если был назван A B D и делает щелчок мышью, чтобы выделить угол цветом
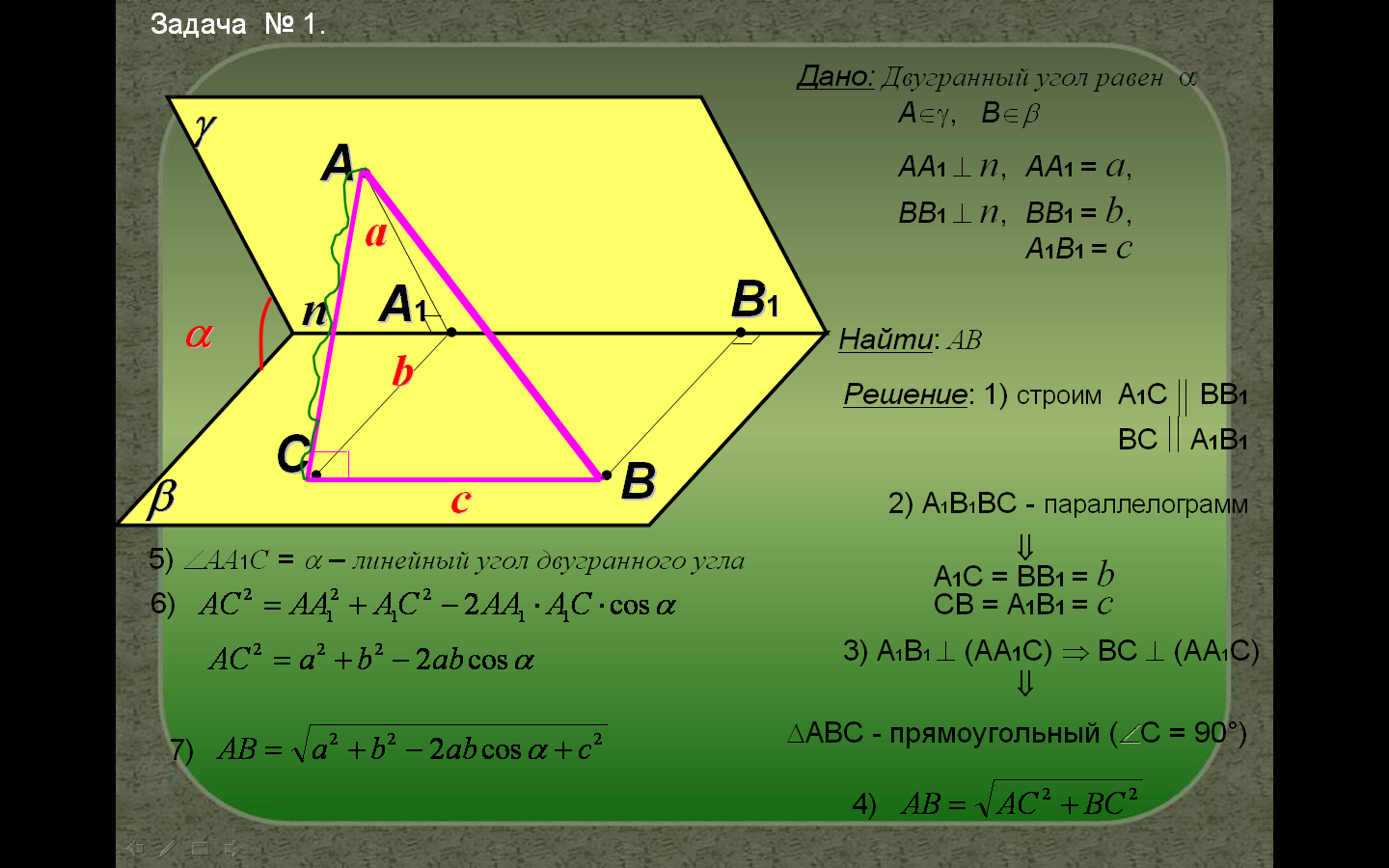
2. Задача № 1 (разобрана в учебнике)(СЛАЙД № 11)
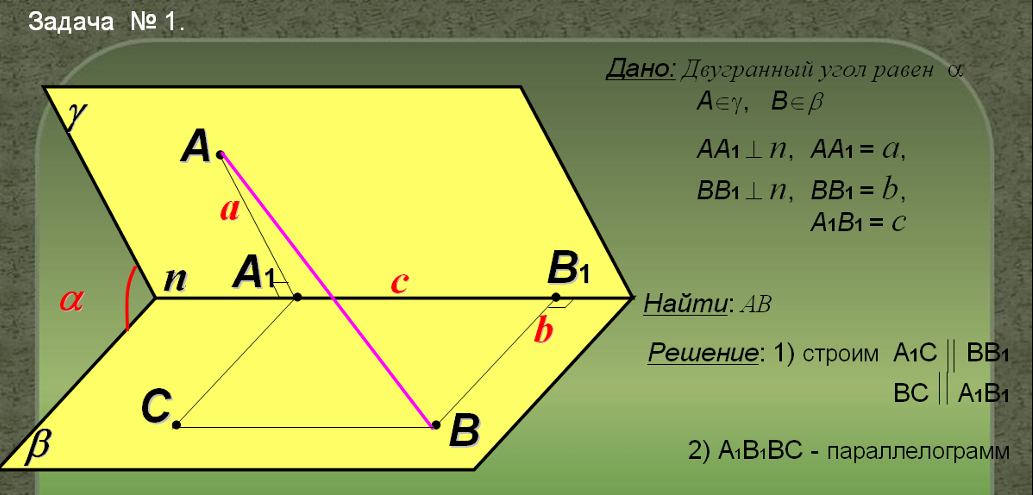
Вопросы для повторения:
1. Определение параллелограмма
2. Свойство параллелограмма
3. Признаки перпендикулярности прямой и плоскости
4. Свойство параллельных прямых, одна из которых перпендикулярна плоскости .
5. Определение перпендикулярных прямой и плоскости.
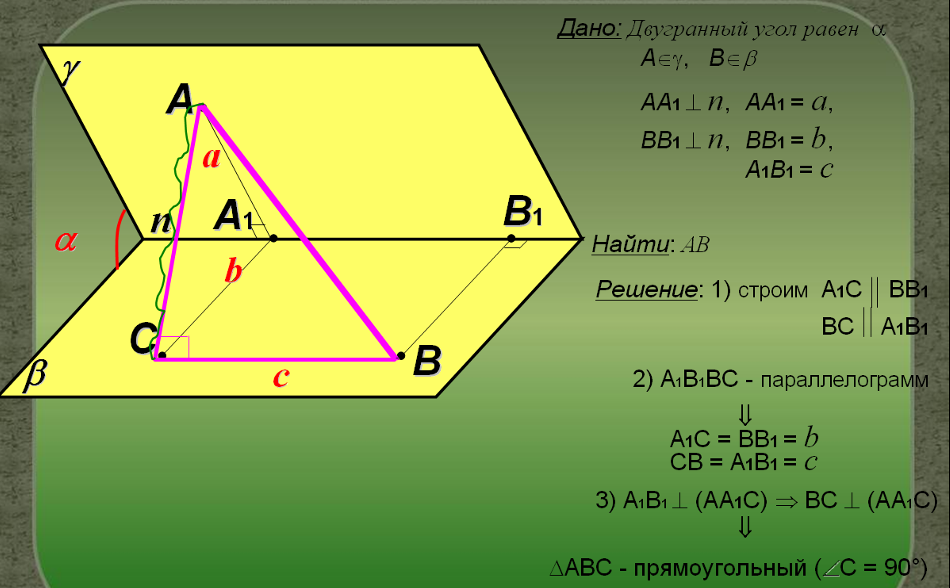
Вопросы: 1. Определение величины двугранного угла.
2. Теорема косинусов.
3.Теорема Пифагора
V . Итог урока. Постановка домашнего задания
1. Что такое двугранный угол (грань угла, ребро угла)?
2. Что такое линейный угол двугранного угла?
3. Почему мера двугранного угла не зависит от выбора линейного угла?
4. Что такое трехгранный угол (грань угла, ребро угла)?
5. Объясните, что такое плоские и двугранные углы трёхгранного угла.
(СЛАЙД № 5) Домашнее задание:
п. 39, 40
вопрос 1-5 на стр. 81
№ 1(2), № 2 на стр. 83
Использованная литература:
1.
Погорелов А.В.
Геометрия. 10-11 классы: учебник для общеобразовательных
учреждений: базовый и профильный уровни
–М.: Просвещение, 2014
2.
Геометрия. 11 класс: Поурочные планы по учебнику Погорелова А.В.
/
Состав. Гилярова М.Г.
-
Волгоград: ИТД «Корифей», 2008
3.
Геометрия. 11 класс: поурочные планы по учебнику А.В. Погорелова. -Ч.I
/
Авт.-составЮ.А. Киселева.
-
Волгоград: Учитель, 2008. – 211 с.
- Какие меры относились к политике военного коммунизма
- Лунин, михаил сергеевич Лунин Николай Иванович: витамины
- Скончался академик борис сергеевич соколов Соколов, Борис Сергеевич Информацию О
- Рецепты варенья из кабачков с лимоном, с курагой и в ананасовом соке
- Как приготовить вкусные куриные сердечки с картофелем в мультиварке Куриные сердечки рецепт в мультиварке с картофелем
- Сырный суп с курицей и грибами Куриный суп с сыром и грибами
- Четверка монет таро значение

 Live Journal
Live Journal Facebook
Facebook Twitter
Twitter