Четырехугольник стороны равны вычислим. Четырехугольники, вписанные в окружность. Частные случаи четырехугольников
1. Определение четырехугольника.
Четырехугольник - это геометрическая фигура, образованная из четырех точек (никакие три из которых не лежат на одной прямой) и четырех отрезков, последовательно соединяющих эти точки.
2. Теорема о сумме углов четырехугольника.
Сумма углов четырехугольника равна 360 градусов.
Параллелограммы можно разделить на три группы. Следствием этого определения является то, что диагонали алмазов перпендикулярны; Прямоугольники: параллелограммы с четырьмя внутренними углами, равными 90 °. Следствием этого определения является то, что диагонали прямоугольника конгруэнтны; Квадраты: параллелограммы, которые представляют собой прямоугольники и лепешки, т.е. квадраты имеют четыре угла 90 °, а их четыре стороны равны. Следствием этого определения является следующее: диагонали квадрата перпендикулярны и конгруэнтны. Трапеции - это то, что у них есть только пара параллельных противоположных сторон.
3. Определение выпуклого четырехугольника.
Выпуклый четырехугольник - это такой четырехугольник, все вершины которого лежат по одну сторону от прямой, содержащей любую его сторону.
4. Свойство диагоналей выпуклого четырехугольника.
Диагонали выпуклого четырехугольника пересекаются.
5. Свойства диагоналей невыпуклого четырехугольника.
Какие виды четырехугольников изучаются в школьной программе
Таким образом, другая пара сторон не может быть параллельной, потому что трапеция станет параллелограммом. Параллельные стороны трапеции называются основаниями. Более крупный обычно называют более крупной базой, а другой называется меньшей базой. Расстояние между этими двумя основаниями - это высота трапеции.
Соответствует сумме четырех сторон этой плоской фигуры. Помните, что квадрат представляет собой правильный четырехугольник, который имеет стороны с теми же измерениями. Таким образом, эта цифра состоит из четырех прямых углов. Периметр квадрата вычисляется по формуле.
Диагонали невыпуклого четырехугольника не пересекаются.
6. Дельтоид.
Дельтоид это четырехугольник, у которого две соседние стороны равны между собой, а две другие равны между собой.
7. Свойство диагоналей дельтоида.
Диагонали дельтоида лежат на взаимноперпендикулярных прямых.
8. Параллелограмм.
Узнайте, как рассчитать периметры других плоских фигур. В отличие от периметра, площадь - это измерение поверхности фигуры. Таким образом, площадь квадрата вычисляется по формуле. Как насчет узнать об этом больше? Единица измерения площади всегда будет дана в см 2 или м 2. Это потому, что умножая на сантиметр на сантиметр или метр на метр, у нас есть квадрат меры.
Обратите внимание, что по периметру единица измерения составляет сантиметр или метр, так как выполняется сумма, а не умножение. Проходя по линии между одним концом и другим квадратом, он образует два прямоугольных треугольника, имеющих угол 90 °. Эта линия, которая разрезает фигуру на две половины, называется диагональю.
Параллелограмм это четырехугольник, противоположные стороны которого попарно параллельны.
9. Диагональ параллелограмма.
Диагональ параллелограмма это отрезок, соединяющий противоположные его вершины.
10. Высота параллелограмма.
Высота параллелограмма это расстояние между параллельными его сторонами.
Когда квадрат появляется внутри круга, он называется «квадратным вписанным». Этот тип фигуры очень часто встречается в тестах, вестибюлях и конкурсах. Для вычисления измерений этого рисунка достаточно использовать теорему Пифагора. Вычислите периметр квадратов.
Сначала давайте использовать формулу области, чтобы узнать значение сторон этого квадрата. Если сторона этого квадрата измеряет 30 см, чтобы найти периметр, просто добавьте это значение четыре раза. Здесь мы проведем исследование, чтобы выяснить сумму углов всех четырехугольников.
11. Основные свойства параллелограмма.
- Противоположные углы попарно равны
- Сумма соседних углов равна 180 градусов
- Диагональ делит параллелограмм на два равных треугольника
- Диагонали пересекаются и делятся точкой пересечения пополам
Противоположные стороны попарно равны
12. Дополнительные свойства параллелограмма.
Один из самых известных четырехугольников - это прямоугольник. Да, это то, что вы подумали, тот, который имеет все правильные углы. Добавление углов этого четырехугольника - очень простая задача, в конце концов, они равны 4 равным углам. Мы видели, что в случае прямоугольников сумма их углов будет равна 360 °, но у нас будет только четырехугольник прямоугольника?
Во-первых, мы должны нарисовать любой четырехугольник, если у него нет всех четырех прямых углов. Чтобы найти сумму внутренних углов этого прямоугольника, необходимо разделить ее, соединяя две вершины, которые не являются соседями, с этим мы получим два треугольника, поэтому просто добавим углы этих двух треугольников и получим результат суммы внутренних углов четырехугольника. На рисунке 2 показано, что мы сказали.
- Расстояние между большими сторонами параллелограмма равно меньшей диагонали. Расстояние между меньшими его сторонами равно большей диагонали.
- Сумма квадратоа диагоналей параллелограмма равна сумме квадратов всех его сторон.
Биссектриса параллелограмма отсекает от него равнобедренный треугольник, основанием которого явяется она сама.
Биссектрисы двух соседних углов параллелограмма взаимно перпендикулярны.
Биссектрисы противоположных углов параллелограмма параллельны или совпадают.
Угол между высотами, проведенными из вершины тупого угла, равен острому углу параллелограмма. Угол между высотами, проведенными из вершины острого угла, равен его тупому углу.
Помните ли вы сумму внутренних углов треугольника? Сумма внутренних углов любого треугольника равна 180 °, т.е. как треугольник 1, так и треугольник 2 имеют сумму своих внутренних углов, равную 180 °, а сумма этих двух треугольников приводит к углам четырехугольника.
Теперь просто выполните следующее. С этим можно заключить, что независимо от выпуклого четырехугольника сумма его внутренних углов будет равна 360 °. Чтобы проверить, попали ли вы, узнайте, каким должен быть угол следующего четырехугольника. Многоугольник из четырех вершин называется четырехугольник. Его вершины отмечены последовательными заглавными буквами в алфавите, против часовой стрелки. Затем стороны пронумерованы строчными буквами с той же буквой, что и верхняя часть, на которую они указывают.
13. Признаки параллелограмма.
- Если у четырехугольника диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
- Если у четырехугольника противолежащие стороны (углы) попарно равны, то этот четырехугольник - параллелограмм.
- Если у четырехугольника две противолежащие стороны и параллельны, и равны, то этот четырехугольник - параллелограмм.
14. Ромб.
Точечный и касательный четырехугольник
Четырехугольник, который может быть ограничен кругом, называется хордой. Для него сумма противоположных углов составляет 180 градусов. Это можно доказать, например, свойствами круговых дуг. Если круговой круг можно вписать, он называется касательным. Для этого суммы длин, обращенных друг к другу, равны. Можно доказать пример свойств точек, проходящих по окружности. Если четырехугольник описывается как круг, круг называется двусторонним.
Мы разделяем квадранты в соответствии с параллелями противоположных сторон. Трапециевидные трапеции и параллелизм. . Четырехугольник - четырехугольник, который не имеет пары противоположных сторон. Это общий случай четырехугольника. Частным случаем дивертикула является дельтоид, имеющий две пары смежных сторон одинаковой длины. Его диагонали перпендикулярны друг другу, и один проходит через центр другого. Кроме того, дельтоид представляет собой касательный четырехугольник. Это является следствием того, что основная диагональ является одновременно осью обоих углов на вершинах, на которых она возникает.
Ромб это параллелограмм, укоторого все стороны равны.
15. Свойства ромба.
- Диагонали ромба взаимно перпендикулярны.
- Диагонали ромба являются биссектрисами его углов.
16. Признаки ромба.
- Так как ромб это параллелограмм, то он обладает всеми свойствами параллелограмма
- Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм является ромбом.
- Если у параллелограмма диагонали являются биссектрисами его углов, то этот параллелограмм является ромбом.
17. Прямоугольник.
Параллелограмма: четырехугольник с противоположными сторонами, параллельный два на два. В параллелограмме диагонали делятся на конгруэнтные части. Если в четырехугольника противоположные стороны конгруэнтны два на два, то четырехугольник является параллелограммом; - если в четырехугольника две противоположные стороны параллельны и конгруэнтны, то четырехугольник является параллелограммом; - если в квадранте диагонали делятся на конгруэнтные части, то четырехугольник является параллелограммом.
Частные случаи четырехугольников
Прямоугольник: параллелограмм с прямым углом. Свойства: в прямоугольнике диагонали конгруэнтны; Прямоугольник имеет две оси симметрии. Свойства: все свойства парограммы верны; - в алмазе диагонали перпендикулярны и являются биссектрисой углов алмаза; Бриллианты алмаза - это оси симметрии.
Прямоугольник это параллелограмм, у которого все углы равные.
18. Свойства прямоугольника.
- Так как прямоугольник это параллелограмм, то он обладает всеми свойствами параллелограмма
- Диагонали прямоугольника равны.
19. Признаки прямоугольника.
- Если у параллелограмма диагонали равны, то он - прямоугольник.
- Если у четырехугольника три угла прямые, то он - прямоугольник.
- Если у параллелограмма один угол прямой, то он - прямоугольник.
20. Квадрат.
Площадь: Квадрат: это двусторонняя прилегающая конгруэнтная сторона или правая ромба. Свойства: -все свойства параллелограмма, алмаза и прямоугольника; Пол имеет четыре оси симметрии. Свойства: - Средняя линия - сегмент, соединяющий беспрецедентные стороны трапеции.
Прямоугольная трапеция: прямой угол - две параллельные стороны. Предупреждение. Вышеприведенный текст является лишь предварительным просмотром отчета, чтобы узнать, может ли помочь содержание этого отчета. Для версии для печати, которая может содержать изображения или таблицы, нажмите кнопку загрузки.
- Квадрат - это параллелограмм, укоторого все стороны равны и все углы равны.
- Квадрат - это прямоугольник, у которого все стороны равны.
- Квадрат - это ромб, у которого все углы равны.
21. Свойства квадрата.
Квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба. Своих собственных свойств у него нет.
Свойства параллелограмма
Выпуклый четырехугольник с параллельными противоположными сторонами называется параллелограммом.
Связанные с боком свойства
Теорема: в параллелограмме. Взаимная теорема 1: если в выпуклом четырехстороннем направлении противоположные стороны конгруэнтны два на два, то четырехугольник является параллелограммом.Угловые свойства
Взаимная теорема 2: если в выпуклом четырехугольника две противоположные стороны параллельны и конгруэнтны, то четырехугольник является параллелограммом. Теорема. В параллелограмме любые два противоположных угла конгруэнтны, и любые два последовательных угла являются дополнительными.
22. Признаки квадрата.
- Если у ромба диагонали равны, то он - квадрат.
- Если у прямоугольника диагонали взаимно перпендикулярны, то он - квадрат.
- Если у прямоугольника диагонали являются биссектрисами его углов, то он - квадрат.
23. Теорема Фалеса.
24. Теорема о пропорциональных отрезках.
Свойства, связанные с диагоналями
Взаимная теорема. Если в выпуклом квадранте противоположные углы конгруэнтны, то четырехугольник является параллелограммом. Если в выпуклом квадранте диагональ имеет такое же среднее значение, то четырехугольник является параллелограммом. Прямоугольник, алмаз, квадрат.
Параллелограмм с прямым углом называется прямоугольником. В прямоугольнике все углы конгруэнтны, так прямые. Если выпуклый четырехугольник имеет все конгруэнтные углы, то он является прямоугольником. В прямоугольнике диагонали конгруэнтны. Если параллелограмм имеет конгруэнтные диагонали, то это прямоугольник. Параллелограмм, имеющий две конгруэнтные последовательные стороны, называется алмазом.
25. Свойство биссектрисы угла треугольника.
26. Средняя линия треугольника.
27. Свойства средней линии треугольника.
28. Теорема Вариньона.
29. Основное свойство медиан треугольника.
30. Трапеция.
31. Высота трапеции.
32. Свойство углов трапеции.
33. Средняя линия трапеции.
34. Свойства средней линии трапеции.
35. Прямоугольная трапеция.
36. Равнобокая трапеция.
37. Свойство диагоналей равнобокой трапеции.
38. Свойство углов равнобокой трапеции.
39. Теорема о высоте равнобокой трапеции, диагонали которой взаимно перпендикулярны.
40. Чему равны отрезки, заключенные между вершинами острых углов и основанием высоты из вершины тупого угла?
41. Признаки равнобокой трапеции.
42. Центральный угол.
43. Вписанный угол.
44. Соответствующие друг другу вписанный и центральный углы.
45. Теорема о вписанном угле.
46. Теорема о вписанных углах, опирающихся на одну дугу.
47. Теорема о вписанном угле, опирающемся на диаметр.
48. Теорема о диаметре, делящем хорду пополам.
49. Чему равен угол между касательной и хордой, проходящей через точку касания?
50. Чему равен угол с вершиной внутри окружности?
51. Чему равен угол между секущими?
52. Чему равен угол между касательными?
53. Чему равен угол между касательной и секущей?
54. Четырехугольник, вписанный в окружность.
55. Где находится центр окружности, описанной около четырехугольника?
56. Четырехугольник, описанный вокруг окружности.
57. Где находится центр окружности, вписанной в четырехугольник?
58. Свойство углов вписанного четырехугольника.
59. Признак вписанного четырехугольника.
60. Свойство сторон описанного четырехугольника.
61. Признак описанного четырехугольника.
62. Теорема Птолемея.
63. Центр окружности, описанной около прямоугольного треугольника.
64. Центр окружности, описанной около прямоугольника.
65. Центр окружности, вписанной в ромб.
66. Под каким углом видна боковая сторона трапеции, описанной около окружности, из центра этой окружности?
67. Подобные треугольники.
68. Какая связь между подобием и равенством треугольников?
69. Коэффициент подобия.
70. Свойства подобный треугольников.
71. Признаки подобия треугольников.
72. Теорема о прямой, параллельной стороне треугольника и пересекающей две другие его стороны.
73. Признаки подобия прямоугольных треугольников.
74. Теорема о подобии в трапеции.
75. Прямоугольный треугольник и его элементы.
76. Теорема о среднем пропорциональном в прямоугольном треугольнике.
77. Теорема о пересекающихся хордах.
78. Теорема об отрезках касательных.
79. Теорема об отрезках секущих.
80. Теорема об отрезках касательной и секущей.
81. Многоугольник.
82. Диагональ многоугольника.
83. Теорема о сумме углов многоугольника.
84. Многоугольник, вписанный в окружность.
85. Многоугольник, описанный вокруг окружности.
86. Где находится центр окружности, вписанной в многоугольник?
87. Где находится центр окружности, описанной вокруг многоугольника?
88. Площадь прямоугольника.
89. Площадь квадрата.
90. Площадь прямоугольного треугольника.
91. Чему равно отношение площадей подобных треугольников?
92. Площадь параллелограмма.
93. Площадь ромба.
94. Площадь треугольника.
95. Площадь трапеции.
96. Площадь четырехугольника со взаимно перпендикулярными сторонами.
97. Площадь трапеции, описанной около окружности.
98. Теорема Пифагора.
99. Следствия из теоремы Пифагора.
100. Теорема, обратная теореме Пифагора.
101. Египетский треугольник.
102. Перпендикуляр и наклонная.
103. Проекция наклонной на прямую.
104. Свойства наклонных и их проекций.
105. Чему равен квадрат диагонали прямоугольника?
106. Теорема о сумме квадратов диагоналей параллелограмма.
107. Теорема о сумме квадратов диагоналей трапеции.
108. Синус острого угла прямоугольного треугольника.
109. Косинус острого угла прямоугольного треугольника.
110. Тангенс острого угла прямоугольного треугольника.
111. Котангенс острого угла прямоугольного треугольника.
112. Катет, противолежащий углу а, равен ………….. или …………………
113. Катет, прилежащий к углу а, равен ………………или …………………
114. Значения синусов основных углов.
115. Значения косинусов основных углов.
116. Значения тангенсов основных углов.
117. Значения котангенсов основных углов.
118. Как изменяются синус, косинус и тангенс острого угла с его увеличением?
119. Формулы дополнения.
Определения
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Диагональ четырехугольника – отрезок, соединяющий любые две несоседние вершины.
Различают выпуклые и невыпуклые четырехугольники.
Четырехугольник называется выпуклым, если он находится в одной полуплоскости относительно прямой, содержащей любую его сторону.
В школьном курсе рассматриваются только выпуклые четырехугольники. Поэтому далее “выпуклый четырехугольник” будем сокращенно называть “четырехугольник”.
Теорема
Сумма внутренних углов любого четырехугольника равна \(360^\circ\) .
Доказательство

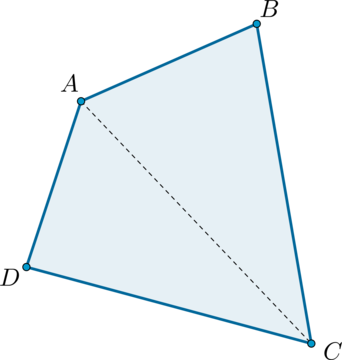
Рассмотрим четырехугольник \(ABCD\) и проведем его диагональ \(AC\) . Она разбила четырехугольник на два треугольника. Сумма углов любого треугольника равна \(180^\circ\) , следовательно:
\[\begin{multline*} 360^\circ=180^\circ+180^\circ=(\angle DAC+\angle D+\angle ACD) + (\angle CAB+\angle B+\angle ACB)=\\ =\angle D+\angle B +(\angle DAC+\angle CAB)+(\angle ACD+\angle ACB)=\angle D+\angle B+\angle A+\angle C \end{multline*}\]
Теорема Вариньона
Выпуклый четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом.
Доказательство*
С доказательством данной теоремы рекомендуется ознакомиться после изучения темы “Средняя линия треугольника”.
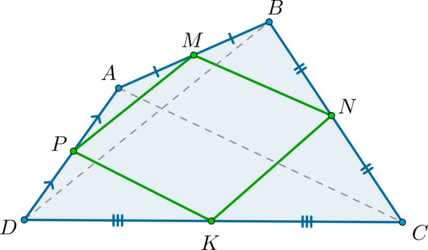
Проведем диагонали четырехугольника \(ABCD\) . Рассмотрим \(\triangle ABC\) : \(MN\) – средняя линия этого треугольника, следовательно, \(MN\parallel AC\) .
Рассмотрим \(\triangle ADC\) : \(PK\) – средняя линия этого треугольника, следовательно, \(PK\parallel AC\) .
Таким образом, \(MN\parallel AC\parallel PK\) .
Аналогичным образом доказывается, что \(MP\parallel BD\parallel NK\) .
Следовательно, по определению \(MNKP\) – параллелограмм.
Теорема
Если в четырехугольнике \(ABCD\) диагонали взаимно перпендикулярны, то суммы квадратов противоположных сторон равны: \
Доказательство
По теореме Пифагора:
\[\begin{aligned} &AB^2=x^2+a^2\\ &CD^2=b^2+y^2\\ &BC^2=x^2+b^2\\ &AD^2=a^2+y^2 \end{aligned}\]
Из равенств видно, что \(AB^2+CD^2=x^2+a^2+y^2+b^2=BC^2+AD^2\)
Замечание
Все известные четырехугольники, изучаемые в школьной программе, подчиняются следующей схеме:
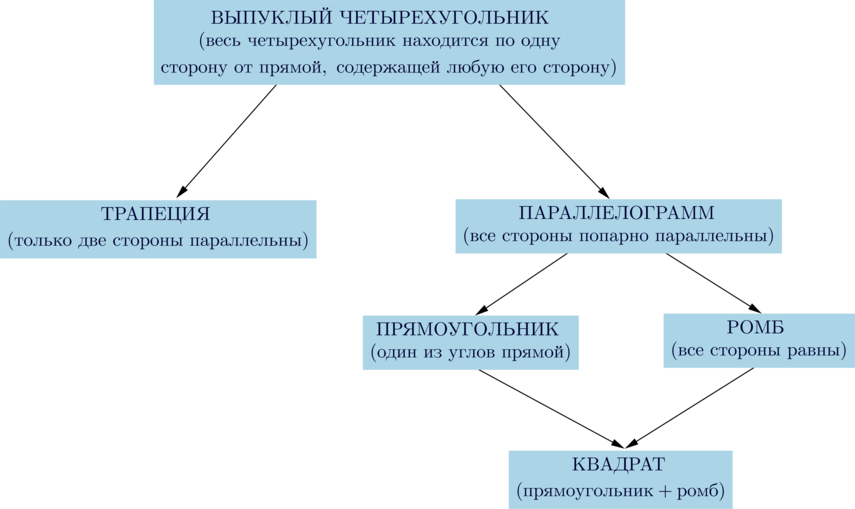
Таким образом, любой четырехугольник из этой схемы обладает свойствами всех предыдущих четырехугольников, из которых он следует.
Например, прямоугольник обладает свойствами параллелограмма и произвольного выпуклого четырехугольника; квадрат обладает свойствами прямоугольника, параллелограмма, выпуклого четырехугольника.
- Зависимость скорости ферментативной реакции от температуры, pH и времени инкубации Как влияет температура на рн
- Зависимость скорости ферментативной реакции от температуры, pH и времени инкубации Ph от температуры
- Святые богоотцы иоаким и анна Иоаким и анна когда почитание
- Храм святой великомученицы екатерины в риме
- Численность последователей основных религий и неверующих
- Абсолютные и относительные координаты Что называется абсолютными координатами точек
- Какие меры относились к политике военного коммунизма

 Live Journal
Live Journal Facebook
Facebook Twitter
Twitter