Многочлены и их корни. Методы разложения многочленов на множители. Проверка домашнего задания

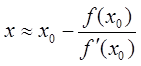
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

СУМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

КАФЕДРА ИНФОРМАТИКИ

Контрольная работа

ПО ЧИСЛЕННЫМ МЕТОДАМ

на тему:

“ Метод ы нахождения корней полиномов”

2 Схема Горнера

3 Функции произвольного вида

4 Нахождение корней полиномов

Список используемых информационных источников

1 Нахождение корней уравнений (Equation Section 1)

Одним из наиболее распространенных методов поиска корней уравнений является метод Ньютона и его модификации. Пусть требуется решить уравнение

. Будем считать, что x является решением уравнения. Разложим функцию f(x) в ряд в точке x0 близкой к точке x и ограничимся только первыми двумя членами разложения.

Поскольку x – корень уравнения, то

. Следовательно,

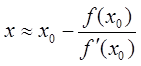
Таким образом, если нам известно приближенное значение корня уравнения, то полученное уравнение позволяет его уточнить. Понятно, что процесс уточнения можно повторять многократно, до тех пор, пока значение функции не будут отличаться от нуля на величину меньшую, чем заданная точность поиска. Очередное k-е приближение находится по формуле

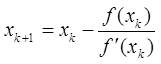
Ограничившись в разложении только первыми двумя членами, мы фактически заменили функцию f(x) на прямую линию, касательную в точке x0, поэтому метод Ньютона еще называют методом касательных. Далеко не всегда бывает удобно находить аналитическое выражение для производной функции. Однако, в этом и нет особой необходимости: поскольку на каждом шаге мы получаем приближенное значение корня, можно для его вычисления использовать приближенное значение производной.

В качестве малой величины

можно взять, например, заданную точность вычислений , тогда расчетная формула примет вид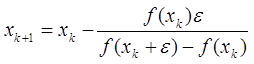 (1.1)

С другой стороны, для вычисления производной можно воспользоваться значениями функции, полученными на двух предыдущих шагах,

(1.2)

В таком виде метод называется методом секущих (secantmethod). При этом, однако, возникает проблема с вычислением первого приближения. Обычно полагают, что

, то есть первый шаг вычислений проводится с использованием формулы (1.1), а все последующие – с использованием формулы (1.2). Именно эта вычислительная схема реализована в пакете Mathcad. Используя метод секущих, мы не можем гарантировать, что корень находится между двумя последними приближениями. Можно, однако, для вычисления очередного приближения использовать границы интервала, на котором функция меняет знак. Такой метод называется методом хорд (falsepositionmethod).

Идея метода секущих развивается в методе Мюллера. Однако в этом методе для нахождения очередного приближения используются три предыдущие точки. Иными словами, метод использует не линейную, а квадратичную интерполяцию функции. Расчетные формулы метода следующие :

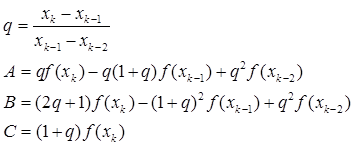(1.3)

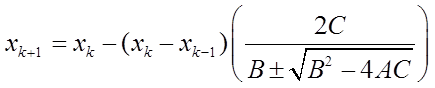(1.4)

Знак перед корнем выбирается так, чтобы абсолютное значение знаменателя было максимальным.

Поскольку поиск корня заканчивается, когда выполнится условие

, то возможно появление ложных корней. Например, для уравнения ложный корень появится в том случае, если точность поиска задана меньше, чем 0,0001. Увеличивая точность поиска, можно избавиться от ложных корней. Однако не для всех уравнений такой подход работает. Например, для уравнения , которое, очевидно, не имеет действительных корней, для любой, сколь угодно малой точности найдется значение x, удовлетворяющее критерию окончания поиска. Приведенные примеры показывают, что к результатам компьютерных вычислений всегда нужно относиться критически, анализировать их на правдоподобность. Чтобы избежать "подводных камней" при использовании любого стандартного пакета, реализующего численные методы, нужно иметь хотя бы минимальное представление о том, какой именно численный метод реализован для решения той или иной задачи.

В том случае, когда известен интервал, на котором расположен корень, можно воспользоваться иными методами нахождения решения уравнения.

В методе Риддера (Ridder’smethod) вычисляют значение функции в середине интервала

. Затем ищут экспоненциальную функцию такую, что Затем применяют метод хорд, используя значения . Очередное значение вычисляют по формуле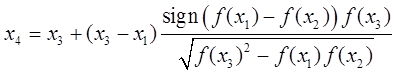

(1.5)

Метод Брента (Brentmethod) соединяет быстроту метода Риддера и гарантированную сходимость метода деления отрезка пополам. Метод использует обратную квадратичную интерполяцию, то есть ищет x как квадратичную функцию y. На каждом шаге проверяется локализация корня. Формулы метода достаточно громоздки и мы не будем их приводить.

Особые методы применяют для поиска корней полинома. В этом случае могут быть найдены все корни. После того как один из корней полинома найден, степень полинома может быть понижена, после чего поиск корня повторяется.

Метод Лобачевского, метод приближённого (численного) решения алгебраических уравнений, найденный независимо друг от друга бельгийским математиком Ж. Данделеном, русским математиком Н. И. Лобачевским (в 1834 в наиболее совершенной форме) и швейцарским математиком К. Греффе. Суть Л. м. состоит в построении уравнения f1(x) = 0, корни которого являются квадратами корней исходного уравнения f(x) = 0. Затем строят уравнение f2(x) = 0, корнями которого являются квадраты корней уравнения f1(x) = 0. Повторяя этот процесс несколько раз, получают уравнение, корни которого сильно разделены. В случае если все корни исходного уравнения действительны и различны по абсолютной величине, имеются простые вычислительные схемы Л. м. для нахождения приближённых значений корней. В случае равных по абсолютной величине корней, а также комплексных корней вычислительные схемы Л. м. очень сложны.

Метод Лагерра (Laguerre’smethod) основывается на следующих соотношениях для полиномов

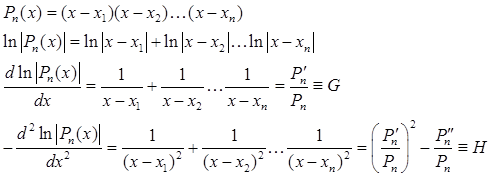
Предполагают, что корень x1 находится на расстоянии a от текущего приближения, в то время как все другие корни находятся на расстоянии b:

. Тогда ,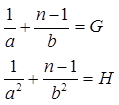

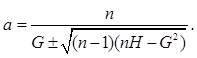
Знак перед корнем выбирают с таким расчетом, чтобы получить наибольшее значение знаменателя.

Еще один метод, который применяют для поиска корней полиномов, – метод сопровождающей матрицы (companionmatrix). Можно доказать, что матрица

,

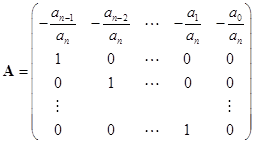называемая сопровождающей матрицей для полинома

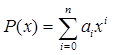, имеет собственные значения равные корням полинома. Напомним, что собственными значениями матрицы называются такие числа , для которых выполняется равенство или . Существуют весьма эффективные методы поиска собственных значений, о некоторых из них мы будем говорить далее. Таким образом, задачу поиска корней полинома можно свести к задаче поиска собственных значений сопровождающей матрицы.

2 Схема Горнера

Вычисление по схеме Горнера оказывается более эффективным, причем оно не очень усложняется. Эта схема основывается на следующем представлении многочлена:

p(x) = ((... ((anx + an-1)x + an-2)x + ... + a2)x + a1)x + a0.

Займемся общим многочленом вида:

p(x) = anxn + an-1xn-1 + an-2xn-2 + ... + a2x2 + a1x + a0.

Мы будем предполагать, что все коэффициенты an, ..., a0 известны, постоянны и записаны в массив. Это означает, что единственным входным данным для вычисления многочлена служит значение x, а результатом программы должно быть значение многочлена в точке x.
Стандартный алгоритм вычисления прямолинеен:

Evaluate(x)xточка, в которой вычисляется значение многочлена result = a + a*xxPower = xfor i = 2 to n doxPower = xPower*xresult = result + a[i]*xPowerend forreturn result

Этот алгоритм совершенно прозрачен и его анализ очевиден. В цикле for содержится два умножения, которые выполняются n - 1 раз. Кроме того, одно умножение выполняется перед циклом, поэтому общее число умножений равно 2n - 1. В цикле выполняется также одно сложение, и одно сложение выполняется перед циклом, поэтому общее число сложений равно n.

Вы можете легко проверить, что это представление задает тот же многочлен, что и выше. Соответствующий алгоритм выглядит так:

HornersMethod(x)xточка, в которой вычисляется значение многочленаfor i = n - 1 down to 0 doresult = result*xresult = result + a[i]end forreturn result

Цикл выполняется n раз, причем внутри цикла есть одно умножение и одно сложение. Поэтому вычисление по схеме Горнера требует n умножениё и n сложений - двукратное уменьшение числа умножений по сравнению со стандартным алгоритмом.

Предварительная обработка коэффициентов

Результат можно даже улучшить, если обработать коэффициенты многочлена до начала работы алгоритма. Основная идея состоит в том, чтобы выразить многочлен через многочлены меньшей степени. Например, для вычисления значения x256 можно воспользоваться таким же циклом, как и в функции Evaluate в начале этой статьи; в результате будет выполнено 255 умножений. Альтернативный подход состоит в том, чтобы положить result = x*x, а затем семь раз выполнить операцию result = result*result. После первого выполнения переменная result будет содержать x4, после второго x8, после третьего x16, после четвертого x32, после пятого x64, после шестого x128, и после седьмого x256.

Для того, чтобы метод предварительной обработки коэффициентов работал, нужно, чтобы многочлен был унимодальным (то есть старший коэффициент an должен равняться 1) , а степень многочлена должна быть на единицу меньше некоторой степени двойки (n = 2k - 1 для некоторого k > 1). В таком случае многочлен можно представить в виде:

p(x) = (xj + b)q(x) + r(x), где j = 2k-1. (1)

В обоих многочленах q и r будет вдвое меньше членов, чем в p. Для получения нужного результата мы вычислим по отдельности q(x) и r(x), а затем сделаем одно дополнительное умножение и два сложения. Если при этом правильно выбрать значение b, то оба многочлена q и r оказываются унимодальными, причем степень каждого из них позволяет применить к каждому из них ту же самую процедуру. Мы увидим, что ее последовательное применение позволяет сэкономить вычисления.

Вместо того, чтобы вести речь о многочленах общего вида, обратимся к примеру. Рассмотрим многочлен:

p(x) = x7 + 4x6 - 8x4 + 6x3 + 9x2 + 2x - 3.

Определим сначала множитель xj + b в уравнении (1). Степень многочлена p равна 7, то есть 23 - 1, поэтому k = 3. Отсюда вытекает, что j = 22 = 4. Выберем значение b таким образом, чтобы оба многочлена q и r были унимодальными. Для этого нужно посмотреть на коэффициенты aj-1 в p и положить b = aj-1 - 1. В нашем случае это означает, что b = a3 - 1 = 5. Теперь мы хотим найти значения q и r, удовлетворяющие уравнению:

x7 + 4x6 - 8x4 + 6x3 + 9x2 + 2x - 3 = (x4 + 5)q(x) + r(x).

Многочлены q и r совпадают соответственно с частным и остатком от деления p на x4 + 5. Деление с остатком дает:

p(x) = (x4 + 5)(x3 + 4x2 + 0x + 8) + (x3 - 11x2 + 2x - 37).

На следующем шаге мы можем применить ту же самую процедуру к каждому из многочленов q и r:

q(x) = (x2 - 1)(x + 4) + (x + 12), r(x) = (x2 + 1)(x - 11) + (x - 26).

В результате получаем:

p(x) = (x4 + 5)((x2 - 1)(x + 4) + (x + 12)) + ((x2 + 1)(x - 11) + (x - 26)).

Посмотрев на этот многочлен, мы видим, что для вычисления x2 требуется одно умножение; еще одно умножение необходимо для подсчета x4 = x2*x2. Помимо этих двух умножений в вычислении правой части равенства участвуют еще три умножения. Кроме того, выполняется 10 операций сложения. В таблице 1 приведены сравнительные результаты анализа этого метода и других методов вычисления. Экономия не выглядит значительной, однако это объясняется тем, что мы рассматриваем лишь частный случай. Общую формулу для сложности можно вывести, внимательно изучив процедуру. Заметим прежде всего, что в равенстве (1) участвуют одно умножение и два сложения. Поэтому для числа умножений M = M(k) и числа сложений A = A(k) мы получаем следующий набор рекуррентных соотношений:

Решая эти соотношения, мы заключаем, что число умножений приблизительно равно N/2, а число сложений приблизительно равно (3N - 1)/2. Неучтенными, однако, остались умножения, необходимые для подсчета последовательности значений x2, x4, x8, ..., x2k-1; на это требуется дополнительно k - 1 умножение. Поэтому общее число умножений приблизительно равно N/2 + log2N.

Таблица 2. Число операций при вычислении значения многочлена степени N

В таблице 2 приведены результаты сравнительного анализа стандартного алгоритма, схемы Горнера и алгоритма с предварительной обработкой коэффициентов. При сравнении последних двух алгоритмов видно, что нам удалось сэкономить N/2 - log2N умножений, но за счет дополнительных (N - 1)/2 сложений. Во всех существующих вычислительных системах обмен умножений на сложения считается выгодным, поэтому предварительная обработка коэффициентов повышает эффективность.

3 Функции произвольного вида

Найдем нули функции

на интервале x=[–2,7], используя Mathcad

Изобразим сначала функцию на графике.

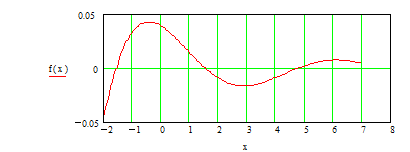
На заданном интервале функция три раза обращается в ноль. Определим нули функции, используя встроенную функцию root(f(x),x). Первый аргумент – функция, нуль которой необходимо найти, второй – переменная, которую необходимо варьировать. (Вообще говоря, функция f может быть функцией многих переменных и необходимо указывать, по какой именно переменной мы ищем нуль функции.) Кроме того, необходимо задать начальное приближение поиска. Точность вычислений задается встроенной переменной TOL. По умолчанию ее значение равно 0,001. Это значение можно изменить либо через меню Math/Built–In Variables или непосредственно в тексте документа:

Задаем начальное приближение:

И вычисляем корень:

Если требуется найти несколько корней, как в нашей задаче, то имеет смысл определить новую функцию.

Доказано, что для разложения многочлена на множители, нужно найти его корни. Формулы корней квадратного многочлена. Метод нахождения целых корней. Метод разложения на множители биквадратного многочлена и приводящихся к квадратным. Возвратные многочлены.

Основа метода

Пусть

- многочлен степени n ≥ 1 от действительной или комплексной переменной z с действительными или комплексными коэффициентами a i . Примем без доказательства следующую теорему.

Теорема 1

Уравнение P n (z) = 0 имеет хотя бы один корень.

Докажем следующую лемму.

Лемма 1

Пусть P n (z) - многочлен степени n , z 1 - корень уравнения:
P n (z 1) = 0 .
Тогда P n (z) можно представить единственным способом в виде:
P n (z) = (z - z 1) P n-1 (z) ,
где P n-1 (z) - многочлен степени n - 1 .

Доказательство

Для доказательства, применим теорему (см. Деление и умножение многочлена на многочлен уголком и столбиком), согласно которой для любых двух многочленов P n (z) и Q k (z) , степеней n и k , причем n ≥ k , существует единственное представление в виде:
P n (z) = P n-k (z) Q k (z) + U k-1 (z) ,
где P n-k (z) - многочлен степени n-k , U k-1 (z) - многочлен степени не выше k-1 .

Положим k = 1 , Q k (z) = z - z 1 , тогда
P n (z) = (z - z 1 ) P n-1 (z) + c ,
где c - постоянная. Подставим сюда z = z 1 и учтем, что P n (z 1) = 0 :
P n (z 1 ) = (z 1 - z 1 ) P n-1 (z 1 ) + c ;
0 = 0 + c .
Отсюда c = 0 . Тогда
P n ,
что и требовалось доказать.

Разложение многочлена на множители

Итак, на основании теоремы 1, многочлен P n (z) имеет хотя бы один корень. Обозначим его как z 1 , P n (z 1) = 0 . Тогда на основании леммы 1:
P n (z) = (z - z 1 ) P n-1 (z) .
Далее, если n > 1 , то многочлен P n-1 (z) также имеет хотя бы один корень, который обозначим как z 2 , P n-1 (z 2) = 0 . Тогда
P n-1 (z) = (z - z 2 ) P n-2 (z) ;
P n (z) = (z - z 1 )(z - z 2 ) P n-2 (z) .

Продолжая этот процесс, мы приходим к выводу, что существует n чисел z 1 , z 2 , ... , z n таких, что
P n (z) = (z - z 1 )(z - z 2 ) ... (z - z n ) P 0 (z) .
Но P 0 (z) - это постоянная. Приравнивая коэффициенты при z n , находим что она равна a n . В результате получаем формулу разложения многочлена на множители:
(1) P n (z) = a n (z - z 1 )(z - z 2 ) ... (z - z n ) .

Числа z i являются корнями многочлена P n (z) .

В общем случае не все z i , входящие в (1) , различны. Среди них могут оказаться одинаковые значения. Тогда разложение многочлена на множители (1) можно записать в виде:
(2) P n (z) = a n (z - z 1 ) n 1 (z - z 2 ) n 2 ... (z - z k ) n k ;
.
Здесь z i ≠ z j при i ≠ j . Если n i = 1 , то корень z i называется простым . Он входит в разложение на множители в виде (z-z i ) . Если n i > 1 , то корень z i называется кратным корнем кратности n i . Он входит в разложение на множители в виде произведения n i простых множителей: (z-z i )(z-z i ) ... (z-z i ) = (z-z i ) n i .

Многочлены с действительными коэффициентами

Лемма 2

Если - комплексный корень многочлена с действительными коэффициентами, , то комплексно сопряженное число также является корнем многочлена, .

Доказательство

Действительно, если , и коэффициенты многочлена - действительные числа, то .

Таким образом, комплексные корни входят в разложение на множителями парами со своими комплексно сопряженными значениями:
,
где , - действительные числа.
Тогда разложение (2) многочлена с действительными коэффициентами на множители можно представить в виде, в котором присутствуют только действительные постоянные:
(3) ;
.

Методы разложения многочлена на множители

С учетом сказанного выше, для разложения многочлена на множители, нужно найти все корни уравнения P n (z) = 0 и определить их кратность. Множители с комплексными корнями нужно сгруппировать с комплексно сопряженными. Тогда разложение определяется по формуле (3) .

Таким образом, метод разложения многочлена на множители заключается в следующем:
1. Находим корень z 1 уравнения P n (z 1) = 0 .
2.1. Если корень z 1 действительный, то в разложение добавляем множитель (z - z 1) (z - z 1) 1 :
.
1 (z) , начиная с пункта (1) , пока не найдем все корни.
2.2. Если корень комплексный, то и комплексно сопряженное число является корнем многочлена. Тогда в разложение входит множитель

,
где b 1 = - 2 x 1 , c 1 = x 1 2 + y 1 2 .
В этом случае, в разложение добавляем множитель (z 2 + b 1 z + c 1) и делим многочлен P n (z) на (z 2 + b 1 z + c 1) . В результате получаем многочлен степени n - 2 :
.
Далее повторяем процесс для многочлена P n-2 (z) , начиная с пункта (1) , пока не найдем все корни.

Нахождение корней многочлена

Главной задачей, при разложении многочлена на множители, является нахождение его корней. К сожалению, не всегда это можно сделать аналитически. Здесь мы разберем несколько случаев, когда можно найти корни многочлена аналитически.

Корни многочлена первой степени

Многочлен первой степени - это линейная функция. Она имеет один корень. Разложение имеет только один множитель, содержащий переменную z :
.

Корни многочлена второй степени

Чтобы найти корни многочлена второй степени, нужно решить квадратное уравнение:
P 2 (z) = a 2 z 2 + a 1 z + a 0 = 0 .
Если дискриминант , то уравнение имеет два действительных корня:
, .
Тогда разложение на множители имеет вид:
.
Если дискриминант D = 0 , то уравнение имеет один двукратный корень:
;
.
Если дискриминант D < 0 , то корни уравнения комплексные,
.

Многочлены степени выше второй

Существуют формулы для нахождения корней многочленов 3-ей и 4-ой степеней. Однако ими редко пользуются, поскольку они громоздкие. Формул для нахождения корней многочленов степени выше 4-ой нет. Несмотря на это, в некоторых случаях, удается разложить многочлен на множители.

Нахождение целых корней

Если известно, что многочлен, у которого коэффициенты - целые числа, имеет целый корень, то его можно найти, перебрав все возможные значения.

Лемма 3

Пусть многочлен
,
коэффициенты a i которого - целые числа, имеет целый корень z 1 . Тогда этот корень является делителем числа a 0 .

Доказательство

Перепишем уравнение P n (z 1) = 0 в виде:
.
Тогда - целое,
M z 1 = - a 0 .
Разделим на z 1 :
.
Поскольку M - целое, то и - целое. Что и требовалось доказать.

Поэтому, если коэффициенты многочлена - целые числа, то можно попытаться найти целые корни. Для этого нужно найти все делители свободного члена a 0 и, подстановкой в уравнение P n (z) = 0 , проверить, являются ли они корнями этого уравнения.
Примечание . Если коэффициенты многочлена - рациональные числа, , то умножая уравнение P n (z) = 0 на общий знаменатель чисел a i , получим уравнение для многочлена с целыми коэффициентами.

Нахождение рациональных корней

Если коэффициенты многочлена - целые числа и целых корней нет, то при a n ≠ 1 , можно попытаться найти рациональные корни. Для этого нужно сделать подстановку
z = y/a n
и умножить уравнение на a n n-1 . В результате мы получим уравнение для многочлена от переменной y с целыми коэффициентами.Далее ищем целые корни этого многочлена среди делителей свободного члена. Если мы нашли такой корень y i , то перейдя к переменной x , получаем рациональный корень
z i = y i /a n .

Полезные формулы

Приведем формулы, с помощью которых можно разложить многочлен на множители.

В более общем случае, чтобы разложить многочлен
P n (z) = z n - a 0 ,
где a 0 - комплексное, нужно найти все его корни, то есть решить уравнение:
z n = a 0 .
Это уравнение легко решается, если выразить a 0 через модуль r и аргумент φ :
.
Поскольку a 0 не изменится, если к аргументу прибавить 2 π , то представим a 0 в виде:
,
где k - целое. Тогда
;
.
Присваивая k значения k = 0, 1, 2, ... n-1 , получаем n корней многочлена. Тогда его разложение на множители имеет вид:
.

Биквадратный многочлен

Рассмотрим биквадратный многочлен:
.
Биквадратный многочлен можно разложить на множители, без нахождения корней.

При , имеем:

,
где .

Бикубический и многочлены, приводящиеся к квадратному

Рассмотрим многочлен:
.
Его корни определяются из уравнения:
.
Оно приводится к квадратному уравнению подстановкой t = z n :
a 2 n t 2 + a n t + a 0 = 0 .
Решив это уравнение, найдем его корни, t 1 , t 2 . После чего находим разложение в виде:
.
Далее методом, указанным выше, раскладываем на множители z n - t 1 и z n - t 2 . В заключении группируем множители, содержащие комплексно сопряженные корни.

Возвратные многочлены

Многочлен называется возвратным , если его коэффициенты симметричны:

Пример возвратного многочлена:
.

Если степень возвратного многочлена n - нечетна, то такой многочлен имеет корень z = -1 . Разделив такой многочлен на z + 1 , получим возвратный многочлен степени n - 1 .
Если степень возвратного многочлена n - четна, то подстановкой , он приводится к многочлену степени n/2 . См.