Чему равен четырехугольник. По углу и трем сторонам

• Многоуго́льником

  называется геометрическая фигура, состоящая из n

• (n больше или равно 3) точек плоскости, не лежащих на одной прямой и попарно соединённых не пересекающимися отрезками. Многоугольник - это замкнутая ломаная линия. Существуют три различных варианта определения:
• Плоские замкнутые ломаные;
• Плоские замкнутые ломаные без самопересечений;
• Части плоскости, ограниченные ломаными.
• Вершины ломаной называются вершинами многоугольника, а отрезки - сторонами многоугольника.

• Сумма внутренних углов плоского выпуклого n-угольника равна

  (в градусах)

  Узнайте, как ваш ребенок узнает о четырехсторонних, двумерных формах в начальной школе и попробует практические занятия, чтобы укрепить свое обучение дома. Четырехугольник представляет собой четырехстороннюю двумерную форму. Следующие двумерные формы - все четырехугольники: квадрат, прямоугольник, ромб, трапеция, параллелограмма и кайт.

  Что дети учат квадрилатералам в начальной школе?

  В 1-м году дети узнают, например, прямоугольники и квадраты. В 2-м году дети начнут смотреть на квадраты и прямоугольники. Им будет предложено использовать эти фигуры. Они также начнут узнавать и поэтому узнают, что квадраты и прямоугольники имеют четыре прямых угла.

  (в радианах).

• Число диагоналей всякого многоугольника равно n(n − 3) / 2, где n - число сторон.

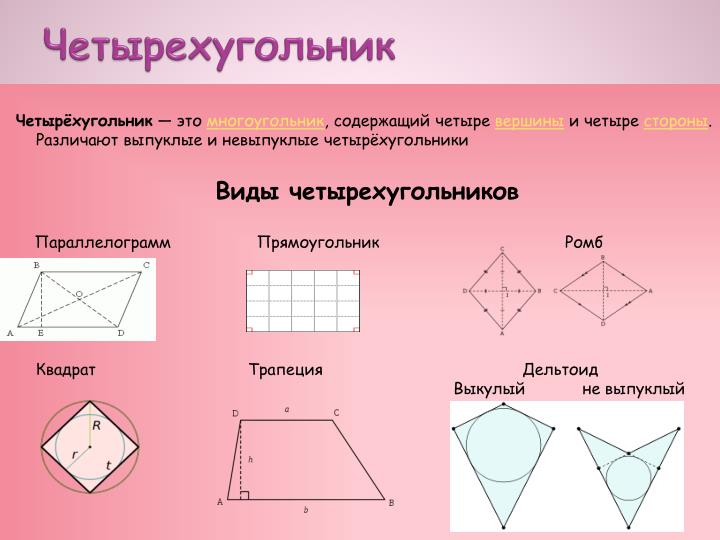
Четырёхугольник - это многоугольник, содержащий четыре вершины и четыре стороны. Различают выпуклые и невыпуклые четырёхугольники

Виды четырехугольников

Параллелограмм Прямоугольник Ромб

Квадрат Трапеция Дельтоид Выкулый не выпуклый

Четырехугольника

• Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
• Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
• Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
• Шесть расстояний между четырьмя произвольными точками плоскости, взятыми попарно, связаны соотношением:

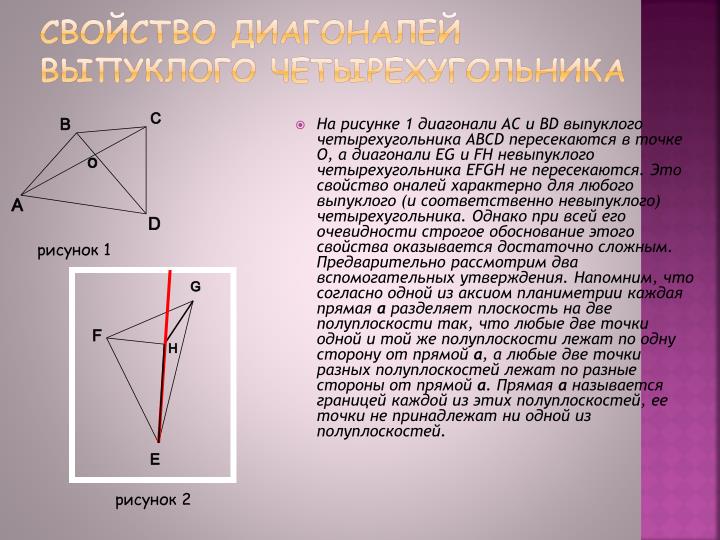
• На рисунке 1 диагонали AC и BD выпуклого четырехугольника ABCD пересекаются в точке O, а диагонали EG и FH невыпуклого четырехугольника EFGH не пересекаются. Это свойство оналей характерно для любого выпуклого (и соответственно невыпуклого) четырехугольника. Однако при всей его очевидности строгое обоснование этого свойства оказывается достаточно сложным. Предварительно рассмотрим два вспомогательных утверждения. Напомним, что согласно одной из аксиом планиметрии каждая прямая а разделяет плоскость на две полуплоскости так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а. Прямая а называется границей каждой из этих полуплоскостей, ее точки не принадлежат ни одной из полуплоскостей.

рисунок 1

рисунок 2

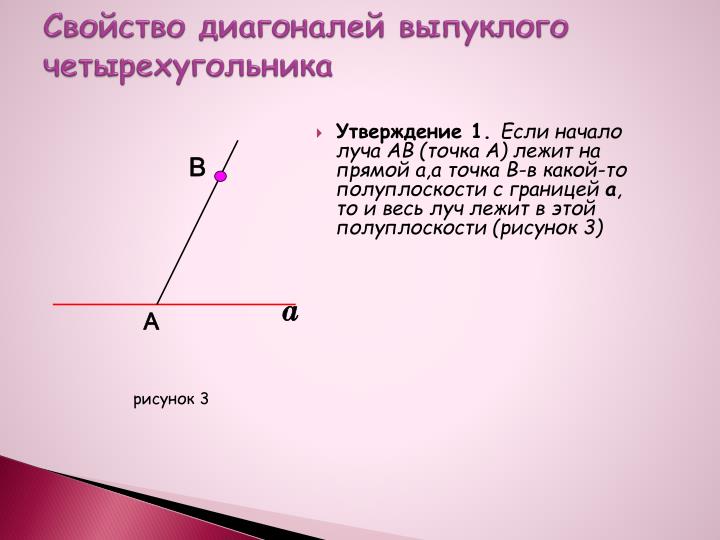
• Утверждение 1. Если начало луча AB (точка A) лежит на прямой а,а точка B-в какой-то полуплоскости с границей а, то и весь луч лежит в этой полуплоскости (рисунок 3)

рисунок 3

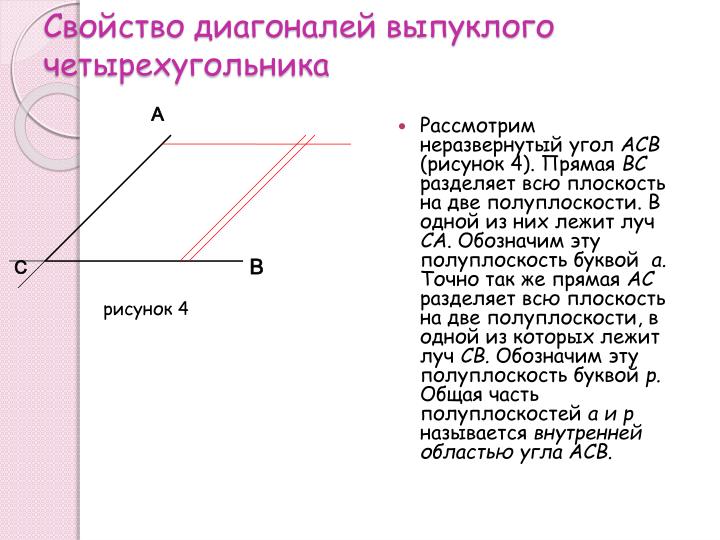
• Рассмотрим неразвернутый угол ACB (рисунок 4). Прямая BC разделяет всю плоскость на две полуплоскости. В одной из них лежит луч CA. Обозначим эту полуплоскость буквой a. Точнотак же прямая AC разделяет всю плоскость на две полуплоскости, в одной из которых лежит луч CB. Обозначим эту полуплоскость буквой p. Общая часть полуплоскостей а и p называется внутренней областью угла ACB.

рисунок 4

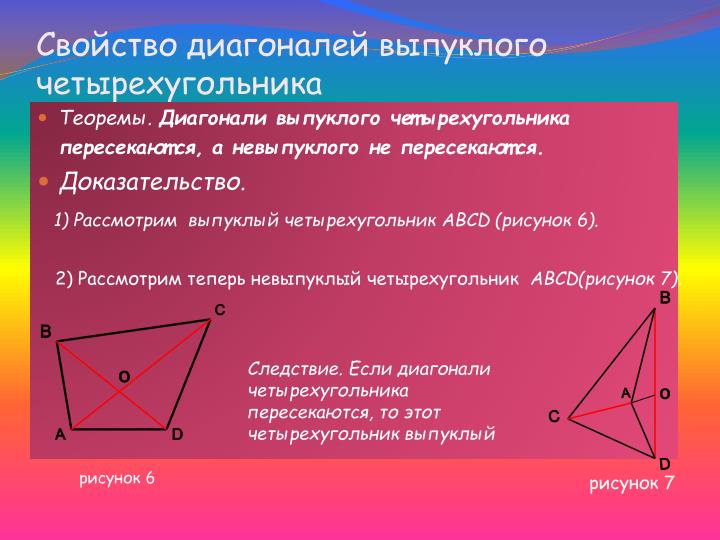
• Утверждение 2. Если точки А и В лежат на разных сторонах неразвернутого угла с вершиной С, а точка D лежит внутри угла АСВ (т.е. в его внутренней области), то луч СD пересекает отрезок АВ (рисунок 5)
• С наглядной точки зрения утверждения 1 и 2 совершенно очевидны.

рисунок 5

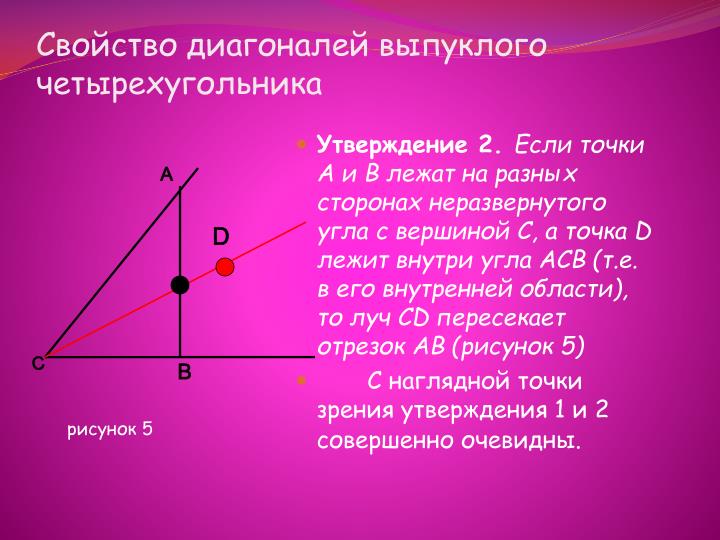
• Теоремы. Диагонали выпуклого четырехугольника пересекаются, а невыпуклого не пересекаются.
• Доказательство.

  1) Рассмотрим выпуклый четырехугольник ABCD (рисунок 6).

  Действие 1: Классификация четырехугольников по функциям

  Это мероприятия, призванные представить некоторые предварительные идеи о математических определениях. Студенты будут делать наблюдения из набора примеров. На этом уровне не ожидается, что студент докажет, что функции следуют из определений. Вы можете скопировать лист для каждого студента или листов ламината для повторного использования. Возможно, вам придется объяснять символы «равно» или «параллельно».

  Студенты разрезают лист, чтобы они могли расположить четырехугольники по группам в соответствии с различными критериями, предложенными учителем или учениками. Число равных сторон число пар равных противоположных сторон число пар параллельных сторон число прямых углов. Например, следующая диаграмма Венна показывает множества квадрилатеров с 0, 1 и 2 парами параллельных сторон.

2) Рассмотрим теперь невыпуклый четырехугольник ABCD(рисунок 7).

Следствие. Если диагонали четырехугольника пересекаются, то этот четырехугольник выпуклый

рисунок 6

рисунок 7

Фигуры

• Утверждение о характеристическом свойстве фигуры можно сформулировать с использованием словосочетания “тогда и только тогда”. Например: диагонали четырехугольника пересекаются тогда и только тогда, когда он является выпуклым.

Площадь произвольного выпуклого четырёхугольника равна:

• , где d1, d2 - диагонали и α - угол между диагоналями.

• , где e, f - длины диагоналей, a, b, c, d - длины сторон.

Где p - полупериметр. Из этой формулы для вписанных 4-угольников следует формула Брахмагупты.

Особые случаи

Если 4-угольник и вписан и описан, то

• Диагонали прямоугольника равны.
• Прямоугольник является параллелограммом - его противоположные стороны параллельны.
• Стороны прямоугольника являются одновременно его высотами.
• Квадрат диагонали прямоугольника равен сумме квадратов двух его не противоположных сторон (по теореме Пифагора).
• Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности.

• Стороны и диагонали
• Длиной прямоугольника называют длину более длинной пары его сторон, а шириной - длину более короткой пары сторон.
• Длина диагонали прямоугольника вычисляется по теореме Пифагора и равна квадратному корню из суммы квадратов длины и ширины.

Фигуры

Площадь ромба

Площадь ромба равна половине произведения его диагоналей.

Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.

• Ромб является параллелограммом. Его противолежащие стороны попарно параллельны, АВ || CD, AD || ВС.
• Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам.
• Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
• Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.

Кроме того площадь ромба может быть вычислена по формуле:

Угол между двумя смежными сторонами ромба.

Прямоугольная трапеция

Равнобокая трапеция

• У равнобедренной трапеции диагонали равны.
• Если трапеция равнобедренная, то около неё можно описатьокружность.
• Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.
• В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон находятся на одной прямой.
• Если у равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
• Если сумма углов при любом основании трапеции равна 90°, то отрезок соединяющий середины оснований равен их полуразности.

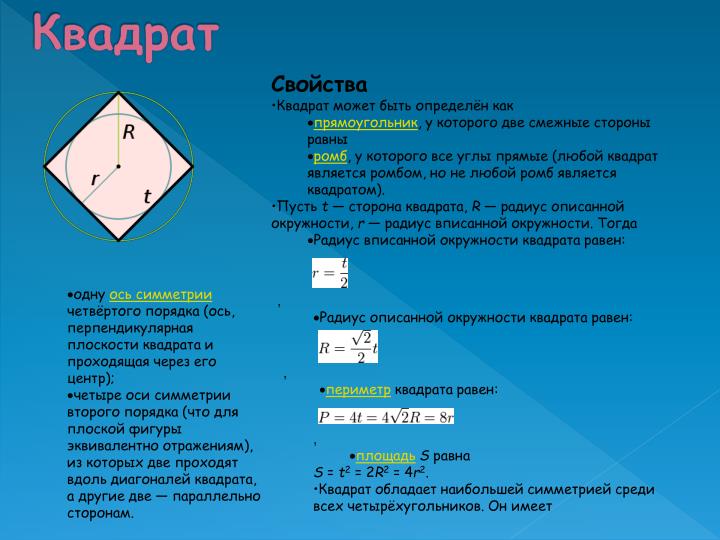
• одну ось симметрии четвёртого порядка (ось, перпендикулярная плоскости квадрата и проходящая через его центр);
• четыре оси симметрии второго порядка (что для плоской фигуры эквивалентно отражениям), из которых две проходят вдоль диагоналей квадрата, а другие две - параллельно сторонам.

• ,
  • Радиус описанной окружности квадрата равен:

• ,
  • периметр квадрата равен:

• ,
  • площадьS равна
• S = t2 = 2R2 = 4r2.
• Квадрат обладает наибольшей симметрией среди всех четырёхугольников. Он имеет

При изучении признаков равенства треугольников в курсе геометрии 7 класса возникли вопросы: Существуют ли признаки равенства четырёхугольников? Если да, то по скольким элементам? Можно ли их сформулировать и доказать, опираясь на признаки равенства треугольников?

Цель: Сформулировать и доказать признаки равенства четырёхугольников.

Задачи: 1) Изучить литературу по данной теме.

2) Исследовать все различные комбинации наборов сторон и углов из четырёх элементов и, либо доказать признак, либо опро- вергнуть его, приведя контрпример.

3) Исследовать все случаи различных комбинаций из 5 элементов, сформулировать и доказать признак, либо опровергнуть.

1)Определение 1.

Две геометрические фигуры называются равными, если их можно совместить наложением.

Определение 2.

Два четырехугольника называются равными, если их можно совместить наложением.

Гипотеза 1.

Существуют признаки равенства четырехугольников по четырем элементам.

Таблица №1

ПО ЧЕТЫРЁМ УГЛАМ

∠A=∠A1, ∠B=∠B1

ВЫВОД: ABCD!=A1B1CD

2)ПО ТРЁМ УГЛАМ И СТОРОНЕ а)

ВЫВОД:ABCD!=ABC1D1

∠C=∠C1, ∠B= ∠B1

ВЫВОД: ABCD!=AB1C1D_

3)ПО ДВУМ УГЛАМ И ДВУМ СТОРОНАМ а)

ВЫВОД: ABCD!=ABCD1

ВЫВОД: ABCD!=ABCD1

ВЫВОД: ABCD!=ABC1D1

ВЫВОД: ABCD!=ABCD1

ВЫВОД: ABCD!=AB1C1D

ВЫВОД: ABCD!=AB1C1D

4) ПО УГЛУ И ТРЁМ СТОРОНАМ а) BC=BC1

ВЫВОД: ABCD!=ABC1D

ВЫВОД: ABCD!=ABC1D1

5)ПО ЧЕТЫРЁМ СТОРОНАМ

BC=BC1, CD=CD1, AD=AD1

ВЫВОД: ABCD!=ABC1D1

(смотри Приложение №1 - с. 29)

ПРИЗНАКОВ РАВЕНСТВА ЧЕТЫРЁХУГОЛЬНИКОВ ПО ЧЕТЫРЁМ

ЭЛЕМЕНТАМ НЕ СУЩЕСТВУЕТ.

Гипотеза 2

Существуют признаки равенства четырёхугольников по пяти элементам.

Таблица№2

Признак 1

Если четыре стороны и угол одного четырёхугольника соответственно равны четырём сторонам и углу другого четырёхугольника, то такие четырёхугольники равны.

ABCD И ABCD- четырёхугольники. AB=AB, BC= BC, CD=CD,

DA=DA,∠A=∠A.

Доказать:

ABCD=ABCD

Доказательство:

Вывод: Т. к. соответственные стороны и соответственные углы четырёхугольников равны, то они совместятся наложением, а значит- по определению равных фигур - ABCD=ABCD.

Признак 2

Если три стороны и два угла между ними одного четырёхугольника соответственно равны трём сторонам и двум углам между ними другого четырёхугольника, то такие четырёхугольники равны.

Т. к. соответственные стороны и углы четырёхугольников равны, то они совместятся наложением, а значит- по определению равных

Фигур- ABCD=ABCD.

Если три стороны и два угла, не лежащие между ними, одного четырёхугольника соответственно равны трём сторонам и двум углам, не лежащим между ними, другого четырёхугольника, то такие четырёхугольники равны.

Примечание:

Случай, где углы четырёхугольника тупые доказывается аналогично, достаточно перейти к смежным, соответственно равным углам.

Признак 4

Если два противолежащих угла и три стороны одного четырёхугольника соответственно равны двум противолежащим углам и трём сторонам другого четырёхугольника, то такие четырёхугольники равны.

Вывод: ABCD!=AB1CD

Признак 5

Если три угла и две стороны между ними одного четырёхугольника соответственно равны трём углам и двум сторонам между ними другого четырёхугольника, то такие четырёхугольники равны.

Признак 6

Если три угла и две смежные стороны, не лежащие между ними, одного четырёхугольника, соответственно равны трём углам и двум сторонам, не лежащим между ними, другого четырёхугольника, то такие четырёхугольники равны.

Признак 7

Если три угла и две смежные стороны, одна из которых лежит между данными углами, одного четырёхугольника, соответственно равны трём углам и двум смежным сторонам, одна из которых лежит между двумя данными углами другого четырёхугольника, то такие четырёхугольники равны.

∠C=∠C1, ∠B=∠B1

Вывод: ABCD!=AB1C1D

По стороне и четырём углам

∠C=∠C1, ∠B=∠B1

Вывод: ABCD!=AD1C1D

Методика исследований

1) Эмпирические (изучение литературы, сбор сведений, сбор и обработка статистического материала)

2) Теоретические (сравнение и обобщение данных, составление таблиц)

3) Практические (построения с помощью циркуля и линейки, доказательства).

Этапы исследований

1) Изучение и исследование материала по теме.

2) Изучение проблемы.

3) Обработка материала и выработка практических рекомендаций.

Результаты исследований

1) Рассмотрев все различные наборы из четырёх элементов (сторон и углов) четырёхугольника, получили 12 случаев, к каждому из них с помощью циркуля и линейки привели контрпример, построив 2 неравных четырёхугольника по данным элементам.

2) Рассмотрев все различные наборы из 5 элементов четырёхугольника, получили 10 случаев, 7 из которых стали признаками равенства четырёхугольников, а к 3 случаям привели контрпример, построив неравные между собой четырёхугольники.

При изучении данной темы было установлено: существуют признаки равенства четырёхугольников по 5 элементам.

1. По 4 сторонам и углу: если четыре стороны и угол одного четырёхугольника соответственно равны четырем сторонам и углу другого четырёхугольника, то такие четырёхугольники равны.

2. По 3 сторонам и 2 углам между ними: если три стороны и два угла между ними одного четырёхугольника соответственно равны трем сторонам и двум углам между ними другого четырёхугольника, то такие четырёхугольники равны.

3. По 3 сторонам и 2 углам, не лежащим между ними: если три стороны и два угла, не лежащие между ними, одного четырёхугольника соответственно равны трем сторонам и двум углам, не лежащим между ними, другого четырёхугольника, то такие четырёхугольники равны.

4. По 2 противолежащим углам и 3 сторонам: если два противолежащих угла и три стороны одного четырёхугольника соответственно равны двум противолежащим углам и трем сторонам другого четырёхугольника, то такие четырёхугольники равны.

5. По 3 углам и 2 сторонам между ними: если три угла и две стороны между ними одного четырёхугольника соответственно равны трем углам и двум сторонам между ними другого четырёхугольника, то такие четырёхугольники равны.

6. По 3 углам и 2 смежным сторонам, не лежащим между ними: если три угла и две смежные стороны, не лежащие между ними, одного четырёхугольника соответственно равны трем углам и двум смежным сторонам, не лежащим между ними, другого четырёхугольника, то такие четырёхугольники равны.

7. По 3 углам и 2 смежным сторонам, одна из которых лежит между данными углами: если три угла и две смежные стороны, одна из которых лежит между данными углами, одного четырёхугольника соответственно равны трем углам и двум смежным сторонам, одна из которых лежит между данными углами другого четырёхугольника, то такие четырёхугольники равны.

Заключение

Была проделана работа по доказательству признаков равенства четырёхугольников. Для доказательства были использованы признаки равенства треугольников, определение равных фигур, геометрические построения с помощью циркуля и линейки.

В результате работы сформулировали и доказали 7 признаков по пяти элементам. Эти признаки могут быть полезны для тех, кто начинает изучать геометрию, учится сам формулировать и доказывать теоремы, а также в практической деятельности человека, например, при нахождении площадей.