Образовательный портал. Образование / Среднее образование и школа / Как найти периметр фигуры с вырезом внутри. Умение применять знания в нахождении периметра и площади геометрических фигур. равные фигуры имеют одинаковую площадь

Как найти периметр фигуры с вырезом внутри. Умение применять знания в нахождении периметра и площади геометрических фигур. равные фигуры имеют одинаковую площадь

08.09.2019

Слово «изопериметрический» происходит от слов «изос» (по-гречески «равный») и «периметр». Изопериметрическая задача (на плоскости) состоит в нахождении фигуры, имеющей наибольшую площадь среди всех фигур с одним и тем же периметром. Решение изопериметрической задачи является также решением и другой задачи, а именно: найти фигуру наименьшего периметра среди всех равновеликих фигур.

Площадь - это площадь поверхности двумерных форм. Он измеряется в квадратных единицах. Периметр - это общее расстояние вокруг внешней части двумерной формы. Вы вычисляете его, добавляя вместе все длины фигуры. Сопоставьте слово со словами, которые вы знаете.

Фигуры, имеющие разные площади, не могут быть равны

Игровая площадка - это место, где вы играете, поэтому площадь - это пространство в форме. Область на футбольном поле, где вратарь может забрать мяч. Область находится внутри этого прямоугольника, поэтому область представляет собой пространство в форме.

В самом деле, пусть среди фигур, имеющих периметр наибольшая площадь – у фигуры и эта площадь равна Рассмотрим произвольную другую фигуру той же площади. Пусть ее периметр равен Рассмотрим подобную ей фигуру с периметром Площади фигур и относятся так же, как квадраты периметров, то есть как к , поэтому площадь фигуры равна Поскольку ее периметр, по предположению, равен ее площадь меньше, чем у фигуры то есть меньше А значит, откуда Получается, что фигура имеет меньший периметр, чем любая другая равновеликая ей фигура.

Мы поем песню, когда мы ходим по краям столов в нашей комнате. Речь идет о песне «Здесь мы идем вокруг тутового туши». Здесь мы обойдем ограду по периметру, ограду периметра, ограду периметра. Здесь мы обойдем ограду по периметру, сложите все стороны.

Второй способ запомнить разницу

Сделайте повторение или песню, чтобы запомнить различия. Вы считаете квадраты или умножаете. Умножьте длину раз ширины. Хороший простой способ - запомнить эти.

Еще один отличный способ, хотя и повальный, как запомнить разницу в площади и периметре

Составная форма - это форма, которая имеет неправильное расположение сторон или углов и должна быть разбита на более простые фигуры, прежде чем вы сможете выработать область или периметр.

Вообще, поскольку у подобных фигур площади пропорциональны квадратам периметров, у всех них одинакова величина S /p 2 , а у фигур разной формы эта величина может отличаться. У фигур, представляющих решение изопериметрической задачи (независимо от размера), величина S /p 2 должна быть наибольшей.
(В дальнейшем будем называть эту величину изопериметрическим частным ).

Итак, как вы разрабатываете область сложной формы выше?

Это полезный способ взглянуть на формы, которые нелегко решать. Помните, что это пространство внутри. Мы знаем, что для выработки прямоугольника путем умножения длины по ширине. Поэтому, когда дело доходит до составных фигур, если мы разделим форму на прямоугольники, тогда станет намного легче найти область общей формы.

Пример 1 показывает некоторые методы для разработки области сложной формы

Выше мы видим, что если мы разделим составную форму на два прямоугольника, площадь будет одинаковой. Таким образом, мы находим область обоих прямоугольников, а затем добавляем их. Лучше нарисовать эти строки, чтобы вы могли точно видеть, что вам нужно для разработки. Добавьте эти отдельные области для каждого прямоугольника вместе, чтобы найти общую площадь составной формы.

Разделите составную форму на ряд прямоугольников.
Разработайте недостающие длины, которые вам нужны по краю.
Разработайте область каждого отдельного прямоугольника.

Первый и второй способ состоит в том, чтобы разбить составную форму на два прямоугольника.

Заметим, что задача о наименьшей площади фигур с одним и тем же периметром особого смысла не имеет: например, при данном периметре p можно делать все меньше и меньше одну из сторон прямоугольника (a ), другая же его сторона, равная (p /2 – a ), ограничена сверху величиной p /2, а значит, площадь этой фигуры будет не больше ap /2. Даже если, например, p = 1 000 000 км, можно сделать площадь S < 0, 000 001 мм 2 , если положить a = 2∙10 –8 мм; если надо получить еще в 1000 раз меньшую площадь, надо и a уменьшить в 1000 раз, и т. д. Таким образом, минимальной площади при данном периоде не существует: площадь может сколь угодно мало отличаться от нуля.

Это делается по-разному с обоими примерами, но основные математики одинаковы. Вы обрабатываете область каждого прямоугольника, а затем добавляете их вместе. Последний метод разработки области для этой составной формы немного отличается. Вместо того, чтобы добавить область двух прямоугольников вверх, как в предыдущих примерах, вы можете сделать что-то совсем другое.

Используйте метод, который вы можете «видеть» лучше

Разработайте область большой формы вокруг сложной формы.
Это представлено зелеными линиями на примере.
Затем вам нужно выработать область формы, которая вырезана.

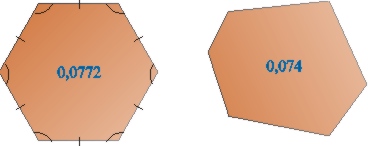
Если вы можете увидеть, как разделить сложную форму на два или более прямоугольника проще, чем определить способ вырезания, следуйте этому правилу.

По аналогии с указанной изопериметрической задачей на плоскости можно рассмотреть и пространственную изопериметрическую задачу: какое трехмерное тело среди всех тел той же площади поверхности имеет наибольший объем. Уже древнегреческим математикам был известен ответ в изопериметрической задаче: в плоском случае искомая фигура – это круг (а в пространственном – шар). На эту мысль, наводит, во-первых, непосредственное сравнение площадей некоторых фигур равного периметра (или равной площади поверхности). Посмотрите на зависимость изопериметрического частного от формы плоских фигур.

Форма - это объект, имеющий определенный тип подвижных ручек и числовые параметры, позволяющие модифицировать эту форму, сохраняя ее тип. Например, со звездой вы можете изменить количество вершин, их длину, угол, округление и т.д. - но звезда остается звездой. Таким образом, форма «менее свободна», чем путь, но часто более удобна и интересна. Вы можете преобразовать форму в путь, но обратное преобразование невозможно.

Прямоугольники, имеющие одинаковую площадь

Форма создается на холсте кликом и перетаскивается с помощью соответствующего инструмента. После создания формы он отображает свои ручки, поэтому вы всегда можете изменить его, перемещая эти ручки. Когда вы перемещаете курсор мыши над дескриптором, в строке состояния отображаются сообщения, сообщающие вам что вы можете сделать, щелкнув по нему или перемещая его в комбинации с различными ярлыками. Кроме того, каждый инструмент формы отображает свои параметры в панели управления инструментом. Обычно он имеет несколько числовых полей и кнопку для сброса этих полей.

Во-вторых, некоторые физические соображения также показывают, что ответ в изопериметрической задаче – это круг или шар. Например, капельки воды и мыльные пузыри не случайно имеют форму шара: силы поверхностного натяжения действуют так, чтобы уменьшать площадь поверхности. Характерно также, что кошки, когда холодно, спят, максимально сворачиваясь в клубок: так они уменьшают площадь поверхности тела, поскольку, чем меньше поверхность, тем меньше тепла они расходуют во внешнее пространство.

Когда выбрана одна или несколько форм используемого инструмента, изменение значений этих полей панели управления позволяет вам изменять выбранную форму (формы). Все изменения, внесенные в панель управления, сохраняются для применения к следующей фигуре, которую вы рисуете с помощью этого инструмента. Например, после изменения количества вершин звезды звезды, которые вы создадите позже будет иметь такое же количество вершин. Более того, простой факт выбора данной формы посылает свои параметры на панель управления инструмента и, таким образом, позволяет определить значения для форм этого типа, которые вы создадите позже.

В третьих, древние греки считали круг наиболее совершенной фигурой (она максимально симметрична, именно такую форму имеют небесные тела и их орбиты). Это соображение увеличивало их уверенность в том, что именно круг, помимо других своих интересных свойств, должен также быть решением изопериметрической задачи.

Но вот геометрически древние греки доказать этого не могли, хотя и пришли к ряду частных, но важных результатов на эту тему, в том числе, в решении разнообразных задач о том, у какой фигуры определенного типа с заданными условиями площадь имеет наибольшее значение. Исследования такого рода имели не только теоретическое, но и практическое значение: при разделе земли в древности иногда совершались махинации, связанные с выдачей кусков большого периметра и маленькой площади; периметр легче измерить, чем площадь, поэтому некоторые доверчивые клиенты судили о величине участка земли по периметру.

Равные фигуры имеют одинаковую площадь

Когда вы используете инструмент фигуры, вы можете выбрать объект, щелкнув его. Прямоугольник является самым простым, но, вероятно, наиболее распространенным видом дизайна и иллюстрации. Создайте новый прямоугольник рядом с ним. Ярлыки для рисования прямоугольников.

Как вы можете видеть, выбранный прямоугольник отображает три ручки в трех своих углах. На самом деле, есть четыре ручки, но два из них перекрываются, если прямоугольник не закруглен. Эти два являются закругленными ручками, а два других - ручками изменения размера.

Наверное, один из самых простых результатов на тему изопериметрических фигур – теорема о том, что из всех прямоугольников одинакового периметра наибольшую площадь имеет квадрат. В самом деле, пусть периметр всех рассматриваемых прямоугольников равен 4 a , а у данного прямоугольника две большие стороны равны (a + x ) каждая, а две меньшие, соответственно, (a – x ) каждая. Тогда площадь прямоугольника равна (a + x ) (a – x ) = a 2 – x 2 , то есть она не меньше a 2 и достигает своего наибольшего значения тогда, когда прямоугольник является квадратом со стороной a .

Посмотрим сначала на скругленные ручки. Введите один из них и перетащите его. Четыре угла прямоугольника округляются, и теперь вы можете увидеть вторую ручку округления, которая всегда находится в одном и том же месте в углу. Если вам нужны круговые закругленные углы, вам нечего делать. Если вы хотите округлить с другим радиусом в зависимости от стороны, вы можете переместить второй дескриптор влево.

Здесь первые два прямоугольника имеют круговые закругленные углы, а два других имеют закругленные углы эллиптически. Всегда с помощью инструмента «Прямоугольник» щелкните по этим прямоугольникам, чтобы выбрать их и наблюдать за их закругленными ручками.

В «Началах» Евклида имеется единственная задача на максимум площади. Требуется в данный треугольник ABC вписать параллелограмм ADEF наибольшей площади. Попробуйте экспериментальным путем найти искомый параллелограмм.

Ответ в этой задаче таков: параллелограмм имеет наибольшую площадь, когда точка D делит сторону BC пополам. Евклид доказывает этот результат с помощью подобия треугольников. На первый взгляд кажется, что данная задача не имеет большого отношения к изопериметрическим задачам: в самом деле, периметры рассматриваемых параллелограммов не равны друг другу. Тем не менее, если «сдвинуть» вершину B параллельно стороне AC , то площади параллелограмма ADFE и треугольников ABC , DEB и FEC не изменятся (потому что не изменятся их высоты и основания). Задача при этом сводится к такой: в данный прямоугольный треугольник вписать прямоугольник наибольшей площади.

Часто радиус и форма закругленных углов должны иметь одинаковые пропорции внутри композиции, даже если размеры прямоугольников различны. в панели управления этого инструмента есть группа из четырех кнопок, вторая - две концентрические закругленные углы. Эта кнопка позволяет вам определить, следует ли масштабировать радиусы округлых углов или нет, когда вы изменяете размер прямоугольника.

Здесь, например, дублированный оригинальный красный прямоугольник и его размеры изменялись несколько раз в соответствии с разными пропорциями, кнопка «сохранить масштаб округлений» деактивирована. Обратите внимание, что размер и форма закругленных углов остаются одинаковыми для всех прямоугольников, так что закругленные углы накладываются точно в верхнем правом углу рисунка. Все синие пунктирные прямоугольники были получены после изменения размера оригинала в селекторе без корректировки закругленных ручек.

Далее: если пропорционально сжать или растянуть этот прямоугольный треугольник вдоль одного из катетов так, чтобы катеты стали равны, то высоты данных прямоугольника и треугольников изменятся в одном и том же отношении, а задача примет следующий вид: в данный прямоугольный равнобедренный треугольник вписать прямоугольник наибольшей площади.

Чтобы сравнить, вот тот же состав, но на этот раз создал кнопку «сохранить масштаб округления». Теперь все прямоугольники имеют по-разному закругленные углы, и в верхнем правом порядке нет суперпозиции. Этот результат такой же, как тот, который вы бы получили, преобразовывая исходный прямоугольник в путь и затем изменяя размеры этого прямоугольника. путь.

Вот ярлыки для манипулирования закругленными ручками прямоугольника. Важным преимуществом этих элементов управления является то, что они могут влиять на несколько прямоугольников одновременно. Если выбраны объекты, отличные от прямоугольников, они будут игнорироваться - будут изменены только прямоугольники. Теперь давайте посмотрим на ручки прямоугольника. Возможно, вам интересно, что это такое, потому что вы можете изменить размер прямоугольника с помощью селектора?

Это задача вполне изопериметрическая: нетрудно видеть, что все рассматриваемые прямоугольники имеют один и тот же периметр – насколько увеличивается одна сторона, настолько уменьшается другая. Но решение изопериметрической задачи для прямоугольников мы уже знаем, это квадрат, а его вершина делит гипотенузу равнобедренного прямоугольного треугольника пополам. Значит, и в исходной задаче вершина искомого параллелограмма делит соответствующую сторону треугольника пополам.

Проблема с селектором заключается в том, что для него понятия горизонтальной и вертикальной относятся к странице. Поскольку есть два ручка изменения размера, вы можете изменить размеры прямоугольника в любом направлении и даже параллельно его сторонам. Изменение размеров сохраняет округлые радиусы углов.

Вот ярлыки для манипулирования ручками прямоугольника. Вот несколько дополнительных примеров композиций с прямоугольниками, включая закругленные углы и фоновые градиенты. Инструмент «Эллипс» позволяет создавать эллипсы и круги, которые вы можете преобразовать в круговые диаграммы или дуги.

Зенодор (II в. до н. э.) написал целый трактат «Об изопериметрических фигурах». Хотя трактат Зенодора не сохранился, некоторые его результаты дошли до нас в изложении математиков Паппа (III в. н. э.) и Теона (IV в. н. э.), в том числе следующие теоремы:

Таким образом, чем «ближе» многоугольник к кругу, тем, действительно, больше его изопериметрическое частное.

Давайте посмотрим на ручки эллипса. Выберите следующий эллипс. Еще раз, сначала вы видите только три ручки, но есть четыре ручки, а справа есть две ручки, которые перекрываются и «открывают» эллипс. первая из этих ручек, вторая становится видимой, перемещение этих ручек позволяет вам получить все виды арки или круговые диаграммы.

Чтобы получить круговую диаграмму, переместите дескриптор на внешнюю сторону эллипса; чтобы получить дугу, переместите ее внутрь, над вами можно увидеть 4 каменщика слева и 3 дуги вправо. Обратите внимание, что дуги - это открытые формы, то есть короткий контур вдоль эллипса, но не соединяет концы дуги. Это становится очевидным, если вы удаляете фон, сохраняя только видимый контур.

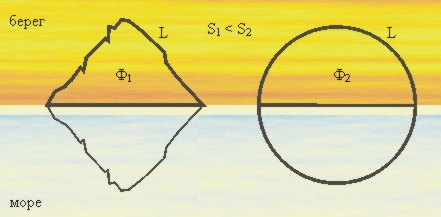
Нельзя не упомянуть об очень древней задаче, известной как задача Дидоны. Согласно древнему мифу, воспроизведенному в поэме Вергилия «Энеида», будущая основательница Карфагена – Дидона (вероятно, IX в. до н. э.) – бежала от преследований своего брата, тирана финикийского города Тир, на корабле с небольшим отрядом преданных ей людей. Они высадились на североафриканском побережье, принесли богатые подарки местному царю и попросили о выделении им участка; царь согласился отдать лишь «столько земли, сколько занимает воловья шкура». Тогда Дидона сделала из шкуры длинный тонкий ремень и огородила им значительную территорию на берегу моря, где и возник город Карфаген. Задачей Дидоны традиционно называется задача о том, какую форму должен иметь этот участок, чтобы занять наибольшую территорию при заданной длине ремня. Рассмотрим эту задачу для случая, когда берег прямолинеен. Пусть ремень имеет длину L и опоясывает некую фигуру Ф 1 . Отразим ее относительно берега. Тогда ремень и его отражение вместе являются границей (длины 2 L ) новой фигуры Ф 2 , составленной из фигуры Ф 1 и ее отражения. Если решение изопериметрической задачи – круг, то площадь Ф 2 (при данном периметре 2 L ) максимальна, когда Ф 2 – круг. Но поскольку площадь Ф 2 ровно в 2 раза больше, чем у Ф 1 , площадь Ф 1 тоже максимальна, если Ф 2 – круг, а ремень, соответственно, образует полуокружность.

Смотрите ледяную круговую диаграмму. Другие два дескриптора эллипса используются для изменения его размера вокруг центра. Связанные с ним сочетания похожи на сочетания клавиш округления прямоугольника. И, подобно ручкам прямоугольника, эти ручки позволяют регулировать ширину и высоту эллипса в собственной системе координат, что означает, что эллипс, который был повернут или наклонен, может легко быть отрегулированным параллельно его осям. Попробуйте изменить размеры этих эллипсов, используя их ручки изменения размера.

Звезды - самые сложные и интересные формы. Это особенно весело - почти захватывающий! Инструмент «Звезда» позволяет создавать два типа похожих фигур: звезды и полигоны. Звезда имеет две ручки, позиции которых определяют длину и форму ее ветвей, многоугольник имеет только ручку, которая позволяет перемещение для изменения размера и поворота этого многоугольника.

Рис. 7. Задача Дидоны

194. Запишите выражения для площадей и периметров фигур, изображённых на рисунке 38. Постарайтесь найти разные способы.

195.Объясните, почему площадь каждой из закрашенных фигур равна 1 см2 (рис. 39).

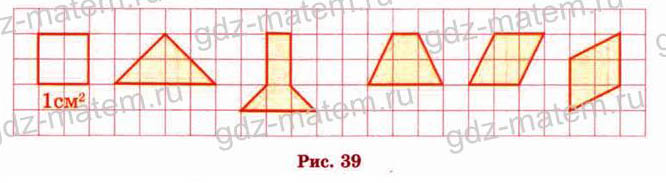
Потому что каждую из фигур можно разрезать так, чтобы потом из получившихся частей сложить единичный квадрат.

196.Рассмотрите рисунок 40, выполните задания и ответьте на вопросы.

1)Найдите:

.равные прямоугольники;

.прямоугольники, имеющие одинаковую площадь;

.прямоугольники, имеющие одинаковый периметр.

2)Подумайте, можно ли утверждать, что:

.если прямоугольники имеют одинаковую площадь, то они равны;

.если прямоугольники имеют одинаковый периметр, то они равны;

.если два прямоугольника имеют одинаковую площадь, то их периметры равны;

.если один из двух прямоугольников имеет большую площадь, то он имеет и больший периметр;

Если площадь одного прямоугольника меньше площади другого, то первый прямоугольник можно полностью расположить внутри второго.

197.1) Сравните площади фигур, изображённых на рисунке 41. Есть ли среди изображённых фигур равные? Ответы обоснуйте.

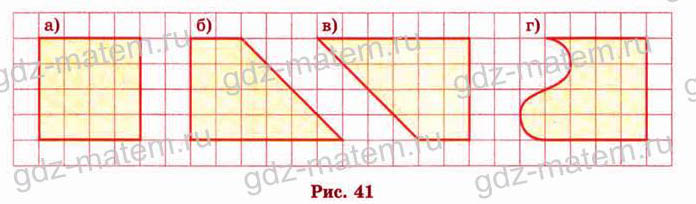
2)Подумайте, какие из следующих утверждений (высказываний) истинны, а какие — ложны:

.равные фигуры имеют одинаковую площадь;

.фигуры, имеющие одинаковую площадь, равны;

.если фигуры не равны, то их площади тоже не равны;

.фигуры, имеющие разные площади, не могут быть равны.

3)На листе бумаги в клетку изобразите две равные фигуры и две имеющие одинаковую площадь неравные фигуры.

198.Догадайтесь, какова сторона квадрата, площадь которого равна:

а)25 см 2 ; б) 64 см 2 ; в) 100 см 2 ; г) 144 см 2 .

а) 5 см; б) 8 см; в) 10 см;г) 12 см.

199.Каким может быть периметр прямоугольника площадью 100 см2? Подумайте, какой из всех прямоугольников с такой площадью имеет наименьший периметр?

Периметр такого прямоугольника больше или равен 40 см и может быть сколь угодно большим. Наименьший периметр имеет квадрат со стороной 10, его периметр равен 40.

Материалы по теме:

Карта сайта