Как найти отношение сторон трапеции. Трапеция, средняя линия трапеции, треугольник

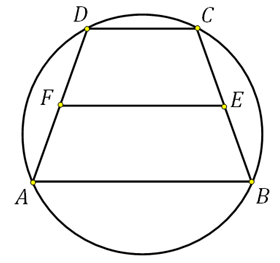
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.

Какую теорию необходимо помнить? Это:

Задачи с трапециями, которые имеются на блоге можно посмотреть здесь .

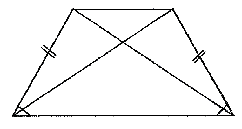
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:

Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.

27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 0 , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?

Посмотрите: равнобедренная трапеция с углом при основании равным 60 0 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:

В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее

То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.

*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 180 0 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.

27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:

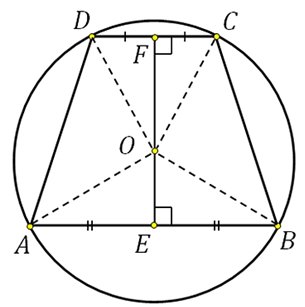
Отрезок EF является высотой трапеции, его нам нужно найти.

В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:

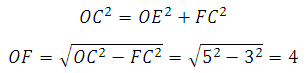
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:

Таким образом EF=FO+OE=4+3=7.

Теперь важный нюанс!

В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.

А если бы в условии не было дано эскиза?

Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями.

Четырёхугольник, у которого только две стороны параллельны называются трапецией .

Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.

Средняя Линия Трапеции

Средняя линия - это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.

Теорема:

Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.

Теорема:

Длина средней линии равна среднему арифметическому длин её оснований

MN || AB || DC
AM = MD; BN = NC

MN средняя линия, AB и CD - основания, AD и BC - боковые стороны

MN = (AB + DC)/2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин её оснований.

Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.

Средняя Линия Треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.

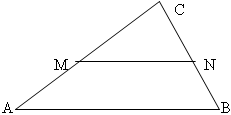
AM = MC and BN = NC =>

Применение свойств средней линии треугольника и трапеции

Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.

Трапеция — это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.

Также встречаются такие названия, как равнобокая или равнобочная .

— это трапеция, у которой углы при боковой стороне прямые.

Элементы трапеции

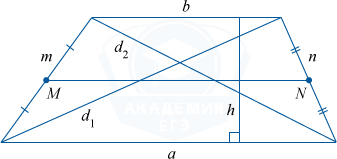
a, b — основания трапеции (a параллельно b ),

m, n — боковые стороны трапеции,

d 1 , d 2 — диагонали трапеции,

h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),

MN — средняя линия (отрезок, соединяющий середины боковых сторон).

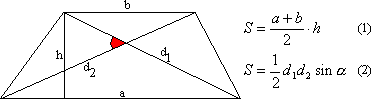
Площадь трапеции

1. Через полусумму оснований a, b и высоту h : S = \frac{a + b}{2}\cdot h
2. Через среднюю линию MN и высоту h : S = MN\cdot h
3. Через диагонали d 1 , d 2 и угол (\sin \varphi ) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}

Свойства трапеции

Средняя линия трапеции

Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:

MN || a, MN || b, MN = \frac{a + b}{2}

Сумма углов трапеции

Сумма углов трапеции , прилежащих к каждой боковой стороне, равна 180^{\circ} :

\alpha + \beta = 180^{\circ}

\gamma + \delta =180^{\circ}

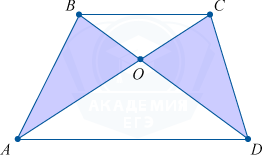
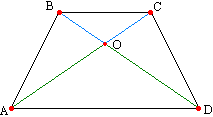
Равновеликие треугольники трапеции

Равновеликими , то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC , образованные боковыми сторонами.

Подобие образованных треугольников трапеции

Подобными треугольниками являются AOD и COB , которые образованы своими основаниями и отрезками диагоналей.

\triangle AOD \sim \triangle COB

Коэффициент подобия k находится по формуле:

k = \frac{AD}{BC}

Причем отношение площадей этих треугольников равно k^{2} .

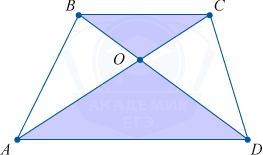
Отношение длин отрезков и оснований

Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:

\frac{OX}{OY} = \frac{BC}{AD}

Это будет являться справедливым и для высоты с самими диагоналями.

Описанная около трапеции окружность

Каждая равнобокая трапеция может содержать описанную окружность . Только равнобокую трапецию возможно вписать в окружность.

Вписанная в трапецию окружность

Треугольники AOB и DOC являются прямоугольными, если трапеция ABCD описана около окружности. Центром же вписанной окружности будет являться точка O .

Опущенные на гипотенузы, высоты этих треугольников, тождественны радиусу вписанной окружности, а высота трапеции тождественна диаметру вписанной окружности.

Раздел 2. Четырехугольники

I . Справочные материалы.

1. Трапеция, ее виды и свойства

Свойства трапеции, которые часто используются при решении задач:

1) Диагонали трапеции разбивают её на четыре треугольника с общей вершиной. Площади треугольников, прилежащие к боковым сторонам, равны.

2) В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которой лежат боковые стороны, лежат на одной прямой (точки М, N, О и К).

3) В равнобокой трапеции углы при основании равны.

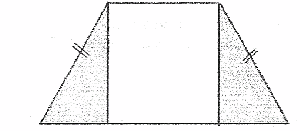
4) В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции,

5) В равнобокой трапеции диагонали равны.

6) В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой их полусумме.

7) Во всякой трапеции серединам боковых сторон и середины диагоналей лежат на одной прямой.

8) Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.

9) во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований.

10) Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

11) Трапецию можно описать около окружности тогда и только тогда, когда сумма оснований равна сумме боковых сторон.

2.Вписанные и o писанные четырёхугольники.

1)Если четырёхугольник вписан в окружность, то сумма противолежащих углов равна 180°.

Верно и обратное: если сумма противолежащих углов четырёхугольника равна 180°, то около этого четырёхугольника можно описать окружность.

2)Около параллелограмма можно описать окружность тогда и только тогда, когда этот параллелограмм есть прямоугольник.

3)Около трапеции можно описать окружность, если она равнобокая.

четырёхугольник называется описанным около окружности, если окружность касается всех его сторон.

4)Если четырёхугольник описан около окружности, то суммы противолежащих сторон равны.

5)Если в выпуклом четырёхугольнике суммы противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

3. Площади четырёхугольников.

Площадь выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними.

Ромб

1. Диагонали ромба взаимно перпендикулярны и делят углы пополам.

2. Площадь определяется формулами:

Параллелограмм

1. Сумма квадратов диагоналей равна сумме квадратов всех его сторон.

2. Площадь определяется формулой

II . Дополнительные материалы

1)Свойства вписанного выпуклого четырехугольника .

а)В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым

б)Обратно: если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым, то около него можно описать окружность

Доказательство.

а) Пусть АВСD есть вписанный выпуклый четырехугольник; требуется доказать„ что

Так как сумма всех четырех углов сякого выпуклого четырехугольника равна 4d, то достаточно доказать только одно из требуемых равенств.

докажем, например, что

Углы В и D как вписанные, измеряются: первый-половиной дуги ADC, второй- половиной дуги АВС;

Следовательно, сумма

б) Пусть АВСD есть такой выпуклый четырехугольник, у которого

Через какие-нибудь три его вершины, например, через A,В и С, проведем окружность (что всегда можно сделать).

Четвертая вершина D должна находиться на этой окружности, пoтoму что в противном случае вершина угла В лежала бы или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги АВС; поэтому cyммa измерялась бы полусуммой дуг ADC и АВС и, значит, сумма Следствия

1) из всех параллелограммов только вокруг прямоугольника можно описать окружность.

2) около трапеции можно описать окружность только тогда, когда она равнобокая.

2) Свойство описанного четырехугольника. В описанном четырехугольнике суммы противоположных сторон равны.

Пусть АВСD будет описанный четырехугольник, Т.е, стороны его касаются окружности; требуется доказать, что АВ+СВ=ВС+АD

Обозначим точки касания буквами M, N, Р и Q. Так как две касательные, проведенные из одной точки окружности, равны, то АМ.=АQ, ВМ=ВN, CN=СР, DP=DQ.

Следовательно, АМ+МВ+СР+РD=AQ+QD+BN+NC. Т.е. АВ+СD=АD+ВС.

III . Вводные задачи.

Задача 1.

Средняя линия трапеции ABCD равна 15. AD – большее основание трапеции, A = 90°, D = 60°, BAC = 30°. Найдите длину стороны CD .

В ∆ABC (он прямоугольный) BC = – по свойству катета, лежащего против угла в 30°.

BAC = 30°, значит, CAD = 90° – 30° =
= 60°, следовательно, ∆ACD равносторонний,
т. е. AC = CD = AD = 2BC .

Средняя линия MN = 3BC = 30,

BC = 10, значит, CD = 2 · 10 = 20.

Ответ: 20.

Задача 2 .

Сторона AB параллелограмма ABCD равна а его диагонали равны 20 и 24. Найдите сторону BC .

Д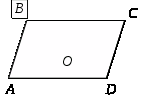ля любого выпуклого четырехугольника справедливо

где a , b , c и d – стороны четырехугольника, а d 1 , d 2 – его диагонали.

В параллелограмме

20 2 + 24 2 = 2(() 2 + b 2), b > 0; b 2 + 88 = 488,b 2 = 400, b = 20.

Задача 3 .

Основания трапеции равны 4 и 10, а ее боковые стороны – и 15. Найдите косинус наименьшего угла этой трапеции.

1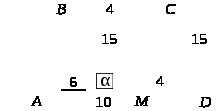) Проведем BM ∥ CD , значит, BMA =D , ВСDМ – параллелограмм, так как ВМ || MD , ВМ || СD . Следовательно, ВС = MD = 4,
BM = CD = 15, AM = AD – MD = 10 – 4 = 6.

2) В ∆AMB против большей стороны (выбирая из AB и BM ) лежит больший угол: AB BM, значит, BMA A .

Ответ: 0,8.

Задача 4.

Определите периметр равнобокой трапеции, у которой длина меньшего основания равна 7, диагонали перпендикулярны боковым сторонам и равны .

1) Проведем в трапеции ABCD высоту CF ,
тогда

∆ACD ∼ ∆AFC ,

2) Пусть FD = x , тогда AF = 7 + x

() 2 = (x + 7) (7 + 2x ),

36 · 2 = 49 + 21x + 2x 2 ,

2x 2 + 21x – 23 = 0,

D = 21 2 + 4 · 2 · 23 = 625,

х 1,2 =

3) Итак, AD = 7 +2 = 9;

P = 9 + 7 + 2 · 3 = 22.

Ответ: 22.

Задача 5.

В ромбе высота, проведенная из вершины тупого угла, делит сторону ромба пополам. Найдите периметр и высоту ромба, если меньшая диагональ его равна 7

1) В треугольнике ABD BK – высота и медиана, значит, ∆ABD -равнобедренный с основанием AD , т. е. AB = BD = 7 см. Тогда ∆ABD -равносторонний, значит, A = ABD = BDA = 60°.

2) P = 4AB = 4 · 7 = 28 (см).

3) BKD – прямоугольный, BK = AD sin BDK .

BK = 7 · sin 60° = (см). Ответ: 28 см; 3,5 см.

Задача 6.

Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD . Длина диагонали AC равна 12, длина боковой стороны BC равна 5. Найдите площадь трапеции.

1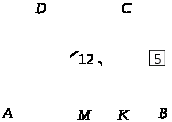) По условию AB = 2AD = 2DC .

Пусть M – середина AB , тогда AM = MB = CM ,
т. е. CM – медиана треугольника ABC и CM = AB , значит, ∆ABC прямоугольный с гипотенузой AB .Вершина C параллелограмма ABCD соединена с точкой N на стороне AB. Отрезок CN пересекает диагональ BD в точке P. Площадь треугольника BNP равна 8, а площадь треугольника BCP равна 12. Найдите площадь параллелограмма ABCD.

1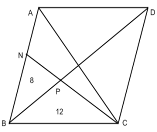) Треугольники BNP и BPC имеют общую высоту BH=>

SBNP/SBPC=PN/PC=>PN/NC=2/3;

2) Треугольники BPN и DPC подобны по

двум углам => SBPN/SDPC=(PN/PC) 2

SDPC=9/4; SBPN = (9/4)·8=18;

3) SBCD=SBPC+SDPC=12+18=30;

4) SABCD=2·SBCD=60; Ответ: 60

На стороне AB параллелограмма ABCD, как на диаметре, построена окружность, проходящая через точку пересечения диагоналей и середину стороны AD. Найдите углы параллелограмма.

Р

ешение:

1) По условию, AB – диагональ=> ABCD – ромб

P – середина АВ: по условию Q – середина AD=>PQ – средняя линия ∆ABD=BD=2PQ;PQ=R=>BD=2R;

PO=R – средняя линия ∆АBD=>AD=2·PO=R

∆ABD – правильный =>

Ответ: 60 o и 120 o .

Угол между сторонами АВ и СD четырехугольника ABCD=φ. Докажите, что AD 2 =AB 2 +BC 2 +CD 2 -2(AB·BCcosB + BC·CDcosC+CD·ABcosφ)

П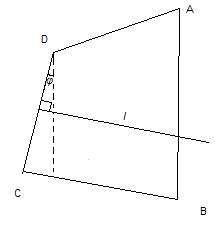о теореме косинусов AD 2 =AC 2 +CD 2 -2AC·CD·cosACD и AC 2 =AB 2 +BC 2 -2AB·BCcosB. A так как длина проекции отрезка АС на прямую l , перпендикулярную CD, равна сумме длин проекций отрезков АВ и ВС на прямую l, то ACcosACD=ABcosφ+BCcosC

V .Задачи для самостоятельного решения

№1. Докажите, что если ABCD прямоугольник, а Р- произвольная точка, то

АР 2 +СР 2 =DP 2 +BP 2

№2. Перпендикуляр, опущенный из вершины параллелограмма на диагональ, делит ее на отрезки длиной 6 и 15. Найдите большую сторону параллелограмма, если известно, что разность сторон равна 7.

№3. Одно из оснований трапеции равно 24, а расстояние между серединами диагоналей 4. найдите другое основание.

№4. Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты равна 17. Найдите радиус окружности, описанной около трапеции, если средняя линия равна высоте.

№5. В трапеции ABCD диагональ АС перпендикулярна боковой стороне СD. Окружность, описанная возле треугольника АВС, касается прямой CD, пересекает основание AD в точке М. Найдите площадь трапеции АBCD, если АМ=8, СМ=4.

№6. Окружность, центр которой лежит внутри квадрата PQRS, касается стороны PQ в точке К, пересекает сторону PS в точках А и В, а диагональ PR в точках С и D. Найдите радиус окружности, если АВ=16, СD=2√92

№7. В параллелограмме ABCD угол АВС=3п/4. окружность, описанная возле треугольника АВD, касается прямой CD. Найдите площадь параллелограмма, если диагональ BD=2

№8. Вершина С параллелограмма ABCD соединена с точкой N на стороне АВ. Отрезок CN пересекает диагональ BD в точке Р. Площадь треугольника BNP равна 8, а S ВСР =12. Найдите площадь параллелограмма АВСD.

№9. Найдите площадь трапеции, основания которой 6 и 26, а боковые стороны – 12 и 16.

Ответ: 153,6

№10. На стороне АВ параллелограмма АВСD как на диаметре построена окружность, проходящая через точку пересечения диагоналей и середину стороны АD. Найдите углы параллелограмма.

Ответ: 60,120,60,120.

VI . Контрольные задачи.

Вариант № 1.

1) В равнобедренную трапецию, площадь которой равна 80, вписана окружность радиуса 4. Найдите периметр трапеции.

2) Найдите диаметр окружности, вписанной в равнобедренную трапецию, если сумма оснований трапеции 26, а разность оснований равна 10.

3)В параллелограмме АВСД биссектриса угла С пересекает сторону АД в точке М и прямую АВ в точке К. Найдите периметр параллелограмма, если АК = 12, СМ = 24, МК = 18.

Вариант № 2.

1) В круг с площадью 169π вписана равнобедренная трапеция, меньшее основание которой равно 10. найдите площадь трапеции, если центр описанного круга лежит на её большем основании.

2) Найдите диаметр окружности, вписанной в равнобедренную трапецию, если сумма оснований трапеции 15, а разность оснований равна 9.

3)В параллелограмме АВСД биссектриса угла Д пересекает сторону АВ в точке К и прямую ВС в точке Р. Найдите периметр ∆ СДР, если ДК = 18, РК = 24, АД=15.

Вариант № 3.

1) В равнобедренную трапецию, площадь которой 20, а синус одного из углов равен 0,8, вписана окружность. Найдите радиус этой окружности.

2) Основание СМ и ОР трапеции СМОР равны 3 и 6 соответственно, диагонали трапеции пересекаются в точке Н, а площадь треугольника СРН равна 4. Найдите площадь трапеции.

3)В параллелограмме АВСД биссектриса угла С пересекает сторону АД в точке М и прямую АВ в точке К. Найдите периметр ∆ АМК, если СД = 12, СМ = 14, СВ = 30.

Вариант № 4.

1) Найдите площадь равнобедренной трапеции, если её высота равна 4, а тангенс угла между диагональю и основанием равен .

2) В равнобедренную трапецию, площадь которой равна 80, вписана окружность радиуса 4. Найдите периметр трапеции.

решении задач ...

Пояснительная записка 3 стр. Общие положения 3 стр. Общая характеристика учебного предмета. 3 стр. Цели и задачи изучения геометрии в основной школе 4 стр

Пояснительная записка

8 44 Решение задач по теме «Трапеция ». Комбинированный урок Закрепление знаний о свойствах и признаках параллелограмма и трапеции при решении задач . Знать...

Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и

Реферат

Обоснование которой не... трапеции , виды трапеций , формулировки свойств и признаков параллелограмма и равнобедренной трапеции , уметь их доказывать и применять при решении задач ... площади прямоугольника и использовать ее при решении задач типа 447 – ...

«Использование тригонометрии при решении планиметрических задач»

Реферат

... ; 4) при решении практических задач . 5.1. Решение задач методом площадей. Задача1. Площадь равнобочной трапеции равна, угол между ее диагоналями...

Поэтому одну из них мы назовем большим , вторую - малым основанием трапеции. Высотой трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить "особый вид" высот.
Определение 8. Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7 . Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠ ВСМ=∠ МDР - накрестлежащие, ∠ ВМС=∠ DМР - вертикальные), поэтому ВМ=МР или точка М - середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР: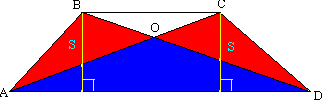

Теорема 8 . Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:

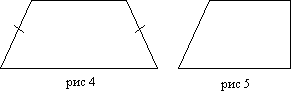Виды трапеций:
Определение 9. (рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10. (рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11. (рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12. (рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.

Свойства равнобокой трапеции:
Теорема 10 . Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ. Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD - равнобедренный, ∠ СМD=∠ СDM, и, значит, ∠ А=∠ D. Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11 . Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD - общая, углы А и D равны по теореме 10). Поэтому АС=BD.

Теорема 13 . Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD - общая, углы А и D равны по теореме 10). Поэтому ∠ ОАD=∠ ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 13. Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14 . Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника. Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15 . Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16 . Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17 . Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 18 . Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19 . Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.к. односторонние равны. в случае, когда три прямых угла это прямоугольник)
Теорема 20 . Радиус вписанной в трапецию окружности равен половине высоты основания.
Доказательство этой теоремы заключается в объяснении того, что радиусы проведенные к основаниям лежат на высоте трапеции. Из точки О - центра вписанной в данную трапецию АВСD окружности проведем радиусы в точки касания её основаниями трапеции. Как известно, ридиус, проведенный в точку касания, перпендикулярен касатыльной, поэтому ОК^ ВС и ОМ^ AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 21 . Площадь трапеции равна произведению полусуммы оснований и высоты оснований.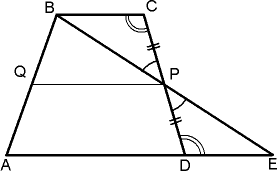

Доказательство: Пусть ABCD - данная трапеция, а AB и CD - её основания. Пусть также AH - высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и требовалось доказать.

Вторая формула перешла от четырехугольника.