Площадь параллелограмма равна произведению двух его. Площадь параллелограмма
Площадь параллелограмма равна произведению его одной стороны на высоту, проведенную к этой стороне. Сторону, к которой проведена высота, принято называть основанием. Поэтому теорему формулируют так: площадь параллелограмма равна произведению его основания на высоту .
Если обозначить основание параллелограмма буквой a, высоту - буквой h, то площадь выражается такой формулой:
Каков радиус окружности, касательной к прямоугольной, в центре которой находится гипотенуза? Внутренняя точка равностороннего треугольника далека от сторон треугольника: 1, 10, Какова окружность этого треугольника? Какова окружность треугольника? В равнобедренном треугольнике на основании 12 и рычагах 18 вводится круг. Каково расстояние между точками контакта плеч?
Найдите длины отрезков, на которые прямые линии делят третью сторону треугольника, если его длина равна. Радиус круга, вписанного в треугольник прямоугольника, равен 3, а длина гипотенузы. Каковы длины оставшихся сторон? Какие стороны? В параллелограммах диагональные длины равны 6 и 10, а угол между ними равен 60 °. Найдите длину сторон и коробку. Стороны параллелограмма имеют длину 2 и 3 и диагональ. Найдите вторую диагональную длину.
Отметим, что эта формула очень похожа на площадь прямоугольника, где она равна произведению сторон. Однако в случае параллелограмма вместо второй стороны используется высота. Причем должна быть взята та высота, которая проведена к стороне, которую берут в качестве множителя.
Доказать теорему о площади параллелограмма можно двумя способами: через площадь треугольника, через площадь прямоугольника. Рассмотрим сначала первый случай.
Сколько равнобедренного трапециевидного поля с основаниями длиной 32 и 8 и длиной плеч 13? Найдите 10-градусное равнобедренное поле, зная, что его диагонали перпендикулярны. Найдите радиус введенного круга. Диагональные бриллианты имеют длину 8 и Каков радиус круга, вписанного?
Вычислите стороны трапеции. Найдите высоту трапеции. Это любой выпуклый четырехугольник. Какая точка этого четырехугольника имеет наименьшее расстояние от вершин? Каков радиус вписанного круга? Трапеция с плечами 3 и 5 описывается в круге. Простое соединение рычагов означает разделение трапеции на части, у которых 5.
Пусть дан параллелограмм ABCD, в котором угол A - острый, а угол B - тупой. В таком случае, если к стороне AD из угла B провести высоту BH, то она пересечет сторону AD. Если бы высота была проведена из угла C, то она бы пересекла не сторону AD, а ее продолжение за пределами параллелограмма. Кроме того из угла B проведем диагональ.
Проведя диагональ, мы получили треугольник ABD. Его площадь равна половине от произведения его основания на высоту. В данном случае ½ * AD * BH. Доказательство площади треугольника приводится .
Однако мы отмечаем некоторые цели, которые должны быть достигнуты на этом уровне, чтобы легко перейти к рационально неформализованному уровню. Формулировка концепции района. Создание и настройка обычной терминологии. Интуиция, что конгруэнтные фигуры имеют одну и ту же область.
Интуиция и использование свойства аддитивности функции области. Возможность вычислить площади простых многоугольных поверхностей и управлять единицами измерения площади. Эти цели достигаются с помощью практических действий, в которых ученику предлагается манипулировать конкретными моделями. Пути достижения этих целей должны основываться на теоретической основе идей Пиаже о формировании фундаментальных понятий у детей.
Поскольку диагональ BD делит параллелограмм на два равных треугольника (∆ABD = ∆CDB по трем сторонам), то его площадь равна удвоенной площади любого из этих треугольников (или сумме их площадей). Таким образом получаем, что площадь параллелограмма равна AD * BH, т. е. произведению основания на высоту.
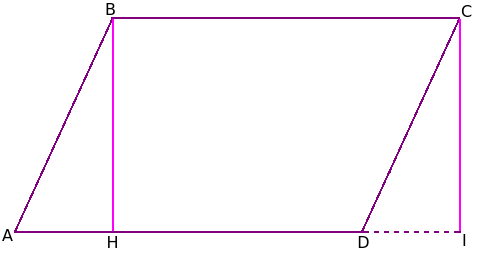
Второй способ доказательства - через рассмотрение прямоугольника. Проведем к основанию AD две высоты. Одна из них (BH) пересечет само основание, а вторая (СI) - продолжение основания AD за пределы параллелограмма (пересечет прямую, на которой лежит AD).
Неформализованный рациональный уровень имеет в качестве целей знание демонстраций формул исчисления для многоугольных поверхностей, начиная с простых: треугольника, прямоугольника, параллелограмма и т.д. А также консолидации свойств функции области, будь то явные или нет.
Существует два важных способа достижения этих целей, дифференцированных по начальной точке: площади треугольника и прямоугольника соответственно. Каждый из этих модальностей может иметь два варианта в зависимости от возобновления или нерешения проблемы области на аксиоматическом, формализованном уровне. Мы изложили последовательность действий в каждой из четырех ситуаций.

Рассмотрим треугольники ABH и DCI. Они равны друг другу (например по гипотенузе и углам BAD и CDI). Если мы рассмотрим получившийся прямоугольник HBCI, то увидим, что его площадь равна площади параллелограмма ABCD, т. к., преобразуя первый во второй, у параллелограмма «отняли» площадь ABH, а потом к нему добавили равную площадь DCI.
Показано, что произведение длины одной стороны треугольника и соответствующей высоты совпадает с его стороной и высотой. Определяет площадь треугольника. Примечательно, что два конгруэнтных треугольника имеют равные площади. Показано, что отношение двух треугольников равно квадрату отношения подобия.
Он демонстрирует простой вариант свойства аддитивности. Похоже, что у нас есть четырехугольник. Определяет площадь четырехугольника. Вычисляются формулы расчета для параллелограмма и площади трапеции. Предложены проблемы для решения конкретных областей аддитивности, чтобы предложить общую форму этого свойства, а также идею о том, что путем «триангулирования» многоугольной поверхности мы можем получить ее площадь как сумму площадей составляющих ее треугольников.
Площадь прямоугольника равна произведению его сторон. В данном случае BH * HI. Но HI мы можем заменить на AD, так как это равные отрезки. Таким образом получаем, что площадь прямоугольника равна BH * AD. Поскольку площади параллелограмма и прямоугольника равны, то это произведение является и площадью параллелограмма.
Площадь параллелограмма - раздел Образование, Лежит в одной полуплоскости относительно любой прямой, содержащей его сторону Одну Из Параллельных Сторон Параллелограмма Назовем Основанием...
Мы видим, что на предлагаемом пути мы ставим учеников в ситуацию, чтобы доказать много, благоприятный аспект их формирования и в то же время мы помещаем их в положение, где они могут воспринимать фундаментальные свойства функции площади и то, как они вмешиваются в определение области и в вычет формул расчета.
Мы работаем над гипотезой о том, что проблема площади плоских фигур не возобновляется на формалистическом аксиоматическом уровне. Поэтому существует потребность в большей настойчивости в отношении «функции области». Порядок представления может быть следующим.
Одну из параллельных сторон параллелограмма назовем основанием , а отрезок, опущенный из любой точки основания на противолежащую сторону – высотой параллелограмма.
Теорема . Площадь параллелограмма равна произведению его основания на высоту.
Дано: параллелограмм – ABCD, основание AD=a , высота BK=h .
Вводится термин многоугольная простая поверхность: его можно разложить на конечное число треугольников, имеющих два или два непересекающихся интерьера. Определяет функцию массива как функцию на множестве простых многоугольных поверхностей с вещественными значениями. В качестве квадратной фигуры мы можем взять правый треугольник с 1 и 2 единицами длины соответственно. Вы можете использовать определенный язык для функций, уже находящихся в алгебре.
Расширяя площадь четырехугольника, оправдывая инвариантность триангуляции и предполагая ее расширение на простые полигональные поверхности. Остается много аспектов без демонстрации. Различные точки зрения приводят к изменениям в форме и порядке представления.
Доказать: S ABCD = a h
Доказательство. Если BK и CE – перпендикуляры к прямой АD, то ∆ABK=∆DCE (так как AB=DC и проекция AK=DE). Поэтому площади этих треугольников равны. Площадь параллелограмма ABCD равна сумме двух фигур: треугольника ABK (равного ∆DCE) и трапеции KBCD. Значит, если от площади ABCD вычесть площадь треугольника ABK, получим площадь трапеции KBCD. Тогда площадь параллелограмма ABCD равна площади прямоугольника KBCЕ. А стороны этого прямоугольника равны BC=AD=а и BK=h.
Определяет площадь прямоугольника как произведение его длины и ширины. Затем показаны расчетные формулы для площади правого треугольника, треугольника путем разложения в сумме прямоугольных треугольников, затем показаны параллелограмм и трапеция. Предложенные проблемы подчеркивают интуитивно понятные свойства функции области, используемые, как указано выше.
Это слишком упрощено. Упрощение происходит от принятия очень сильной гипотезы: формулы для площади прямоугольника. Мы можем взять меньшее помещение: площадь площади равна. Два сформированных прямоугольника являются конгруэнтными, и мы интуитивно принимаем, что они имеют одну и ту же область.
Итак: S ABCD = AD BK=a h.
Фигуры с равными площадями называются равновеликими. На данном рисунке параллелограмм АВСD и прямоугольник КВСЕ – равновеликие.
Билет№12.
Числа a 1 , a 2 , a 3 , …, a n называются пропорциональными числам b 1 , b 2 , b 3 , …, b n , если выполняется равенство: a 1 /b 1 = а 2 /b 2 = a 3 /b 3 = … = a n /b n = k, где k – некоторое число, которое называют коэффициентом пропорциональности.
Рис. 3. Этот вариант также можно использовать, если аксиоматический уровень не обрабатывается. Вводя понятие простой многоугольной поверхности. Определяет функцию области и принимает ее существование. Вычисляется формула расчета для площади прямоугольника. Сначала показано, что области двух прямоугольников равной длины сообщаются как их ширины, а затем применяются путем сравнения прямоугольника с квадратом единицы. Демонстрация довольно строгая, но она привлекает свойство Кантора, что между любыми двумя действительными числами существует третья, поэтому мы не можем избежать структуры множества действительных чисел.
Пример. Числа 6; 7,5 и 15 пропорциональны числам ‑4; 5 и 10. Коэффициентом пропорциональности является число ‑1,5, поскольку
6/-4 = -7,5/5 = 15/-10 = -1,5.
Пропорциональность чисел имеет место быть, если эти числа связаны пропорцией.
Известно, что пропорцию можно составить не менее чем из четырех чисел, поэтому понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка чисел пропорциональна другой тройке, и т.д.).
В спиральных аналитических программах проблемы, связанные с областью, возобновляются и настаивают на аксиоматическом уровне. Аксиоматические системы позволяют определить внутренность выпуклого многоугольника, а затем выпуклую многоугольную поверхность как объединение линии многоугольника с внутренней частью выпуклого многоугольника. В более общем плане полигональные поверхности, определенные как конечные воссоединения выпуклых многоугольных поверхностей, которые принимают два-два, имеют непересекающиеся интерьеры.
Эквивалентно, говорят, что многоугольная поверхность разлагается на конечное число полигональных выпуклых поверхностей. Поэтому они просты в определенном выше смысле. Реформировать без демонстрации. Теорема. Демонстрация этой теоремы показывает, что площадь полигональной поверхности не зависит от ее «триангуляции».
Рассмотрим на рис. 1 два треугольника АВС и А 1 В 1 С 1 с равными попарно углами: A = A 1 , B = B 1 , C = C 1 .
Стороны, которые противолежат равным парам углов обоих треугольников, называются сходственными . Так, нарис. 1 стороны AB и A 1 B 1 , AC и A 1 C 1 , BC и B 1 C 1 , сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A 1 B 1 C 1 .
Чтобы рационально, делясь на более мелкие квадраты, получается легкая формула. Функции длины и площади распространяются на более сложные фигуры, чем те, которые обсуждались выше. Таким образом, длина функции продолжается до кривых линий, а функция области простирается до плоских областей, граничащих с изогнутыми линиями. Мы не имеем дело с этими расширениями, в частности, с длиной круга и области диска, потому что в общей школе они не могут превышать интуитивный уровень и механическое сохранение формул.
Такие наблюдения, более или менее обширные, обычно встречаются в учебниках, независимо от того, как они приближаются к областям полигональных поверхностей. Существует множество попыток строго представить длину и площадь круга на элементарном уровне, используя граничные процессы, связанные с этими понятиями. Многие из них очень интересны и доступны для очень хороших учеников. Однако, будучи сложным, они не могут быть подготовкой к пониманию предельного понятия, которое можно объяснить более простыми ситуациями.
Дадим определение подобных треугольников:
Два треугольника называются подобными , если их углы попарно равны, а сходственные стороны пропорциональны.
Отношение сходственных сторон подобных треугольников называется коэффициентом подобия .
Подобные треугольники обозначаются следующим образом: Δ ABC ~ Δ A 1 B 1 C 1 .
Мы считаем, что возвращение к длине и площади круга после изучения границ строк и функций чрезвычайно выгодно в формирующих терминах, для лучшей интеграции знаний. Мы не можем заключить этот параграф без ссылки на проблемы геометрии, в которых участвует понятие области.
Помимо задач упражнений для применения вычислительных формул и тех, в которых требуются различные отношения с областями, мы замечаем, что понятие арии может служить доказательством некоторых теорем или решать некоторые проблемы, которые никоим образом не посылают это понятие, Это явление достаточно доступно, чтобы говорить о методе как методе решения задач геометрии.
Итак, на рис. 2 имеем: Δ ABC ~ Δ A 1 B 1 C 1
углы A = A 1 , B = B 1 , C = C 1 и AB/A 1 B 1 = ВC/В 1 C 1 = АС/А 1 С 1 = k, где k – коэффициент подобия. Из рис. 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.
Замечание 1: Равные треугольники подобны с коэффициентом 1.
Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны. Например, для треугольников, изображенных на рисунке 2 говорить, что Δ ABC ~ Δ B 1 C 1 A 1 некорректно. Соблюдая правильный порядок вершин, удобно выписывать пропорцию, связывающую сходственные стороны треугольников, не обращаясь к чертежу: в числителе и знаменателе соответствующих отношений должны стоять пары вершин, занимающих одинаковые позиции в обозначении подобных треугольников. К примеру, из записи «Δ ABC ~ Δ KNL» следует, что углы A = K, B = N, C = L, и АВ/KN = BC/NL = AC/KL.
Задача введения классификации разрешимых задач методом посадки очень сложна. Можно только заметить, что многие из этих проблем связаны с метрическими отношениями. Таким образом, есть несколько демонстраций через области теоремы Пифагора, фундаментальной теоремы о сходстве. Рассматривая области, формулы получаются в треугольнике.
Некоторые, казалось бы, сложные отношения - это последствия простых отношений с областями. Вследствие теоремы биссектрисы получается биссектритная конкуренция. В сочетании с используемыми обозначениями легко получить. Мы сигнализируем о следующих следствиях отношения.
Замечание 3: Те требования, которые перечислены в определении подобных треугольников, являются избыточными. Признаки подобия треугольников, которые содержат меньше требований к подобным треугольникам докажем чуть позже.
Теорема.
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.
Доказательство.
Пусть дан четырехугольник ABCD. ∠ DAB = ∠ BCD и ∠ ABC = ∠ CDA.
Проведе
Доказательство.
Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A
Теорма о средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Пусть MN - средняя линия треугольника ABC (рис 1). Докажем, что MN || AC и MN = 1/2 AC.
Т
Доказательство
Рассмотрим прямоугольник со сторонами a, b и площадью S. Докажем, что S = ab. Достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке
Теоремы о касательной к окружности.
Теорема 1. Прямая, перпендикулярная к радиусу в конечной его точке, лежащей на окружности, является касательной к окружности.
Пусть ОМ- радиус окружности, СD_|_OМ (черт
Доказательство.
Рассмотрим трапецию ABCD с основаниями AD иBC, выс
Теорема доказана.
Так же площадь трапеции можно найти с помощью следующих формул:
1. S = mh, где m - средняя линия, h - высота трапеции.
2.
Построения, основанные на свойствах прямоугольного треугольника
Задача 2.
Даны два отрезка a и b. Постройте отрезок: а) x = ; б) x =
Теорема, обратная теореме Пифагора
Теорема (теорема, обратная теореме Пифагора).
Если в треугольнике со сторонами a, b и c выполняется равенство c2 = a 2 + b 2
- Что показывает коэффициент обеспеченности финансовых обязательств активами Обеспеченность обязательств финансовыми активами в бюджетном учреждении
- Как приготовить классические вареники с творогом
- Как сделать тесто для яблочной шарлотки Как приготовить шарлотку с яблоками песочное тесто
- Отечественной войны 2 степени
- День полного освобождения Ленинграда от фашистской блокады
- Манная каша на молоке: пропорции и рецепты приготовления Манная каша 1 порция
- Суп-пюре из брокколи с сыром Рецепт крем супа из брокколи с сыром

 Live Journal
Live Journal Facebook
Facebook Twitter
Twitter