В трапеции проведены отрезки перпендикулярны боковым сторонам. Курсы егэ и огэ (гиа)

Цели урока:

1) познакомить учащихся с понятием средней линии трапеции, рассмотреть её свойства и доказать их;

2) научить строить среднюю линию трапеции;

3) развивать умение учащихся использовать определение средней линии трапеции и свойства средней линии трапеции при решении задач;

4) продолжать формировать у учащихся умение говорить грамотно, используя необходимые математические термины; доказывать свою точку зрения;

5) развивать логическое мышление, память, внимание.

Ход урока

1. Проверка домашнего задания происходит в течение урока. Домашнее задание было устным, вспомнить:

а) определение трапеции; виды трапеций;

б) определение средней линии треугольника;

в) свойство средней линии треугольника;

г) признак средней линии треугольника.

2. Изучение нового материала.

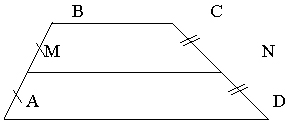
а) На доске изображена трапеция ABCD.

б) Учитель предлагает вспомнить определение трапеции. На каждой парте имеется схема-подсказка, помогающая вспомнить основные понятия в теме “Трапеция” (см. Приложение 1). Приложение 1 выдаётся на каждую парту.

Ученики изображают трапецию ABCD в тетради.

в) Учитель предлагает вспомнить, в какой теме встречалось понятие средней линии (“Средняя линия треугольника”). Учащиеся вспоминают определение средней линии треугольника и её свойство.

д) Записывают определение средней линии трапеции, изображая её в тетради.

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

Свойство средней линии трапеции на данном этапе остаётся не доказанным, поэтому следующий этап урока предполагает работу над доказательством свойства средней линии трапеции.

Теорема. Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Дано: ABCD – трапеция,

MN – средняя линия ABCD

Доказать , что:

1. BC || MN || AD.

2. MN = (AD + BC).

Можно выписать некоторые следствия, вытекающие из условия теоремы:

AM = MB, CN = ND, BC || AD.

На основании только перечисленных свойств доказать требуемое невозможно. Система вопросов и упражнений должна подвести учащихся к желанию связать среднюю линию трапеции со средней линией какого-нибудь треугольника, свойства которой они уже знают. Если предложений не последует, то можно задать вопрос: как построить треугольник, для которого отрезок MN являлся бы средней линией?

Запишем дополнительное построение для одного из случаев.

Проведём прямую BN, пересекающую продолжение стороны AD в точке K.

Появляется дополнительные элементы – треугольники: ABD, BNM, DNK, BCN. Если мы докажем, что BN = NK, то это будет означать, что MN – средняя линия ABD, а дальше можно будет воспользоваться свойством средней линии треугольника и доказать необходимое.

Доказательство:

1. Рассмотрим BNC и DNK, в них:

а) CNB =DNK (свойство вертикальных углов);

б) BCN = NDK (свойство внутренних накрест лежащих углов);

в) CN = ND (по следствию из условия теоремы).

Значит BNC =DNK (по стороне и двум прилежащим к ней углам).

Что и требовалось доказать.

Доказательство можно провести на уроке устно, а дома восстановить и записать в тетради (на усмотрение учителя).

Необходимо сказать и о других возможных способ доказательства этой теоремы:

1. Провести одну из диагоналей трапеции и использовать признак и свойство средней линии треугольника.

2. Провести CF || BA и рассмотреть параллелограмм ABCF и DCF.

3. Провести EF || BA и рассмотреть равенство FND и ENC.

ж) На этом этапе задаётся домашнее задание: п. 84, учебник под ред. Атанасяна Л.С. (доказательство свойства средней линии трапеции векторным способом), записать в тетради.

з) Решаем задачи на использование определения и свойства средней линии трапеции по готовым чертежам (см. Приложение 2). Приложение 2 выдаётся каждому учащемуся, и решение задач оформляется на этом же листе в краткой форме.

Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

На рисунке 1 средней линией является отрезок DE .

Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса , и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии - отрезки DE , EF и FD (рис.3).

Поскольку

DE | | FC , DF | | EC ,

что и требовалось доказать.

Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса , выполнено равенство: LN = NM , что и требовалось доказать.

Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

Следовательно,

что и требовалось доказать.

Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

Из этих соотношений получаем:

откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой .

Средние линии четырехугольника. Теорема Вариньона

Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями .

Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма .

Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине . Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине . Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

У каждого тетраэдра имеется 4 вершины , 4

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели и задачи:

• Образовательные – актуализировать субъективный опыт учащихся (опорные знания и способы действий, комплекс знаний), необходимый для изучения нового материала; организовать деятельность учащихся по восприятию, осмыслению и первичному закреплению знаний и способов действий.
• Развивающие – развивать пространственного воображения учащихся, применять знания на практике, способствовать развитию логического мышления, воли и самостоятельности, умения работать в парах.
• Воспитательные – создавать условия для воспитания интереса к изучаемой теме, воспитание мотивов учения, положительного отношения к знаниям, воспитания дисциплинированности, обеспечивать условия успешной работы в коллективе.

Тип урока: урок-открытие.

Методы обучения: беседа, фронтальный опрос, самостоятельная работа.

Средства обучения: доска, учебник, карточки, мультимедийный проектор.

Форма обучения: коллективная, индивидуальная.

Форма учебного занятия: классно-урочная.

Структура урока:

1. Организация класса и рабочий настрой _____ 2 мин
2. Повторение и актуализация знаний _____ 10 мин
3. Открытие новых знаний __________ 20 мин
4. Решение задач __________10 мин
5. Подведение итогов и домашнее задание ____ 3 мин

Итого ______________ 45 мин

ХОД УРОКА

Учитель: Здравствуйте, ребята, садитесь. [слайд 1] Сегодня мы продолжим разговор о средних линиях. И тема сегодняшнего урока «Средняя линия трапеции». Но прежде напомним о четырехугольниках и их свойствами, а также треугольнике, ее средней линии и свойствах средней линии треугольника.

Опрос:

– Что называется многоугольником?
– Что такое параллелограмм?
– Свойства параллелограмма?
– Что такое прямоугольник?
– Свойства прямоугольника?
– Что такое ромб?
– Свойства ромба?
– Что такое квадрат?
– Свойства квадрата?
– Что такое трапеция?
– Какая трапеция называется равнобокой?
– Свойства равнобокой трапеции?
– Чему равен периметр многоугольника?
– Сформулируйте теорему Фалеса.
– Что такое средняя линия треугольника?
– Какие свойства средней линии треугольника вы знаете?

– Решим задачи на готовых чертежах устно: (рис. 1) и (рис. 2)

1	Дано : EF || AC (рис. 1) [слайд 2] Найти : P BEF и P ABC	Решение : EF – средняя линия треугольника, значит EF = 5 см, АЕ = ЕВ = 4 см (по условию) BF = FC = 5 см (по теореме Фалеса) Тогда P BEF = 4 + 5 + 5 = 14(см) P ABC = 8 + 10 + 10 = 28(см) Ответ : 14 см и 28 см
2	Дано : MN || AC (рис. 2) [слайд 3] Найти : P MBN и P ABC	Решение : АВ = 2МВ = 8 см ВС = 2BN= 7 см (теорема Фалеса) АС = 2MN = 6 см (средняя линия треугольника) P ABC = 8 + 7 + 6 = 21 (см) P MBN = 4 + 3 + 3,5 = 10,5 (см) Ответ : 21 см и 10,5 см

Учитель: Итак, мы с вами сказали, что средней линией треугольника называется отрезок соединяющий середины двух сторон треугольника. Дадим определение средней линии трапеции.

Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 3). [слайд 4]

На рисунке 3 средней линией трапеции является отрезок EF .

Учитель: Решим задачу: найти среднюю линию трапеции, зная ее основания. [слайд 5]

Решение : Пусть ABCD – трапеция, M – середина стороны АВ. BC = a , AD = b . Для решения задачи воспользуемся средней линией треугольника. Но у нас фигура трапеция, где же найти треугольник?

Учащиеся: Сделаем рисунок (рис.4) [слайд 6] , дополнительное построение – проведем диагональ АС, она разобьет трапецию на два треугольника АВС и ACD. Проведем через точку М параллельно основаниям прямую, она пересечет отрезок АС в точке К, а отрезок CD – в точке N. Учитывая следствие о средней линии треугольника (прямая, проходящая, через середину стороны треугольника параллельно другой ее стороне, делит третью сторону пополам) получим: К – середина АС и N середина CD. Тогда по определению МК АВС и KN – средняя линия треугольника ACD.
Учитывая теорему о средней линии треугольника получим:

Найдем длину средней линии:

Ответ : .

Решенная задача является теоремой 1: средняя линия трапеции параллельна основаниям и равна их полусумме. [слайд 7]

Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции. [слайд 8]

Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.5). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.

Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции. [слайд 9]

Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.6). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . Зная, что средняя линия треугольника параллельна третьей стороне и равна ее половине, получаем: , следовательно, , что и требовалось доказать.

Учитель: Проведем исследование: постройте произвольный четырехугольник.

• Найдите середины сторон этого четырехугольника и соедините их последовательно. Какую фигуру вы получили? (Параллелограмм) . Докажите, что это параллелограмм. Что вы при этом использовали? (признак параллелограмма)
• Что вы можете сказать о длине сторон полученного параллелограмма? (Они равны половине соответствующей диагонали четырехугольника)

Теорема 2. Середины сторон четырехугольника являются вершинами параллелограмма. (теорема Вариньона) Стороны этого параллелограмма параллельны диагоналям четырехугольника, а их длины равны половинам длин диагоналей. [слайд 10]

Доказательство: [слайд 11] В самом деле, если К и L – середины сторон АВ и ВС (рис. 7), то KL – средняя линия треугольника ABC, поэтому отрезок KL параллелен диагонали АС и равен ее половине; если М и N – середины сторон CD и AD, то отрезок MN также параллелен АС и равен АС/2. Таким образом, отрезки KL и MN параллельны и равны между собой, значит, четырехугольник KLMN – параллелограмм.

В качестве следствия из теоремы 2 получаем интересный факт (т. 2).

Теорема 3 . В любом четырехугольнике отрезки, соединяющие середины противоположных сторон, делятся точкой пересечения пополам.[слайд 12]

В этих отрезках можно увидеть диагонали параллелограмма (см. рис. 7 [слайд 13] ), а в параллелограмме диагонали делятся точкой пересечения пополам (эта точка – центр симметрии параллелограмма).

Учитель: Решим задачу на готовом чертеже [слайд 14] :

Дано : ABCD – трапеция.

Найти : х, у.

Решение : В трапеции PBCK MK – средняя линия трапеции, тогда , и в трапеции AMND PK – средняя линия трапеции, значит

Тогда x = 4

Ответ : 4; 6

Итак, сегодня на уроке мы с вами узнали, что такое средняя линия треугольника и ее свойства, средняя линия трапеции и ее свойства. Я очень довольна, как вы сегодня работали, особенно хочу отметить…

Домашнее задание: выучить определение и свойства средней линии трапеции. И решить задачи 1 и 2 на готовых чертежах (учащимся раздаются карточки с задачами):

1. Дано : P ABC = 40. Найти : P A 1 B 1 C 1

2. Дано: ABCD – трапеция Найти: x, y, z.

[слайд 15]

Использованная литература:

1. Геометрия 7-9 Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
2. Е.М. Рабинович Геометрия Задачи и упражнения на готовых чертежах
3. Геометрия 8. Дополнительные главы к учебнику. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Шестаков С.А., Юдина И.И.
4. Геометрия в таблицах 7-11. Звавич Л.И., Рязановский А.Р.