Формула когда дискриминант равен нулю. Решение квадратных уравнений с отрицательными дискриминантами. Варианты расчётов для закрепления материала

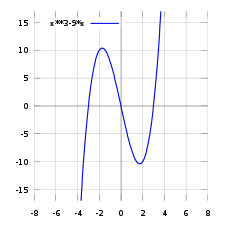
Важно! В корнях четной кратности функция знак не меняет.

Обратите внимание! Любое нелинейное неравенство школьного курса алгебры нужно решать с помощью метода интервалов.

Предлагаю вам подробный алгоритм решения неравенств методом интервалов , следуя которому вы сможете избежать ошибок прирешении нелинейных неравенств .

Решение квадратных уравнений с отрицательными дискриминантами

Как мы знаем,

i 2 = - 1.

Вместе с тем

(- i ) 2 = (- 1 i ) 2 = (- 1) 2 i 2 = -1.

Таким образом, существуют по крайней мере два значения корня квадратного из - 1, а именно i и - i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны - 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен - 1. Тогда

(а + bi ) 2 = - 1,

а 2 + 2аbi - b 2 = - 1

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

{	а 2 - b 2 = - 1 ab = 0 (1)

Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а 2 = - 1. Число а действительное, и поэтому а 2 > 0. Неотрицательное число а 2 не может равняться отрицательному числу - 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем: -b 2 = - 1, b = ± 1.

Следовательно, комплексными числами, квадраты которых равны -1, являются только числа i и -i , Условно это записывается в виде:

√-1 = ± i .

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу -а . Такими числами являются √ai и -√ai . Условно это записывается так:

√- а = ± √ai .

Под √a здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2, √9 =.3; поэтому

√-4 = + 2i , √-9= ± 3i

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x 2 + 2х + 5 = 0; тогда

х 1,2 = - 1 ± √1 -5 = - 1 ± √-4 = - 1 ± 2i .

Итак, данное уравнение имеет два корня: х 1 = - 1 +2i , х 2 = - 1 - 2i . Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна - 2, а произведение 5, так что выполняется теорема Виета.

Понятие комплексного числа

Комплексным числом называется выражение вида a + ib , где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1. Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
   a = b и c = d .
2. Суммой двух комплексных чисел a + ib и c + id называется комплексное число
   a + c + i (b + d).
3. Произведением двух комплексных чисел a + ib и c + id называется комплексное число
   ac – bd + i (ad + bc).

Комплексные числа часто обозначают одной буквой, например, z = a + ib . Действительное число a называется действительной частью комплексного числа z , действительная часть обозначается a = Re z . Действительное число b называется мнимой частью комплексного числа z , мнимая часть обозначается b = Im z . Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.

Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,

Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что , а именно

В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi , например, 0 + i 3 = 3 i . Чисто мнимое число i1 = 1 i = i обладает удивительным свойством:
Таким образом,

№ 4 .1. В математике числовая функция - это функция, области определения и значений которой являются подмножествами числовых множеств - как правило, множествавещественных чисел или множества комплексных чисел .

График функции

Фрагмент графика функции

Способы задания функции

[править]Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.

[править]Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:

[править]Графический способ

Осциллограмма задаёт значение некоторой функции графически.

Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.

[править]Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

• факториал;
• числа Фибоначчи;
• функция Аккермана.

[править]Словесный способ

Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.

• функция, возвращающая цифру в записи числа пи по её номеру;
• функция, возвращающая число атомов во вселенной в определённый момент времени;
• функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождени

Дискриминант – многозначный термин. В данной статье речь пойдёт о дискриминанте многочлена, который позволяет определить, есть ли у данного многочлена действительные решения. Формула для квадратного многочлена встречается в школьном курсе алгебры и анализа. Как найти дискриминант? Что нужно для решения уравнения?

Квадратным многочленом или уравнением второй степени называется i * w ^ 2 + j * w + k равный 0, где “i” и “j” – первый и второй коэффициент соответственно, “k” – константа, которую иногда именуют “свободным членом”, а “w” – переменная. Его корнями окажутся все значения переменной, при которых оно превращается в тождество. Такое равенство допустимо переписать, как произведение i, (w – w1) и (w – w2) равное 0. В этом случае очевидно, что если коэффициент “i” не обращается в ноль, то функция в левой части станет нулевой только в случае, если x принимает значение w1 или w2. Эти значения являются результатом приравнивания многочлена к нулю.

Для нахождения значения переменной, при котором квадратный многочлен обращается в ноль, используется вспомогательная конструкция, построенная на его коэффициентах и названная дискриминантом. Эта конструкция рассчитывается согласно формуле D равняется j * j – 4 * i * k. Зачем она используется?

1. Она говорит, имеются ли действительные результаты.
2. Она помогает их высчитать.

Как это значение показывает наличие вещественных корней:

• Если оно положительное, то можно найти два корня в области действительных чисел.
• Если дискриминант равен нулю, то оба решения совпадают. Можно сказать, что есть всего одно решение, и оно из области вещественных чисел.
• Если дискриминант меньше нуля, то у многочлена отсутствуют вещественные корни.

Варианты расчётов для закрепления материала

Для суммы {7 * w ^ 2; 3 * w; 1} равной 0 рассчитываем D по формуле 3 * 3 – 4 * 7 * 1 = 9 – 28 получаем -19. Значение дискриминанта ниже нуля говорит об отсутствии результатов на действительной прямой.

Если рассмотреть 2 * w ^ 2 – 3 * w + 1 эквивалентный 0 , то D рассчитывается как (-3) в квадрате за вычетом произведения чисел {4; 2; 1} и равняется 9 – 8, то есть 1. Положительное значение говорит о двух результатах на вещественной прямой.

Если взять сумму {w ^ 2; 2 * w; 1} и прировнять к 0 , D рассчитается, как два в квадрате минус произведение чисел {4; 1; 1}. Это выражение упростится до 4 – 4 и обратится в ноль. Выходит, что результаты совпадают. Если внимательно вглядеться в данную формулу, то станет понятно, что это “полный квадрат”. Значит, равенство можно переписать в форме (w + 1) ^ 2 = 0. Стало очевидно, что результат в этой задаче “-1”. В ситуации если D равен 0, левую часть равенства всегда получится свернуть по формуле “квадрат суммы”.

Использование дискриминанта в вычислении корней

Эта вспомогательная конструкция не только показывает количество вещественных решений, но и помогает их находить. Общая формула расчёта для уравнения второй степени такова:

w = (-j +/- d) / (2 * i), где d – дискриминант в степени 1/2.

Допустим, дискриминант ниже нулевой отметки, тогда d – мнимо и результаты мнимые.

D нулевой, тогда d, равный D в степени 1/2, тоже нулевой. Решение: -j / (2 * i). Снова рассматриваем 1 * w ^ 2 + 2 * w + 1 = 0, находим результаты эквивалентные -2 / (2 * 1) = -1.

Предположим, D > 0, значит, d – вещественное число, и ответ здесь распадается на две части: w1 = (-j + d) / (2 * i) и w2 = (-j – d) / (2 * i). Оба результата окажутся действительные. Взглянем на 2 * w ^ 2 – 3 * w + 1 = 0. Здесь дискриминант и d – единицы. Выходит, w1 равняется (3 + 1) делить (2 * 2) или 1, а w2 равен (3 – 1) делить на 2 * 2 или 1/2.

Результат приравнивания квадратного выражения к нулю вычисляется согласно алгоритму:

1. Определение количества действительных решений.
2. Вычисление d = D ^ (1/2).
3. Нахождение результата в соответствии с формулой (-j +/- d) / (2 * i).
4. Подстановка полученного результата в исходное равенство для проверки.

Некоторые частные случаи

В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство. Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:

1. многочлен раскладывается в разность квадратов при отрицательном свободном члене;
2. при положительной константе действительных решений найти нельзя.

Если свободный член нулевой, то корни будут {0; -j}

Но есть и другие частные случаи, упрощающие нахождение решения.

Приведенное уравнение второй степени

Приведенным именуют такой квадратный трёхчлен, где коэффициент перед старшим членом – единица. Для данной ситуации применима теорема Виета, гласящая, что сумма корней равняется коэффициенту при переменной в первой степени, помноженному на -1, а произведение соответствует константе “k”.

Следовательно, w1 + w2 равно -j и w1 * w2 равняется k, если первый коэффициент - единица. Чтобы убедиться в правильности такого представления, можно выразить из первой формулы w2 = -j – w1 и подставить его во второе равенство w1 * (-j – w1) = k. В итоге получается исходное равенство w1 ^ 2 + j * w1 + k = 0.

Важно отметить , что i * w ^ 2 + j * w + k = 0 удастся привести путём деления на “i”. Результат будет: w ^ 2 + j1 * w + k1 = 0, где j1 равно j / i и k1 равно k / i.

Взглянем на уже решенное 2 * w ^ 2 – 3 * w + 1 = 0 с результатами w1 = 1 и w2 = 1/2. Надо поделить его пополам, в итоге w ^ 2 – 3/2 * w + 1/2 = 0. Проверим, что для найденных результатов справедливы условия теоремы: 1 + 1/2 = 3/2 и 1*1/2 = 1/2.

Чётный второй множитель

Если множитель при переменной в первой степени (j) делится на 2 , то удастся упростить формулу и искать решение через четверть дискриминанта D/4 = (j / 2) ^ 2 – i * k. получается w = (-j +/- d/2) / i, где d/2 = D/4 в степени 1/2.

Если i = 1, а коэффициент j – чётный, то решением будет произведение -1 и половины коэффициента при переменной w, плюс/минус корень из квадрата этой половины за вычетом константы “k”. Формула: w = -j / 2 +/- (j ^ 2 / 4 – k) ^ 1/2.

Более высокий порядок дискриминанта

Рассмотренный выше дискриминант трёхчлена второй степени – это наиболее употребимый частный случай. В общем же случае дискриминант многочлена представляет собой перемноженные квадраты разностей корней этого многочлена . Следовательно, дискриминант равный нулю говорит о наличии как минимум двух кратных решений.

Рассмотрим i * w ^ 3 + j * w ^ 2 + k * w + m = 0.

D = j ^ 2 * k ^ 2 – 4 * i * k ^ 3 – 4 * i ^ 3 * k – 27 * i ^ 2 * m ^ 2 + 18 * i * j * k * m.

Допустим, дискриминант превосходит ноль . Это значит, что имеется три корня в области действительных чисел. При нулевом есть кратные решения. Если D < 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень – вещественный.

Видео

Наше видео подробно расскажет о вычислении дискриминанта.

Не получили ответ на свой вопрос? Предложите авторам тему.