Решение уравнений степени выше второй. Решение уравнений высших степеней различными методами
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Уравнения высших степеней (корни многочлена от одной переменной).
П лан лекции. № 1 . Уравнения высших степеней в школьном курсе математики. № 2 . Стандартный вид многочлена. № 3 .Целые корни многочлена. Схема Горнера. № 4. Дробные корни многочлена. № 5. Уравнения вида: (х + а)(х + в)(х + с) … = А № 6. Возвратные уравнения. № 7. Однородные уравнения. № 8. Метод неопределенных коэффициентов. № 9. Функционально – графический метод. № 10. Формулы Виета для уравнений высших степеней. № 11. Нестандартные методы решения уравнений высших степеней.
Мы используем функцию косинуса дуги! Чтобы использовать приведенный выше пример, мы имеем. В обоих случаях у нас есть определенный символ, который дает одно из решений и из этого решения, мы перестраиваем все остальные. Итак, вот два примера уравнений с косинусом.
Операция идентична для синуса. 
Итак, если мы имеем следующее уравнение. 
Вы заметили, что в отличие от косинуса и синуса тангенс проходит через все значения. Итак, вы решаете следующее уравнение. Как мы уже делали с элементарными операциями, речь шла о возвращении к неизвестному, следуя зеленому маршруту справа налево.
Уравнения высших степеней в школьном курсе математики. 7 класс. Стандартный вид многочлена. Действия с многочленами. Разложение многочлена на множители. В обычном классе 42 часа, в спец классе 56 часов. 8 спецкласс. Целые корни многочлена, деление многочленов, возвратные уравнения, разность и сумма п – ых степеней двучлена, метод неопределенных коэффициентов. Ю.Н. Макарычев « Дополнительные главы к школьному курсу алгебры 8 класса», М.Л.Галицкий Сборник задач по алгебре 8 – 9 класс». 9 спецкласс. Рациональные корни многочлена. Обобщенные возвратные уравнения. Формулы Виета для уравнений высших степеней. Н.Я. Виленкин « Алгебра 9 класс с углубленным изучением. 11 спецкласс. Тождественность многочленов. Многочлен от нескольких переменных. Функционально – графический метод решения уравнений высших степеней.
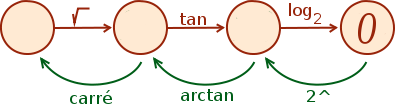
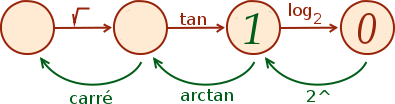
Чтобы подняться по касательной, мы используем касательную дугу. 
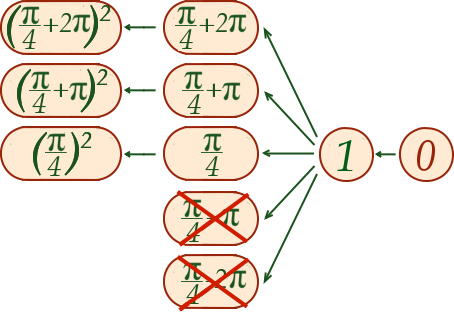
На диаграмме представлено только пять решений, но мы не должны забывать, что существует бесконечность. Все, что вам нужно сделать, это вернуться к корню, помните, что есть только решение, когда результат корня положителен, так что половина чисел, заданных нам касательной, не имеет выхода.
Мы только что решили наше уравнение благодаря нашим схемам, но, разумеется, те же рассуждения можно сделать только в алгебраическом письме. В школе для животных есть 3 котята, 4 утята, 1 собака и несколько ягнят. Что все его ученики имели в общей сложности 44 ноги.
Стандартный вид многочлена. Многочлен Р(х) = а ⁿ х ⁿ + а п-1 х п-1 + … + а₂х ² + а₁х + а₀. Называется многочленом стандартного вида. а п х ⁿ - старший член многочлена а п - коэффициент при старшем члене многочлена. При а п = 1 Р(х) называется приведенным многочленом. а ₀ - свободный член многочлена Р(х). п – степень многочлена.
Целые корни многочлена. Схема Горнера. Теорема № 1. Если целое число а является корнем многочлена Р(х), то а – делитель свободного члена Р(х). Пример № 1 . Решите уравнение. Х⁴ + 2х³ = 11х² – 4х – 4 Приведем уравнение к стандартному виду. Х⁴ + 2х³ - 11х² + 4х + 4 = 0. Имеем многочлен Р(х) = х ⁴ + 2х³ - 11х² + 4х + 4 Делители свободного члена: ± 1, ± 2, ±4. х = 1 корень уравнения т.к. Р(1) = 0, х = 2 корень уравнения т.к. Р(2) = 0 Теорема Безу. Остаток от деления многочлена Р(х) на двучлен (х – а) равен Р(а). Следствие. Если а – корень многочлена Р(х), то Р(х) делится на (х – а). В нашем уравнении Р(х) делится на (х – 1) и на (х – 2), а значит и на (х – 1) (х – 2). При делении Р(х) на (х ² - 3х + 2) в частном получается трехчлен х ² + 5х + 2 = 0, который имеет корни х =(-5 ± √17)/2
Животные с четырьмя ногами - 3 1 = 4, количество ног 4 = 16. Животные с двумя ногами - 4, количество ног 2 = 8. Поэтому ягнята 5, потому что 4 = 20. Лесоводство посеяло 87 фруктовых саженцев двумя способами. Первый путь посеяно 10 деревьев в ряд, а второй - 11 саженцев на линию. Сколько рядов выберет все саженцы саженцев.
Тогда 7 1 = 8 - общее количество строк в обоих направлениях. Котята пошли трое - один брат, две сестры. Они встретили две лопатки в десяти футах. Как только мыши останавливаются, котята обманчивы, а как «герои» они прячутся в тернии. Сколько ног вы ходите на тернии?
Дробные корни многочлена. Теорема №2. Если р / g корень многочлена Р(х), то р – делитель свободного члена, g – делитель коэффициента старшего члена Р(х). Пример № 2. Решите уравнение. 6х³ - 11х² - 2х + 8 = 0. Делители свободного члена: ±1, ±2, ±4, ±8. Ни одно из этих чисел не удовлетворяет уравнению. Целых корней нет. Натуральные делители коэффициента старшего члена Р(х): 1, 2, 3, 6. Возможные дробные корни уравнения: ±2/3, ±4/3, ±8/3. Проверкой убеждаемся, что Р(4/3) = 0. Х = 4/3 корень уравнения. По схеме Горнера разделим Р(х) на (х – 4/3).
Задача В кондитерской «Рождественская звезда» все столы имеют 4 ноги и четыре стула расположены рядом с каждым столом. Ноги столов и стульев распространены. Сколько детей может сидеть в кондитерских, если каждый ребенок сидит на одном стуле? Решение. Из условия, что каждая таблица имеет 4 стула с тремя ногами.
Поэтому четверо детей сидят на одном столе. Ножки вокруг стола 4 3 =. Задача. У одного фермера есть куры и кролики. Число голов всех животных составляет 60, а число их ног -. Куры и кролики - 60, а 4 - 160. . Тогда у кур есть 80 штук. Задача Мими и Лили собрали тройные и четырехместные клеверы.
Примеры для самостоятельного решения. Решите уравнения: 9х³ - 18х = х – 2, х ³ - х ² = х – 1, х ³ - 3х² -3х + 1 = 0, Х ⁴ - 2х³ + 2х – 1 = 0, Х⁴ - 3х² + 2 = 0, х ⁵ + 5х³ - 6х² = 0, х ³ + 4х² + 5х + 2 = 0, Х⁴ + 4х³ - х ² - 16х – 12 = 0 4х³ + х ² - х + 5 = 0 3х⁴ + 5х³ - 9х² - 9х + 10 = 0. Ответы: 1) ±1/3; 2 2) ±1, 3) -1; 2 ±√3 , 4) ±1, 5) ± 1; ±√2 , 6) 0; 1 7) -2; -1, 8) -3; -1; ±2, 9) – 5/4 10) -2; - 5/3; 1.
Уравнения вида (х + а)(х + в)(х + с)(х + d)… = А. Пример №3 . Решите уравнение (х + 1)(х + 2)(х + 3)(х + 4) =24. а = 1, в = 2, с = 3, d = 4 а + d = в + с. Перемножаем первую скобку с четвертой и вторую с третьей. (х + 1)(х + 4)(х + 20(х + 3) = 24. (х ² + 5х + 4)(х ² + 5х + 6) = 24. Пусть х ² + 5х + 4 = у, тогда у(у + 2) = 24, у² + 2у – 24 = 0 у₁ = - 6, у₂ = 4. х ² + 5х + 4 = -6 или х ² + 5х + 4 = 4. х ² + 5х + 10 = 0, Д
Найдено 123 клевера с общим количеством 370 листов. Сколько четырехлистников было у девочек? Тройной и четырехъядерный - 123. 3. тройной и 4. четырехугольник - все листы - 370. Количество голов всех животных составляет 30, а количество их голов -. Сколько кур и сколько кроликов делает фермер?
При условии, что кур и кроликов всего 30. Если куры и кролики составляют 80 человек. Из условия заключаем, что. Куры и кролики - всего 40. Годы кака не более 9, тогда мои 5. Если число треугольников и прямоугольников равно 16, а число всех их углов равно 57, найдите количество прямоугольников?
Примеры для самостоятельного решения. (х + 1)(х + 3)(х + 5)(х + 7) = -15, х (х + 4)(х + 5)(х + 9) + 96 = 0, х (х + 3)(х + 5)(х + 8) + 56 = 0, (х – 4)(х – 3)(х – 2)(х – 1) = 24, (х – 3)(х -4)(х – 5)(х – 6) = 1680, (х ² - 5х)(х + 3)(х – 8) + 108 = 0, (х + 4)² (х + 10)(х – 2) + 243 = 0 (х ² + 3х + 2)(х ² + 9х + 20) = 4, Указание: х + 3х + 2 = (х + 1)(х + 2), х ² + 9х + 20 = (х + 4)(х + 5) Ответы: 1) -4 ±√6; - 6; - 2. 6) - 1; 6; (5± √97)/2 7) -7; -1; -4 ±√3.
Возвратные уравнения. Определение №1. Уравнение вида: ах⁴ + вх ³ + сх ² + вх + а = 0 называется возвратным уравнением четвертой степени. Определение №2. Уравнение вида: ах⁴ + вх ³ + сх ² + квх + к² а = 0 называется обобщенным возвратным уравнением четвертой степени. к² а: а = к² ; кв: в = к. Пример №6. Решите уравнение х ⁴ - 7х³ + 14х² - 7х + 1 = 0. Делим обе части уравнения на х ² . х ² - 7х + 14 – 7/ х + 1/ х ² = 0, (х ² + 1/ х ²) – 7(х + 1/ х) + 14 = 0. Пусть х + 1/ х = у. Возводим обе части равенства в квадрат. х ² + 2 + 1/ х ² = у² , х ² + 1/ х ² = у² - 2. Получаем квадратное уравнение у² - 7у + 12 = 0, у₁ = 3, у₂ = 4. х + 1/ х =3 или х + 1/ х = 4. Получаем два уравнения: х ² - 3х + 1 = 0, х ² - 4х + 1 = 0. Пример №7. 3х⁴ - 2х³ - 31х² + 10х + 75 = 0. 75:3 = 25, 10:(– 2) = -5, (-5)² = 25. Условие обобщенного возвратного уравнения выполняется к= -5. Решается аналогично примеру №6. Делим обе части уравнения на х ². 3х⁴ - 2х – 31 + 10/ х + 75/ х ² = 0, 3(х ⁴ + 25/ х ²) – 2(х – 5/ х) – 31 = 0. Пусть х – 5/ х = у, возводим обе части равенства в квадрат х ² - 10 + 25/ х ² = у² , х ² + 25/ х ² = у² + 10. Имеем квадратное уравнение 3у² - 2у – 1 = 0, у₁ = 1, у₂ = - 1/3. х – 5/ х = 1 или х – 5/ х = -1/3. Получаем два уравнения: х ² - х – 5 = 0 и 3х² + х – 15 = 0
Задача На рождественском конкурсе участвуют 48 студентов третьего класса. Все номера разделены поровну. В каждой комнате шесть мальчиков. Сколько комнат выделяется студентам, если девочки меньше мальчиков? Если они находятся в одной комнате, мальчикам - 6, а девочки 42.
Если в комнате 7 комнат, мальчиков 6 = 42, девочек 8, и их невозможно разделить на 7 комнат. Несколько рыбаков поймали 9 рыб и несколько рыб на реке. Сколько рыбаков поймали 9 рыб? Если рыбак поймал 9 рыб, остальные должны были поймать 50-9 = 41 рыба.
Если пять рыбаков поймали 9 рыб, остальные должны были поймать 50-9 = 50-45 = 5 рыб - невозможно. Таким образом, 4 рыбака поймали 9 рыб. В соревнованиях по математике участвовали две команды с таким же количеством участников. Они набрали в общей сложности 67 очков.
Примеры для самостоятельного решения. 1. 78х⁴ - 133х³ + 78х² - 133х + 78 = 0, 2. х ⁴ - 5х³ + 10х² - 10х + 4 = 0, 3. х ⁴ - х ³ - 10х² + 2х + 4 = 0, 4. 6х⁴ + 5х³ - 38х² -10х + 24 = 0, 5. х ⁴ + 2х³ - 11х² + 4х + 4 = 0, 6. х ⁴ - 5х³ + 10х² -10х + 4 = 0. Ответы: 1) 2/3; 3/2, 2) 1;2 3) -1 ±√3; (3±√17)/2, 4) -1±√3; (7±√337)/12 5) 1; 2; (-5± √17)/2, 6) 1; 2.
Однородные уравнения. Определение. Уравнение вида а₀ u³ + а₁ u² v + а₂ uv² + а₃ v³ = 0 называется однородным уравнением третьей степени относительно u v . Определение. Уравнение вида а₀ u⁴ + а₁ u³v + а₂ u²v² + а₃ uv³ + а₄ v⁴ = 0 называется однородным уравнением четвертой степени относительно u v . Пример №8. Решите уравнение (х ² - х + 1)³ + 2х⁴(х ² - х + 1) – 3х⁶ = 0 Однородное уравнение третьей степени относительно u = х ²- х + 1, v = х ². Делим обе части уравнения на х ⁶. Предварительно проверили, что х = 0 не является корнем уравнения. (х ² - х + 1/ х ²)³ + 2(х ² - х + 1/ х ²) – 3 = 0. (х ² - х + 1)/ х ²) = у, у³ + 2у – 3 = 0, у = 1 корень уравнения. Делим многочлен Р(х) = у³ + 2у – 3 на у – 1 по схеме Горнера. В частном получаем трехчлен, который не имеет корней. Ответ: 1.
Найдите общее количество участников, если каждый из них имеет 3 или 8 очков. Мы можем найти ответ, проверив, но мы можем найти его с логическими рассуждениями. Число всех спортсменов - четное число, потому что у групп одинаковое количество участников.
Из всех вариантов 3 - 3, 27 и 51. Тогда дети, получившие 3 балла, могут быть 1, 9 или 17. Затем дети получили 8 очков соответственно: 8, 5 или 4. В этой задаче и во многих других текстовых задачах более целесообразно упорядочить наше рассуждение как уравнение с двумя неизвестными.
Прямоугольник и квадрат имеют один и тот же периметр шириной 12 см и смежны друг с другом. Если их стороны являются натуральными числами, окружность фигуры. Задача В коробке есть 100 граммов конфет и шоколадных конфет с лимонными нотами больше, чем конфеты. Каждый лимонный омар весит 5 граммов, а каждый шоколад - 7 грамм.
Примеры для самостоятельного решения. 1. 2(х ² + 6х + 1)² + 5(Х² + 6Х + 1)(Х² + 1) + 2(Х² + 1)² = 0, 2. (Х + 5)⁴ - 13Х²(Х + 5)² + 36Х⁴ = 0, 3. 2(Х² + Х + 1)² - 7(Х – 1)² = 13(Х³ - 1), 4. 2(Х -1)⁴ - 5(Х² - 3Х + 2)² + 2(х – 2)⁴ = 0, 5. (х ² + х + 4)² + 3х(х ² + х + 4) + 2х² = 0, Ответы: 1) -1; -2±√3, 2) -5/3; -5/4; 5/2; 5 3) -1; -1/2; 2;4 4) ±√2; 3±√2, 5) Корней нет.
Метод неопределенных коэффициентов. Теорема №3. Два многочлена Р(х) и G(х) тождественны тогда и только тогда, когда они имеют одинаковую степень и коэффициенты при одноименных степенях переменной в обоих многочленах равны. Пример №9. Разложить на множители многочлен у⁴ - 4у³ + 5у² - 4у + 1. у⁴ - 4у³ + 5у² - 4у + 1 = (у² + ву + с)(у² + в₁у + с₁) =у ⁴ +у³(в₁ + в) + у²(с₁ + с + в₁в) + у(вс ₁ + св ₁) + сс ₁. Согласно теореме №3 имеем систему уравнений: в₁ + в = -4, с₁ + с + в₁в = 5, вс ₁ + св ₁ = -4, сс ₁ = 1. Необходимо решить систему в целых числах. Последнее уравнение в целых числах может иметь решения: с = 1, с₁ =1; с = -1, с₁ = -1. Пусть с = с ₁ = 1, тогда из первого уравнения имеем в₁ = -4 –в. Подставляем во второе уравнение системы в² + 4в + 3 = 0, в = -1, в₁ = -3 или в = -3, в₁ = -1. Данные значения подходят третьему уравнению системы. При с = с ₁ = -1 Д
Задача В клубе была задача купить трикотажные трикотажные изделия для баскетбольной команды клуба. В магазине продаются два вида трикотажных изделий - 8 левов и 9 левов. Сколько трикотажных изделий может купить покупатель, если у него 144 лева, и он должен все потратить?
Задача Длина и ширина в сантиметрах прямоугольника являются натуральными числами. Лицо прямоугольника составляет 12 квадратных сантиметров. Какая наименьшая окружность этого прямоугольника? Задание Пять художников нарисовали 100 картин. Первый нарисовал второй и третий вместе, второй - 2 раза четвертый. Третий окрашивал столько же, сколько пяткой. Если четвертый нарисовал больше пятого, то сколько картин рисовал четвертый художник.
Пример №10. Разложить на множители многочлен у³ - 5у + 2. у³ -5у + 2 = (у + а)(у² + ву + с) = у³ + (а + в)у² + (ав +с)у + ас. Имеем систему уравнений: а + в = 0, ав + с = -5, ас = 2. Возможные целые решения третьего уравнения: (2; 1), (1; 2), (-2; -1), (-1; -2). Пусть а = -2, с = -1. Из первого уравнения системы в = 2, что удовлетворяет второму уравнению. Подставляя данные значения в искомое равенство получим ответ: (у – 2)(у² + 2у – 1). Второй способ. У³ - 5у + 2 = у³ -5у + 10 – 8 = (у³ - 8) – 5(у – 2) = (у – 2)(у² + 2у -1).
Задача В футбольной игре победитель выигрывает 3 очка, а проигравший набирает 0 очков. Если оценка равна, обе команды в одной точке. Найдите наибольшую потерю для этой команды? Первый способ Если вы проиграете 12, есть 26 матчей с 80 очками, это не возможный результат, потому что, даже если вы выиграете 26, они носят 3 = 78 очков.
Если вы проиграете 11, 27 матчей с 80 очками тоже не будут возможны. Прямое тестирование теста началось с максимально возможных потерь, поэтому они. Поэтому для этой команды ничьи верны. Тест состоит из 40 задач, которые несут 1, 2 или 3 точки. Максимальное количество точек, которые вы можете получить, - это максимальное количество трехточечных задач, если тест содержит задания из всех трех?
Примеры для самостоятельного решения. Разложите на множители многочлены: 1. у⁴ + 4у³ + 6у² +4у -8, 2. у⁴ - 4у³ + 7у² - 6у + 2, 3. х ⁴ + 324, 4. у⁴ -8у³ + 24у² -32у + 15, 5. Решите уравнение, используя метод разложения на множители: а) х ⁴ -3х² + 2 = 0, б) х ⁵ +5х³ -6х² = 0. Ответы: 1) (у² +2у -2)(у² +2у +4), 2) (у – 1)²(у² -2у + 2), 3) (х ² -6х + 18)(х ² + 6х + 18), 4) (у – 1)(у – 3)(у² -4у + 5), 5а) ± 1; ±√2 , 5б) 0; 1.
Задача На столе есть пластиковые треугольники и квадрациклы. Число цифр равно 12, и на всех пиках. Первый путь Из того, что общее число равно 12, в три раза общее число. С другой стороны, мы знаем, что общее число всех пиков равно 43. Так как треугольник имеет три вершины, а четырехугольник с еще одним, разность 43-36 = 7 - это точно число всех четырехугольников.
Если треугольники равны х и квадрациклы верны, то уравнения будут правильными. Возраст бабушки Марины - это двузначное число, первое - возраст одной внучки, а второй - возраст другой внучки. Найдите, сколько лет Бабушке Марине, если младшей внучке 5 лет, а сумма трех лет.
Функционально – графический метод решения уравнений высших степеней. Пример №11. Решите уравнение х ⁵ + 5х -42 = 0. Функция у = х ⁵ возрастающая, функция у = 42 – 5х убывающая (к
Примеры для самостоятельного решения. 1. Используя свойство монотонности функции, докажите, что уравнение имеет единственный корень, и найдите этот корень: а) х ³ = 10 – х, б) х ⁵ + 3х³ - 11√2 – х. Ответы: а) 2, б) √2. 2. Решите уравнение, используя функционально – графический метод: а) х = ³ √х, б) l х l = ⁵ √х, в) 2 = 6 – х, г) (1/3) = х +4, д) (х – 1)² = log₂ х, е) log = (х + ½)² , ж) 1 - √х = ln х, з) √х – 2 = 9/х. Ответы: а) 0; ±1, б) 0; 1, в) 2, г) -1, д) 1; 2, е) ½, ж) 1, з) 9.
Решение внукам внучки бабушки должно быть лет, а затем бабушке Марине будет 10 лет. Если разрыв рождаемости в два раза меньше суммы дат рождения Веси, найдите день рождения Веси. В ячейках квадрата размером от 5 до 5 записаны натуральные числа, сумма которых представляет собой сумму чисел в каждых двух смежных квадратах, является тем же самым нечетным числом.
Каковы цифры, написанные? Задача В одной коробке есть 50 мячей, каждый из которых окрашен в белый, зеленый или красный. Количество белых в 11 раз превышает количество зелени. Коробка менее красная, чем белая, но более красная, чем зеленые шары. Сколько красных меньше белого?
Формулы Виета для уравнений высших степеней. Теорема №5 (Теореме Виета). Если уравнение а х ⁿ + а х ⁿ + … + а₁х + а₀ имеет n различных действительных корней х ₁, х ₂, … , х, то они удовлетворяют равенствам: Для квадратного уравнения ах² + вх + с = о: х ₁ + х ₂ = -в/а, х₁х ₂ = с/а; Для кубического уравнения а₃х ³ + а₂х ² + а₁х + а₀ = о: х ₁ + х ₂ + х ₃ = -а₂/а₃; х₁х ₂ + х₁х ₃ + х₂х ₃ = а₁/а₃; х₁х₂х ₃ = -а₀/а₃; …, для уравнения n –ой степени: х ₁ + х ₂ + … х = - а / а, х₁х ₂ + х₁х ₃ + … + х х = а / а, … , х₁х ₂·… · х = (- 1) ⁿ а₀/а. Выполняется и обратная теорема.
Тогда шары в цветах будут. Из и следует, что количество зелени может быть только 3. Задача В бальном зале есть два вида украшенных новогодних деревьев. На елях первого рода есть в 2 раза больше игрушек, чем другие елки. В общей сложности 11 таких деревьев имеют столько же игрушек, сколько 6 игрушек первого типа и 6 игрушек второго рода. Сколько деревьев из них 11 первого типа?
Задача Сумма трех разных двухзначных положительных чисел Найдите разницу между наибольшим и наименьшим, если один делится на 11, один делится на 7, а два делятся на. Первый случай суммы трех чисел. Число заканчивается на 0 или 5. Второй случай суммы трех чисел.
Пример №13. Напишите кубическое уравнение, корни которого обратны корням уравнения х ³ - 6х² + 12х – 18 = 0, а коэффициент при х ³ равен 2. 1. По теореме Виета для кубического уравнения имеем: х ₁ + х ₂ + х ₃ = 6, х₁х ₂ + х₁х ₃ + х₂х ₃ = 12, х₁х₂х ₃ = 18. 2. Составляем обратные величины данным корням и для них применяем обратную теорему Виета. 1/ х ₁ + 1/ х ₂ + 1/ х ₃ = (х₂х ₃ + х₁х ₃ + х₁х ₂)/ х₁х₂х ₃ = 12/18 = 2/3. 1/ х₁х ₂ + 1/ х₁х ₃ + 1/ х₂х ₃ = (х ₃ + х ₂ + х ₁)/ х₁х₂х ₃ = 6/18 = 1/3, 1/ х₁х₂х ₃ = 1/18. Получаем уравнение х ³ +2/3х² + 1/3х – 1/18 = 0 · 2 Ответ: 2х³ + 4/3х² + 2/3х -1/9 = 0.
Ищет количество двух или более неизвестных элементов с общей функцией. Существует логическая тонкость при изучении всех вариантов, и часто студенты делают ошибки. Многие текстовые задачи имеют именно такие уравнения для математической модели. При решении диофантовых уравнений мы будем использовать наши знания о делимости чисел, мы будем оценивать наибольшее или наименьшее значение, которое могут иметь неизвестные, разлагаться на простые множители, сузить область принятия решения в соответствии с условием задачи только со знанием с курса математической школы.
Примеры для самостоятельного решения. 1. Напишите кубическое уравнение, корни которого обратны квадратам корней уравнения х ³ - 6х² + 11х – 6 = 0, а коэффициент при х ³ равен 8. Ответ: 8х³ - 98/9х² + 28/9х -2/9 = 0. Нестандартные методы решений уравнений высших степеней. Пример №12. Решите уравнение х ⁴ -8х + 63 = 0. Разложим левую часть уравнения на множители. Выделим точные квадраты. Х⁴ - 8х + 63 = (х ⁴ + 16х² + 64) – (16х² + 8х + 1) = (х ² + 8)² - (4х + 1)² = (х ² + 4х + 9)(х ² - 4х + 7) = 0. Оба дискриминанта отрицательные. Ответ: нет корней.
Страница с решенными задачами и примерами самозанятых работ предлагает сложные примеры для сложных задач. Элемент находится в каждом соревновании по математике для всех классов. Для студентов второго и третьего классов мы предлагаем систему задач и примеров из самых популярных математических математических соревнований, проводимых в Болгарии, и методов их решения без уравнений.
Дифференциальное уравнение представляет собой математическое описание дома, которое непрерывно меняется в зависимости от другого свойства, скажем, например. на расстоянии или примерно на некотором расстоянии от определенной точки. Разница - это разновидность различий между функциональными значениями рассматриваемой функции в двух соседних точках. Если мы представляем движение момента во времени, это фактически скорость, с которой точка переходит из одного места в другое в течение определенного периода времени.
Пример №14. Решите уравнение 21х³ + х ² - 5х – 1 = 0. Если свободный член уравнения равен ± 1, то уравнение преобразуется в приведенное уравнение с помощью замены х = 1/у. 21/у³ + 1/у² - 5/у – 1 = 0 · у³, у³ + 5у² -у – 21 = 0. у = -3 корень уравнения. (у + 3)(у² + 2у -7) = 0, у = -1 ± 2√2. х ₁ = -1/3, х ₂ = 1/ -1 + 2√2 = (2√2 + 1)/7, Х₃ = 1/-1 -2√2 =(1-2√2)/7. Пример №15. Решите уравнение 4х³-10х² + 14х – 5 = 0. Умножим обе части уравнения на 2. 8х³ -20х² + 28х – 10 = 0, (2х)³ - 5(2х)² + 14·(2х) -10 = 0. Введем новую переменную у = 2х, получим приведенное уравнение у³ - 5у² + 14у -10 = 0, у = 1 корень уравнения. (у – 1)(у² - 4у + 10) = 0, Д
Пример №16. Доказать, что уравнение х ⁴ + х ³ + х – 2 = 0 имеет один положительный корень. Пусть f (х) = х ⁴ + х ³ + х – 2, f’ (х) = 4х³ + 3х² + 1 > о при х > о. Функция f (х) возрастающая при х > о, а значение f (о) = -2. Очевидно, что уравнение имеет один положительный корень ч.т.д. Пример №17. Решите уравнение 8х(2х² - 1)(8х⁴ - 8х² + 1) = 1. И.Ф.Шарыгин « Факультативный курс по математике для 11 класса».М. Просвещение 1991 стр90. 1. l х l 1 2х² - 1 > 1 и 8х⁴ -8х² + 1 > 1 2. Сделаем замену х = cosy , у € (0; п). При остальных значениях у, значения х повторяются, а уравнение имеет не более 7 корней. 2х² - 1 = 2 cos²y – 1 = cos2y , 8х⁴ - 8х² + 1 = 2(2х² - 1)² - 1 = 2 cos²2y – 1 = cos4y . 3. Уравнение принимает вид 8 cosycos2ycos4y = 1. Умножаем обе части уравнения на siny . 8 sinycosycos2ycos4y = siny . Применяя 3 раза формулу двойного угла получим уравнение sin8y = siny , sin8y – siny = 0
Окончание решения примера №17. Применяем формулу разности синусов. 2 sin7y/2 · cos9y/2 = 0 . Учитывая, что у € (0;п), у = 2пк/3, к = 1, 2, 3 или у = п /9 + 2пк/9, к =0, 1, 2, 3. Возвращаясь к переменной х получаем ответ: Cos2 п /7, cos4 п /7, cos6 п /7, cos п /9, ½, cos5 п /9, cos7 п /9 . Примеры для самостоятельного решения. Найти все значения а, при которых уравнение (х ² + х)(х ² + 5х + 6) = а имеет ровно три корня. Ответ: 9/16. Указание: построить график левой части уравнения. F max = f(0) = 9/16 . Прямая у = 9/16 пересекает график функции в трех точках. Решите уравнение (х ² + 2х)² - (х + 1)² = 55. Ответ: -4; 2. Решите уравнение (х + 3)⁴ + (х + 5)⁴ = 16. Ответ: -5; -3. Решите уравнение 2(х ² + х + 1)² -7(х – 1)² = 13(х ³ - 1).Ответ: -1; -1/2, 2;4 Найдите число действительных корней уравнения х ³ - 12х + 10 = 0 на [-3; 3/2]. Указание: найти производную и исследовать на монот.
Примеры для самостоятельного решения (продолжение). 6. Найдите число действительных корней уравнения х ⁴ - 2х³ + 3/2 = 0. Ответ: 2 7. Пусть х ₁, х ₂, х ₃ - корни многочлена Р(х) = х ³ - 6х² -15х + 1. Найдите Х₁² + х ₂² + х ₃². Ответ: 66. Указание: примените теорему Виета. 8. Докажите, что при а > о и произвольном вещественном в уравнение х ³ + ах + в = о имеет только один вещественный корень. Указание: проведите доказательство от противного. Примените теорему Виета. 9. Решите уравнение 2(х ² + 2)² = 9(х ³ + 1). Ответ: ½; 1; (3 ± √13)/2. Указание: приведите уравнение к однородному, используя равенства Х² + 2 = х + 1 + х ² - х + 1, х ³ + 1 = (х + 1)(х ² - х + 1). 10. Решите систему уравнений х + у = х ², 3у – х = у². Ответ: (0;0),(2;2), (√2; 2 - √2), (- √2 ; 2 + √2). 11. Решите систему: 4у² -3ху = 2х –у, 5х² - 3у² = 4х – 2у. Ответ: (о;о), (1;1),(297/265; - 27/53).
Контрольная работа. 1 вариант. 1. Решите уравнение (х ² + х) – 8(х ² + х) + 12 = 0. 2. Решите уравнение (х + 1)(х + 3)(х + 5)(х + 7) = - 15. 3. Решите уравнение 12х²(х – 3) + 64(х – 3)² = х ⁴. 4. Решите уравнение х ⁴ - 4х³ + 5х² - 4х + 1 = 0 5. Решите систему аравнений: х ² + 2у² - х + 2у = 6, 1,5х² + 3у² - х + 5у = 12.
2 вариант 1. (х ² - 4х)² + 7(х ² - 4х) + 12 = 0. 2. х (х + 1)(х + 5)(х + 6) = 24. 3. х ⁴ + 18(х + 4)² = 11х²(х + 4). 4. х ⁴ - 5х³ + 6х² - 5х + 1 = 0. 5. х ² - 2ху + у² + 2х²у – 9 = 0, х – у – х²у + 3 = 0. 3 вариант. 1. (х ² + 3х)² - 14(х ² + 3х) + 40 = 0 2. (х – 5)(х-3)(х + 3)(х + 1) = - 35. 3. х4 + 8х²(х + 2) = 9(х+ 2)². 4. х ⁴ - 7х³ + 14х² - 7х + 1 = 0. 5. х + у + х ² + у ² = 18, ху + х ² + у² = 19.
4 вариант. (х ² - 2х)² - 11(х ² - 2х) + 24 = о. (х -7)(х-4)(х-2)(х + 1) = -36. Х⁴ + 3(х -6)² = 4х²(6 – х). Х⁴ - 6х³ + 7х² - 6х + 1 = 0. Х² + 3ху + у² = - 1, 2х² - 3ху – 3у² = - 4. Дополнительное задание: Остаток от деления многочлена Р(х) на (х – 1) равен 4, остаток от делении на (х + 1) равен2, а при делении на (х – 2) равен 8. Найти остаток от деления Р(х) на (х ³ - 2х² - х + 2).
Ответы и указания: вариант № 1 № 2. № 3. № 4. № 5. 1. - 3; ±2; 1 1;2;3. -5; -4; 1; 2. Однородное уравнение: u = x -3, v =x² -2 ; -1; 3; 4. (2;1); (2/3;4/3). Указание: 1·(-3) + 2· 2 2. -6; -2; -4±√6. -3±2√3; - 4; - 2. 1±√11; 4; - 2. Однородное уравнение: u = x + 4, v = x² 1 ; 5;3±√13. (2;1); (0;3); (- 3; 0). Указание: 2· 2 + 1. 3. -6; 2; 4; 12 -3; -2; 4; 12 -6; -3; -1; 2. Однородное u = x+ 2, v = x² -6 ; ±3; 2 (2;3), (3;2), (-2 + √7; -2 - √7); (-2 - √7; -2 + √7). Указание: 2 -1. 4. (3±√5)/2 2±√3 2±√3; (3±√5)/2 (5 ± √21)/2 (1;-2), (-1;2). Указание: 1·4 + 2 .
Решение дополнительного задания. По теореме Безу: Р(1) = 4, Р(-1) = 2, Р(2) = 8. Р(х) = G(x) (х ³ - 2х² - х + 2) + ах² + вх + с. Подставляем 1; - 1; 2. Р(1) = G(1) ·0 + а + в + с = 4, а + в+ с = 4. Р(-1) = а – в + с = 2, Р(2) = 4а² + 2в + с = 8. Решая полученную систему из трех уравнений получим: а = в = 1, с = 2. Ответ: х ² + х + 2.
Критерий № 1 - 2 балла. 1 балл – одна вычислительная ошибка. № 2,3,4 – по 3 балла. 1 балл – привели к квадратному уравнению. 2 балла – одна вычислительная ошибка. № 5. – 4 балла. 1 балл – выразили одну переменную через другую. 2 балла – получили одно из решений. 3 балла – одна вычислительная ошибка. Дополнительное задание: 4 балла. 1 балл – применили теорему Безу для всех четырех случаев. 2 балла – составили систему уравнений. 3 балла – одна вычислительная ошибка.
При решении алгебраических уравнений часто приходится разлагать многочлен на множители. Разложить многочлен на множители – это значит представить его в виде произведения двух или нескольких многочленов. Некоторые методы разложения многочленов мы употребляем достаточно часто: вынесение общего множителя, применение формул сокращенного умножения, выделение полного квадрата, группировка. Рассмотрим ещё некоторые методы.
Иногда при разложении многочлена на множители бывают полезными следующие утверждения:
1) если многочлен, с целыми коэффициентами имеет рациональный корень (где - несократимая дробь,то -делитель свободного члена а делитель старшего коэффициента:
2) Если каким-либо образом подобрать корень многочлена степени, то многочлен можно представить в виде где многочлен степени
Многочлен можно найти либо делением многочлена на двучлен «столбиком», либо соответствующей группировку слагаемых многочлена и выделением из них множителя либо методом неопределенных коэффициентов.
Пример. Разложить на множители многочлен
Решение. Поскольку коэффициент при х4 равен 1, то рациональные корни данного многочлена, существуют, являются делителями числа 6, т. е. могут быть целыми числами ±1, ±2, ±3, ±6. Обозначим данный многочлен через Р4(х). Так как Р Р4 (1) = 4 и Р4(-4) = 23, то числа 1 и -1 не являются корнями многочлена РА{х). Поскольку Р4(2) = 0, то х = 2 является корнем многочлена Р4(х), и, значит, данный многочлен делится на двучлен х - 2. Поэтому х4 -5х3 +7х2 -5х +6 х-2 х4 -2х3 х3 -3х2 +х-3
3х3 +7х2 -5х +6
3х3 +6х2 х2 - 5х + 6 х2- 2х
Следовательно, Р4(х) = (х - 2)(х3 - Зх2 + х - 3). Так как xz - Зх2 + х - 3 = х2 (х - 3) + (х - 3) = (х - 3)(х2 + 1), то х4 - 5х3 + 7х2 - 5х + 6 = (х - 2)(х - 3)(х2 + 1).
Метод введения параметра
Иногда при разложении многочлена на множители помогает метод введения параметра. Суть этого метода поясним на следующем примере.
Пример. х3 –(√3 + 1) х2 + 3.
Решение. Рассмотрим многочлен с параметром а: х3 - (а + 1)х2 + а2, который при а = √3 превращается в заданный многочлен. Запишем этот многочлен как квадратный трехчлен относительно а: аг - ах2 + (х3 - х2).
Так как корни этого квадратного относительно а трехчлена есть а1 = х и а2 = х2 - х, то справедливо равенство а2 - ах2 + {xs - х2) = {а – х)(а - х2 + х). Следовательно, многочлен х3 - (√3 + 1)х2 + 3 разлагается на множители √3 – х и √3 - х2 + х, т. е.
х3 – (√3+1)х2+3=(х-√3)(х2-х-√3).
Метод введения новой неизвестной
В некоторых случаях путем замены выражения f{x), входящего в многочлен Рп{х), через у можно получить многочлен относительно у, который уже легко разложить на множители. Затем после замены у на f{x) получаем разложение на множители многочлена Рп{х).
Пример. Разложить на множители многочлен х(х+1)(х+2)(х+3)-15.
Решение. Преобразуем данный многочлен следующим образом: х(х+1)(х+2)(х+3)-15= [х (х + 3)][(х + 1)(х + 2)] - 15 =(х2 + 3х)(х2 + 3х + 2) - 15.
Обозначим х2 + 3х через у. Тогда имеем у(у + 2) - 15 = у2 + 2у - 15 = у2 + 2у + 1 - 16 = (у + 1)2 - 16 = (у + 1 + 4)(у + 1 - 4)= (у+ 5)(у - 3).
Поэтому х(х + 1)(х+ 2)(х + 3) - 15 = (х2+ 3х + 5)(х2 + 3х - 3).
Пример. Разложить на множители многочлен (х-4)4+(х+2)4
Решение. Обозначим х- 4+х+2 = х - 1 через у.
(х - 4)4 + (х + 2)2= (у - 3)4 + (у + 3)4 = у4 - 12у3 +54у3 - 108у + 81 + у4 + 12у3 + 54у2 + 108у + 81 =
2у4 + 108у2 + 162 = 2(у4 + 54у2 + 81) = 2[(уг + 27)2 - 648] = 2 (у2 + 27 - √б48)(у2 + 27+√б48)=
2((х-1)2+27-√б48)((х-1)2+27+√б48)=2(х2-2х + 28- 18√ 2)(x2- 2x + 28 + 18√ 2).
Комбинирование различных методов
Часто при разложении многочлена на множители приходится применять последовательно несколько из рассмотренных выше методов.
Пример. Разложить на множители многочлен х4 - 3х2 + 4х-3.
Решение. Применяя группировку, перепишем многочлен в виде x4 - 3х2 + 4х - 3 = (х4 – 2х2) – (х2 -4х + 3).
Применяя к первой скобке метод выделения полного квадрата, имеем х4 - 3х3 + 4х - 3 = (х4 - 2 ·1· х2 + 12) - (х2 -4х + 4).
Применяя формулу полного квадрата, можно теперь записать, что х4 – 3х2 + 4x - 3 = (х2 -1)2 - (х - 2)2.
Наконец, применяя формулу разности квадратов, получим, что х4 - 3х2 +4x - 3 = (х2 - 1 + х - 2)(х2 - 1 - х + 2) =(х2+х-3)(х2 -x + 1).
§ 2. Симметрические уравнения
1. Симметрические уравнения третьей степени
Уравнения вида ах3 + bх2 + bх + а = 0, а ≠ 0 (1) называются симметрическими уравнениями третьей степени. Поскольку ах3 + bх2 + bх + а = а(х3 + 1) + bх (х + 1) =(х+1)(ах2+(b-а)х+а), то уравнение (1) равносильно совокупности уравнений х + 1 = 0 и ах2 + (b-а)х + а = 0, решить которую не представляет труда.
Пример 1. Решить уравнение
3х3 + 4х2 + 4х + 3 = 0. (2)
Решение. Уравнение (2) является симметрическим уравнением третьей степени.
Поскольку 3х3 +4хг +4х + 3 = 3(х3 + 1) + 4х(х + 1) = (х+ 1)(3х2 - Зх + 3 + 4х) = (х + 1)(3х2 + х + 3), то уравнение (2) равносильно совокупности уравнений х + 1 = 0 и 3х3 + х +3=0.
Решение первого из этих уравнений есть х = -1, второе уравнение решений не имеет.
Ответ: х = -1.
2. Симметрические уравнения четвертой степени
Уравнение вида
(3) называется симметрическим уравнением четвертой степени.
Поскольку х = 0 не является корнем уравнения(3), то, разделив обе части уравнения(3) на х2, получим уравнение, равносильное исходному(3):
Перепишем уравнение (4) в виде:
В этом уравнение сделаем замену, тогда получим квадратное уравнение
Если уравнение (5) имеет 2 корня у1 и у2, то исходное уравнение равносильно совокупности уравнений
Если же уравнение (5) имеет один корень у0, то исходное уравнение равносильно уравнению
Наконец, если уравнение (5) не имеет корней, то и исходное уравнение также не имеет корней.
Пример 2. Решить уравнение
Решение. Данное уравнение является симметрическим уравнением четвертой степени. Так как х = 0 не является его корнем, то, разделив уравнение (6) на х2, получим равносильное ему уравнение:
Сгруппировав слагаемые, перепишем уравнение (7) в виде или в виде
Положив, получим уравнение имеющее два корня у1 = 2 и у2 = 3. Следовательно, исходное уравнение равносильно совокупности уравнений
Решение первого уравнения этой совокупности есть х1 = 1, а решение второго есть и.
Следовательно, исходное уравнение имеет три корня: х1, х2 и х3.
Ответ: х1=1,.
§3. Алгебраические уравнения
1. Понижение степени уравнения
Некоторые алгебраические уравнения заменой в них некоторого многочлена одной буквой могут быть сведены к алгебраическим уравнениям, степень которых меньше степени исходного уравнения и решение которых проще.
Пример 1. Решить уравнение
Решение. Обозначим через, тогда уравнение (1) можно переписать в виде Последнее уравнение имеет корни и Следовательно, уравнение (1) равносильно совокупности уравнений и. Решение первого уравнения этой совокупности есть и Решения второго уравнения есть
Решениями уравнения (1) являются
Пример 2. Решить уравнение
Решение. Умножив обе части уравнения на 12 и обозначив через,
Получим уравнение Перепишем это уравнение в виде
(3) и обозначив через перепишем уравнение (3) в виде Последнее уравнение имеет корни и Поэтому получаем, что уравнение (3) равносильно совокупности двух уравнений и Решения этой совокупности уравнений есть и т. е. уравнение (2) равносильно совокупности уравнений и (4)
Решениями совокупности (4) является и, они и являются решениями уравнения (2).
2. Уравнения вида
Уравнение
(5) где -данные числа, можно свести к биквадратному уравнению с помощью замены неизвестной т. е. замены
Пример 3. Решить уравнение
Решение. Обозначим через,т. е. сделаем замену переменных или Тогда уравнение (6) можно переписать в виде или, применяя формулу, в виде
Поскольку корни квадратного уравнения есть и то решения уравнения (7) есть решения совокупности уравнений и. Это совокупность уравнений имеет два решения и Следовательно, решения уравнения (6) есть и
3. Уравнения вида
Уравнение
(8) где числа α, β, γ, δ, и Α таковы, что α
Пример 4. Решить уравнение
Решение. Сделаем замену неизвестных т. е. y=x+3 или x = y – 3. Тогда уравнение (9) можно переписать в виде
(y-2)(y-1)(y+1)(y+2)=10, т. е. в виде
(y2- 4)(y2-1)=10(10)
Биквадратное уравнение (10) имеет два корня. Следовательно, уравнение (9) так же имеет два корня:
4. Уравнения вида
Уравнение, (11)
Где, не имеет корня x = 0, поэтому, разделив уравнение (11) на x2 , получим равносильное ему уравнение
Которое после замены неизвестной перепишется в виде квадратного уравнения, решение которого не представляет трудностей.
Пример 5. Решить уравнение
Решение. Так как ч = 0 не является корнем уравнения (12), то, разделив его на x2, получим равносильное ему уравнение
Делая замену неизвестной, получим уравнение (y+1)(y+2)=2, которое имеет два корня: y1 = 0 и y1 = -3. Следовательно, исходное уравнение (12) равносильно совокупности уравнений
Эта совокупность имеет два корня: x1= -1 и x2 = -2.
Ответ: x1= -1, x2 = -2.
Замечание. Уравнение вида,
У которого, всегда можно привести к виду (11) и, более того, считая α > 0 и λ > 0 к виду.
5. Уравнения вида
Уравнение
,(13) где числа, α, β, γ, δ, и Α таковы, что αβ = γδ ≠ 0, можно переписать, перемножив первую скобку со второй, а третью с четвертой, в виде т. е. уравнение (13) теперь записано в виде (11), и его решение можно проводить так же, как и решение уравнения (11).
Пример 6. Решить уравнение
Решение. Уравнение (14) имеет вид (13) , поэтому перепишем его в виде
Так как х = 0 не есть решение этого уравнения, то, разделив его обе части на х2, получим равносильное исходное уравнение. Делая замену переменных, получаем квадратное уравнение, решение которого есть и. Следовательно, исходное уравнение (14) равносильно совокупности уравнений и.
Решение первого уравнения этой совокупности есть
Второе уравнение этой совокупности решений не имеет. Итак, исходное уравнение имеет корни х1 и х2.
6. Уравнения вида
Уравнение
(15) где числа a, b, c, q, A таковы, что, не имеет корня х = 0, поэтому, разделив уравнение (15) на х2. получим равносильное ему уравнение, которое после замены неизвестной перепишется в виде квадратного уравнения, решение которого не представляет трудностей.
Пример 7. Решение уравнения
Решение. Так как х = 0 не является корнем уравнения (16), то, разделив обе его части на х2, получим уравнение
, (17) равносильное уравнению (16). Сделав замену неизвестной, уравнение (17) перепишем в виде
Квадратное уравнение (18) имеет 2 корня: у1 = 1 и у2 = -1. Поэтому уравнение (17) равносильно совокупности уравнений и (19)
Совокупность уравнений (19) имеет 4 корня: ,.
Они будут корнями уравнения (16).
§4. Рациональные уравнения
Уравнения вида = 0, где Н(х) и Q(x) – многочлены, называются рациональными.
Найдя корни уравнения Н(х) = 0, затем надо проверить, какие из них не являются корнями уравнения Q(x) = 0. Эти корни и только они будут решениями уравнения.
Рассмотрим некоторые методы решения уравнения вида = 0.
1. Уравнения вида
Уравнение
(1) при некоторых условиях на числа может быть решено следующим образом. Группируя члены уравнения (1) по два и суммируя каждую пару, надо получить в числителе многочлены первой или нулевой степени, отличающиеся только числовыми множителями, а в знаменателях – трехчлены с одинаковыми двумя членами, содержащими х, тогда после замены переменных получение уравнение будет либо иметь также вид (1), но с меньшим числом слагаемых, либо будет равносильно совокупности двух уравнений, одно из которых будет первой степени, а второе будет уравнением вида (1), но с меньшим числом слагаемых.
Пример. Решить уравнение
Решение. Сгруппировав в левой части уравнения (2) первый член с последним, а второй с предпоследним, перепишем уравнение (2) в виде
Суммируя в каждой скобке слагаемые, перепишем уравнение (3) в виде
Так как не есть решение уравнения (4), то, разделив это уравнение на, получим уравнение
, (5) равносильное уравнению (4). Сделаем замену неизвестного, тогда уравнение (5) перепишется в виде
Таким образом, решение уравнения (2) с пятью слагаемыми в левой части сведено к решению уравнения (6) того же вида, но с тремя слагаемыми в левой части. Суммируя все члены в левой части уравнения (6), перепишем его в виде
Решения уравнения есть и. Ни одно из этих чисел не обращает в нуль знаменатель рациональной функции в левой части уравнения (7). Следовательно, уравнение (7) имеет эти два корня, и поэтому исходное уравнение (2) равносильно совокупности уравнений
Решения первого уравнения этой совокупности есть
Решения второго уравнения из этой совокупности есть
Поэтому исходное уравнение имеет корни
2. Уравнения вида
Уравнение
(8) при некоторых условиях на числа можно решить так: надо выделить целую часть в каждой из дробей уравнения, т. е. заменить уравнение (8) уравнением
Свести его к виду (1) и затем решить его способом, описанным в предыдущем пункте.
Пример. Решить уравнение
Решение. Запишем уравнение (9) в виде или в виде
Суммируя слагаемые в скобках, перепишем уравнение (10) в виде
Делая замену неизвестного, перепишем уравнение (11) в виде
Суммируя члены в левой части уравнения (12), перепишем его в виде
Легко видеть, что уравнение (13) имеет два корня: и. Следовательно, исходное уравнение (9) имеет четыре корня:
3) Уравнения вида.
Уравнение вида (14) при некоторых условиях на числа можно решать так: разложив (если это, конечно, возможно) каждую из дробей в левой части уравнения (14) в суму простейших дробей
Свести уравнение (14) к виду (1), затем, проведя удобную перегруппировку членов полученного уравнения, решать его методом, изложенном в пункте 1).
Пример. Решить уравнение
Решение. Поскольку и, то, умножив числитель каждой дроби в уравнении (15) на 2 и заметив, что уравнение (15) можно записать в виде
Уравнение (16) имеет вид (7). Перегруппировав слагаемые в этом уравнении, перепишем его в виде или в виде
Уравнение (17) равносильно совокупности уравнений и
Для решения второго уравнения совокупности (18) сделаем замену неизвестного Тогда оно перепишется в виде или в виде
Суммируя все члены в левой части уравнения (19),перепишите его в виде
Так как уравнение не имеет корней, то уравнение (20) их также не имеет.
Первое уравнение совокупности (18) имеет единственный корень Поскольку этот корень входит в ОДЗ второго уравнения совокупности (18), то он является единственным корнем совокупности (18), а значит, и исходного уравнения.
4. Уравнения вида
Уравнение
(21) при некоторых условиях на числа и A после представления каждого слагаемого в левой части в виде может быть сведено к виду (1).
Пример. Решить уравнение
Решение. Перепишем уравнение (22) в виде или в виде
Таким образом, уравнение (23) сведено к виду (1). Теперь, группируя первый член с последним, а второй с третьим, перепишем уравнение (23) в виде
Это уравнение равносильно совокупности уравнений и. (24)
Последнее уравнение совокупности (24) можно переписать в виде
Решения этого уравнения есть и, так как входит в ОДЗ второго уравнения совокупности (30), то совокупность (24) имеет три корня:. Все они есть решения исходного уравнения.
5. Уравнения вида.
Уравнение вида (25)
При некоторых условиях на числа заменой неизвестного можно свести к уравнению вида
Пример. Решить уравнение
Решение. Так как не является решением уравнения (26), то разделив числитель и знаменатель каждой дроби в левой части на, перепишем его в виде
Сделав замену переменных перепишем уравнение (27) в виде
Решая уравнение (28) есть и. Поэтому уравнение (27) равносильно совокупности уравнений и. (29)
- Митрополит алексий московский святитель и чудотворец краткая биография Митрополит алексий годы
- Попробуем разобраться в см - Документ
- Открытия галилея в области астрономии
- Сопливые грибы но не маслята
- Имена мальчиков рожденных в январе Азербайджанские имена родившиеся в январе по гороскопу
- Суточный диурез у беременных женщин
- Как рассчитать налог на автомобиль по лошадиным силам Изменения по транспортному налогу в году

 Live Journal
Live Journal Facebook
Facebook Twitter
Twitter