В чем заключается неравенство треугольника. Неравенство треугольника. Полные уроки — Гипермаркет знаний. Историческая справка о признаках равенства треугольников
Математический кружок Русановского лицея
Неравенство треугольника
Неравенство треугольника – один из важнейших геометрических фактов. Представляя собой одно из интуитивных свойств расстояния, оно нередко помогает в решении непростых геометрических и текстовых задач. С помощью неравенства треугольника представляется возможным отсеять часть из возможных вариантов расположения каких-либо элементов в громоздких геометрических задачах. Часто именно невыполнение строгого неравенства треугольника (а именно – достижение в нем равенства) дает основание утверждать о принадлежности трех точек одной прямой. Таким образом, неравенство треугольника является одновременно интуитивно понятным, даже очевидным, но весьма часто становится мощным инструментом при решении серьезных математических задач.
Может ли треугольник быть сформирован с любыми тремя сторонами длины? Захватите 3 карандаша или ручки различной длины. Можете ли вы поместить их в конец, чтобы сформировать треугольник? На рисунке выше треугольник может быть сформирован с тремя карандашами. Что делать, если у вас есть два действительно коротких карандаша и один длинный карандаш? Будут ли два коротких всегда иметь возможность достичь треугольника?
На рисунке выше вы можете видеть, что два коротких карандаша не достаточно длинны, чтобы образовать треугольник. Бывают случаи, когда треугольник не может быть сформирован с тремя заданными сторонами длины. Иногда две кратчайшие стороны не были достаточно длинными, чтобы касаться друг друга, чтобы сформировать треугольник.
Несколько слов о неравенствах
В математике неравенство есть утверждение об относительной величине или порядке двух рассматриваемых объектов или о том, что они просто не одинаковы. Классическое неравенство как объект исследования можно также рассматривать как частный случай отношения порядка. Различают строгие и нестрогие неравенства. Или же, переходя на язык отношений, строгое неравенство можно считать отношением строгого порядка на множестве действительных чисел (то есть отношением, которое обладает свойствами антирефлексивности, антисимметричности и транзитивности). Если же речь идет о нестрогом неравенстве, то можно говорить о нем как об отношении нестрогого порядка на том же множестве (то есть рассматривать вместо антирефлексивности рефлексивность). Напомним, что об отношениях как математическом объекте и их свойствах мы уже упоминали в Лекции 7 (были рассмотрены свойства отношения делимости). Более подробное их изучение нам предстоит в будущем, поскольку они довольно успешно систематизируют и обобщают ряд элементарных математических понятий. Теперь же мы приведем несколько примеров неравенств каждого из названных типов. Строгими неравенствами называют такие неравенства:
Итак, как мы узнаем, могут ли три заданные стороны длины образовывать треугольник? Если вам даны три длины сторон, представьте, что два самых коротких из них поставлены от конца до конца, а самая длинная сторона расположена прямо под ними. Если два коротких вместе взятых длиннее самой длинной стороны, они смогут сгибаться до образуют треугольник.
Если вы поместите две самые короткие стороны в конец и они не будут длиннее самой длинной стороны, они не смогут достичь, когда вы попытаетесь сформировать треугольник. Что, если вы положите два коротких конца в конец, и они «точно соответствуют длине самой длинной стороны?» Чтобы «вырваться», чтобы сформировать треугольник, должна быть небольшая дополнительная комната. Если они «просто» касаясь концов самой длинной стороны, когда они параллельны самой длинной стороне, там нет места для их уклонения и формирования треугольника.
- a
< b
– означает, что a
меньше
b
; a
> b
– означает, что a
больше
b
; a
≠ b
– означает, что a
не равно
b
или же что a
и b
различны
.
- a
≤ b
– означает, что a
меньше либо равно
b
или, что то же самое, a
не больше (не превосходит, не превышает)
b
; a
≥
b
– означает, что a
больше либо равно
b
или, что то же самое, a
не меньше
b
.
Неравенство треугольника
Теорема о неравенстве треугольника
Две самые короткие стороны, поставленные от конца до конца, должны быть длиннее самой длинной. Если бы вы попытались поставить два самых коротких из них под углом, они были бы очень близки к формированию треугольника, но не достаточно долго. Теорема о неравенстве треугольника - это более формальный способ описать то, что мы обнаружили на предыдущей вкладке. Мы обнаружили, что когда вы ставите две короткие стороны в конец, они должны быть длиннее самой длинной.
Это всего лишь один из способов сформулировать теорему о неравенстве треугольника. Другой способ заявить, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Сначала определите две кратчайшие стороны: 4 и если вы найдете сумму двух кратчайших сторон, то она больше самой длинной?
|
|
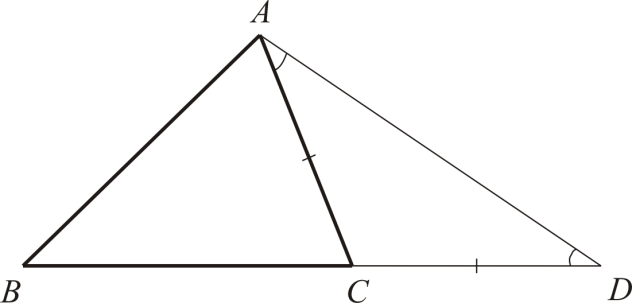
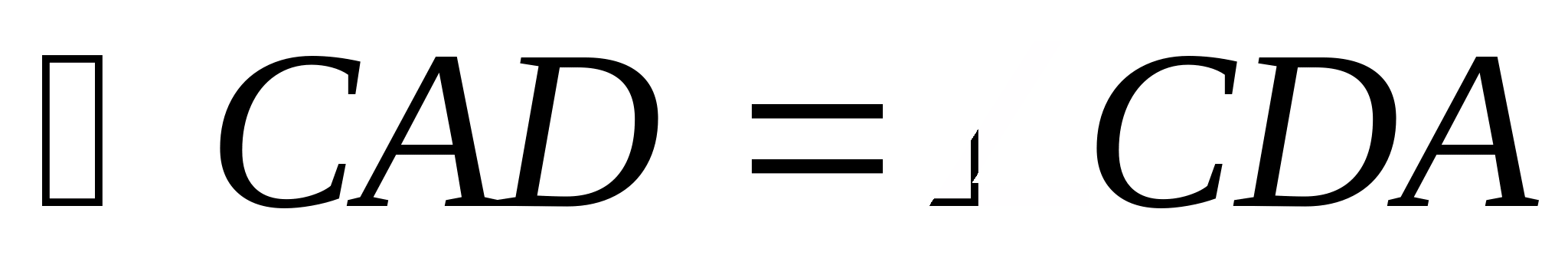 . В треугольнике ABD
угол A
DB
меньше угла BAD
, значит, BD
> AB
, или BC
+ CD
> AB
. Но CD
= AC
, значит, AC
+ BC
> AB
. Замечание
. Обратите внимание, что, исходя из формулировки теоремы, следует записать сразу три неравенства: AB
< AC
+ BC
; AC
< AB
+ BC
; BC
< AB
+ AC
. Нередко, записав одно неравенство, о двух других почему-то забывают. Помните, что это может привести к довольно неприятным ошибкам. Неравенство треугольника может служить одним из простых критериев принадлежности трех точек одной прямой
. Три точки будут принадлежать одной прямой тогда и только тогда, когда в неравенстве треугольника достигается равенство. Естественно, равенство может достигаться лишь в одном из трех неравенств (см. замечание), поскольку одна из точек будет лежать четко между двумя другими. Упражнение
. Докажите, что в треугольнике каждая сторона больше разности двух других сторон. Приведем в качестве примера использования неравенства треугольника несколько сравнительно несложных геометрических задач. Задача 1
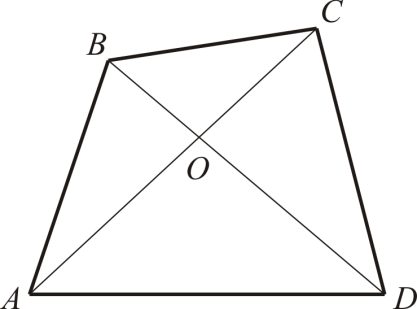
. Докажите, что в произвольном четырехугольнике ABCD
AB
+ CD
< AC
+ BD
.
. В треугольнике ABD
угол A
DB
меньше угла BAD
, значит, BD
> AB
, или BC
+ CD
> AB
. Но CD
= AC
, значит, AC
+ BC
> AB
. Замечание
. Обратите внимание, что, исходя из формулировки теоремы, следует записать сразу три неравенства: AB
< AC
+ BC
; AC
< AB
+ BC
; BC
< AB
+ AC
. Нередко, записав одно неравенство, о двух других почему-то забывают. Помните, что это может привести к довольно неприятным ошибкам. Неравенство треугольника может служить одним из простых критериев принадлежности трех точек одной прямой
. Три точки будут принадлежать одной прямой тогда и только тогда, когда в неравенстве треугольника достигается равенство. Естественно, равенство может достигаться лишь в одном из трех неравенств (см. замечание), поскольку одна из точек будет лежать четко между двумя другими. Упражнение
. Докажите, что в треугольнике каждая сторона больше разности двух других сторон. Приведем в качестве примера использования неравенства треугольника несколько сравнительно несложных геометрических задач. Задача 1
. Докажите, что в произвольном четырехугольнике ABCD
AB
+ CD
< AC
+ BD
. |
Евклид употребляет выраженияСначала определите две кратчайшие стороны: 3, и если вы найдете сумму двух кратчайших сторон, то она больше самой длинной? Сетевые координационные вложения, которые используют евклидовы расстояния, делают предположение о том, что неравенство треугольника в значительной степени не нарушается большой частью пар узлов. Неравенство треугольника утверждает, что для любого треугольника длина данной стороны должна быть меньше суммы двух других сторон, но больше разницы между двумя сторонами, т.е. стороны должны иметь возможность образовывать треугольник. |
AO + OB > AB ;
CO + OD > CD .
Рассмотрим сумму AC + BD :
AC + BD = (AO + OC ) + (BO + OD ) =
= (AO + BO ) + (OC + OD ) > AB + CD .
Задача 2 . Докажите, что в треугольнике ABC выполнено неравенство (a , b , c – стороны треугольника ABC ). Решение . Воспользуемся следствием из неравенства треугольника (см. упражнение): (предполагаем, что
(предполагаем, что 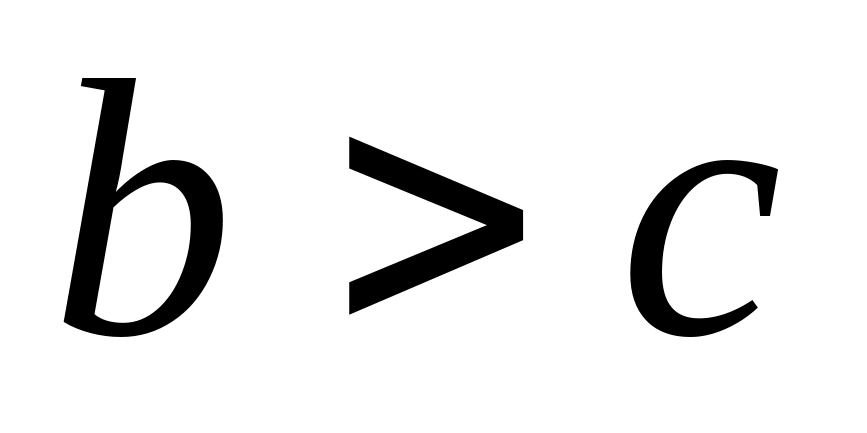 ). Тогда, возведя в квадрат обе части неравенства, получим:
). Тогда, возведя в квадрат обе части неравенства, получим: Аналогично:
Когда задержки между тройками узлов не могут образовать треугольник, говорят, что они нарушают неравенство треугольника. Узлы с большими и частыми нарушениями, как правило, с наибольшей индивидуальной ошибкой предсказания, и их существование снижает общую точность.
Мы используем метод от Тан и Кровели для изучения тяжести нарушений неравенства треугольника. Этот метод нормализует тяжесть каждого нарушения, позволяя сравнивать все пары. Для каждой пары узлов мы находим кратчайший путь между двумя, проходящими через третий узел.
На рисунке показано кумулятивное распределение этой величины, относительная длина пути. Мы обнаружили, что только несколько узлов являются членами многих из этих пар низких пар. Обратите внимание на изображение, когда наши сегменты линии имеют длины 3, 4 и 9 единиц, похоже, что у нас есть неполный треугольник. Похоже, что наши два линейных сегмента длиной 3 и 4 единицы слишком короткие или длина сегмента 9 слишком длинная. Но есть ли отношения между этими сегментами линий, которые должны быть истинными, верно?
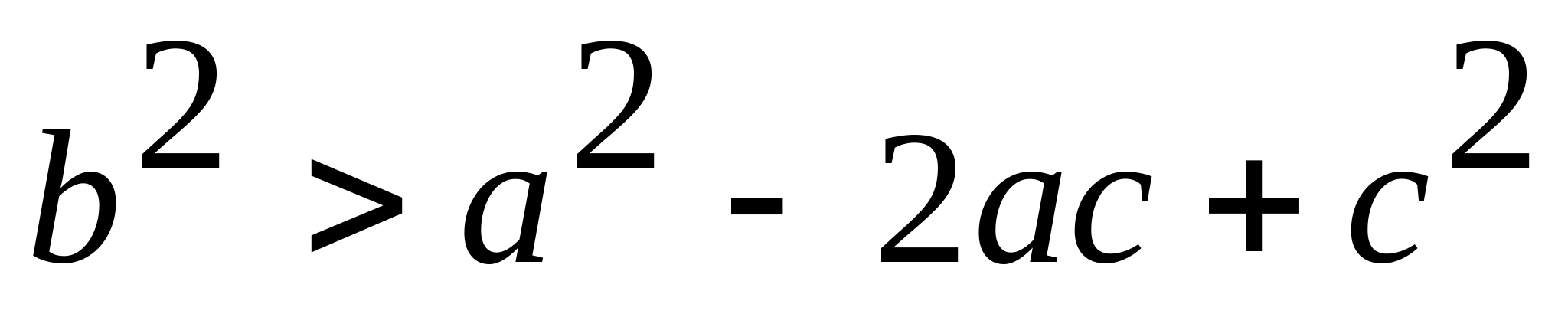 ;
;
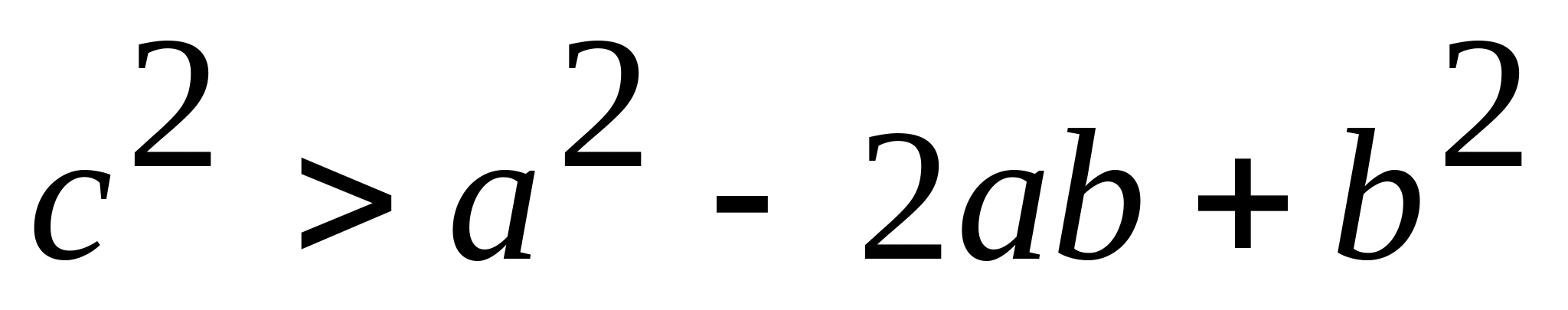 .
.
Складывая все три неравенства, получим требуемое. Упражнение
. Докажите, что медиана AM
в произвольном треугольнике ABC
по длине меньше, чем 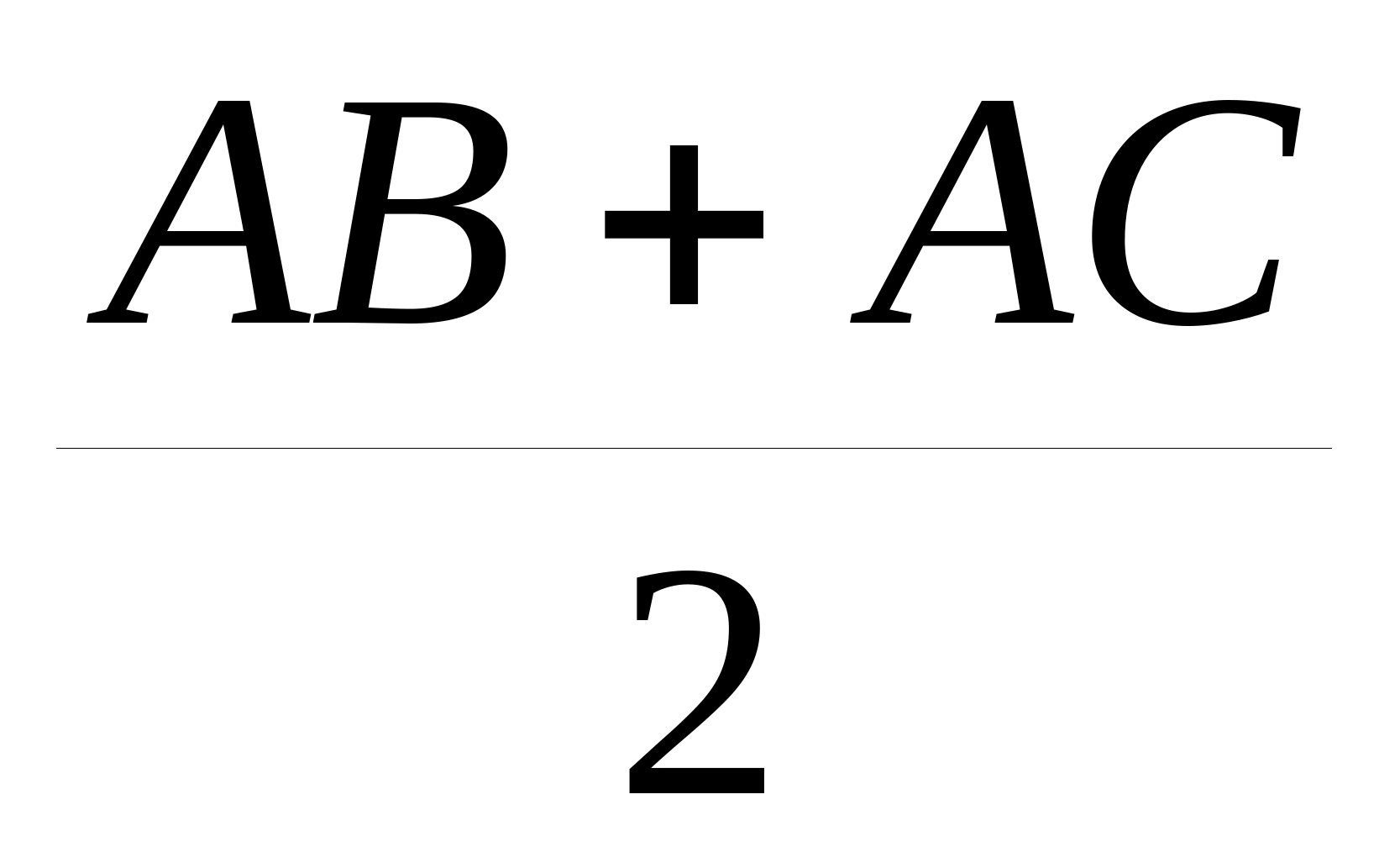 . Задача 3
. На плоскости дан квадрат ABCD
и точка O
. Докажите, что расстояние от точки O
до одной из вершин квадрата не превосходит суммы расстояний от O
до трех других вершин квадрата. Решение
. Сложите неравенства треугольника AC
+ OC
> OA
и OB
+ OD
> BD
. Так как AC
= BD
, то, сокращая, получаем требуемое. Задача 4
. Найдите внутри выпуклого четырехугольника точку, такую, что сумма расстояний от нее до вершин минимальна. Решение
. Так как четырехугольник выпуклый, то его диагонали пересекаются в точке O
внутри него. Обозначим вершины четырехугольника через A
, B
, C
и D
(по часовой стрелке). Тогда сумма расстояний от O
до вершин равна сумме длин диагоналей AC
и BD
. Но для любой другой точки P
имеем, во-первых, что сумма расстояний от P
до вершин не меньше AC
+ BD
, а во-вторых, либо PA
+ PC
> AC
, либо PB
+ PD
> BD
. Значит, эта сумма равна AC
+ BD
только если P
совпадает с точкой O
. Значит, точка O
– искомая. Неравенство треугольника успешно применяется и в довольно запутанных текстовых задачах. Что интересно, в таких задачах многое может зависеть от того, насколько удачно Вы построите геометрическую интерпретацию. Задача 5
. В некоторой стране расположены 4 города: A
, B
, C
и D
. Два самолета одновременно вылетели из города A
. Маршрут первого самолета: A
-B
-D
-C
-A
-D
-B
-C
-A
, а маршрут второго: A
-B
-C
-D
-A
-B
-C
-D
-A
-B
-C
-D
-A
. Какой из самолетов раньше закончит свой маршрут, если их скорости одинаковы? Не бойтесь экспериментировать! Если в задаче не задано конкретное расположение объектов, Вы вправе рисовать в своем решении всё, что не противоречит условию – оно ведь Ваше. В том числе, и города в Задаче 5 Вы можете расставить как угодно. Следует лишь помнить, что в некоторых задачах после разбора «нормального», общего случая, необходимо разобрать и некоторые «патологические», частные случаи. К примеру, в Задаче 5 может понадобиться рассмотрение случая, когда некоторые три города лежат на одной прямой – всё зависит от того, каково Ваше решение для общего случая. Решение задачи 5
. Запишем длины маршрутов каждого из самолетов в виде сумм расстояний между городами. Длина маршрута первого самолета будет равна
. Задача 3
. На плоскости дан квадрат ABCD
и точка O
. Докажите, что расстояние от точки O
до одной из вершин квадрата не превосходит суммы расстояний от O
до трех других вершин квадрата. Решение
. Сложите неравенства треугольника AC
+ OC
> OA
и OB
+ OD
> BD
. Так как AC
= BD
, то, сокращая, получаем требуемое. Задача 4
. Найдите внутри выпуклого четырехугольника точку, такую, что сумма расстояний от нее до вершин минимальна. Решение
. Так как четырехугольник выпуклый, то его диагонали пересекаются в точке O
внутри него. Обозначим вершины четырехугольника через A
, B
, C
и D
(по часовой стрелке). Тогда сумма расстояний от O
до вершин равна сумме длин диагоналей AC
и BD
. Но для любой другой точки P
имеем, во-первых, что сумма расстояний от P
до вершин не меньше AC
+ BD
, а во-вторых, либо PA
+ PC
> AC
, либо PB
+ PD
> BD
. Значит, эта сумма равна AC
+ BD
только если P
совпадает с точкой O
. Значит, точка O
– искомая. Неравенство треугольника успешно применяется и в довольно запутанных текстовых задачах. Что интересно, в таких задачах многое может зависеть от того, насколько удачно Вы построите геометрическую интерпретацию. Задача 5
. В некоторой стране расположены 4 города: A
, B
, C
и D
. Два самолета одновременно вылетели из города A
. Маршрут первого самолета: A
-B
-D
-C
-A
-D
-B
-C
-A
, а маршрут второго: A
-B
-C
-D
-A
-B
-C
-D
-A
-B
-C
-D
-A
. Какой из самолетов раньше закончит свой маршрут, если их скорости одинаковы? Не бойтесь экспериментировать! Если в задаче не задано конкретное расположение объектов, Вы вправе рисовать в своем решении всё, что не противоречит условию – оно ведь Ваше. В том числе, и города в Задаче 5 Вы можете расставить как угодно. Следует лишь помнить, что в некоторых задачах после разбора «нормального», общего случая, необходимо разобрать и некоторые «патологические», частные случаи. К примеру, в Задаче 5 может понадобиться рассмотрение случая, когда некоторые три города лежат на одной прямой – всё зависит от того, каково Ваше решение для общего случая. Решение задачи 5
. Запишем длины маршрутов каждого из самолетов в виде сумм расстояний между городами. Длина маршрута первого самолета будет равна
Как это бывает, существует и эта связь объясняется теоремой о неравенстве треугольника. Теорема о треугольном неравенстве утверждает, что длина любой из сторон треугольника должна быть короче, чем длины двух других сторон, сложенных вместе. Это говорит нам о том, что для того, чтобы три линейных сегмента создавали треугольник, должно быть верно, что ни одна из длин каждого из этих сегментов не превышает длину двух других сегментов линии.
Историческая справка о признаках равенства треугольников
Например, давайте посмотрим на наш первоначальный пример: нам удалось создать треугольник с линейными сегментами длиной 3, 4 и 5 единиц. Это связано с тем, что эти сегменты линии удовлетворяют теореме о неравенстве треугольника. Мы видим, что ни один из сегментов линии длиннее двух других сегментов линии.
Второй же самолет пролетит расстояние
Рассмотрим разность между расстоянием, которое пролетел первый самолет, и расстоянием, которое преодолел второй.
Докажем, что независимо от расположения точек A , B , C , D на плоскости (городов A , B , C , D в стране) выражение будет неположительным. Для этого следует рассмотреть два случая. 1. Предположим, что точки A , B , C , D ABCD с диагоналями AC и BD . Тогда запишем последовательно неравенства треугольника для треугольников ABC , BCD , CDA и DAB (см. рис. 2):
Однако, если мы рассмотрим линейные отрезки с длинами 3, 4 и 9, мы увидим, что сегмент линии с длиной 9 единиц длиннее двух других сегментов линии. Это объясняет, почему мы не могли создать треугольник с этими тремя отрезками линии. Они не удовлетворяют теореме о неравенстве треугольника.
Почему теорема о неравенстве треугольника верна?
Мы назовем это свойство кратчайшего расстояния, так как мы объясним, почему теорема о неравенстве треугольника верна. Вы можете использовать этот точный процесс, чтобы вывести, что это неравенство выполняется для каждой из сторон треугольника. Другими словами, это теорема о треугольном неравенстве: длина любой стороны треугольника должна быть короче, чем длины двух других сторон. Таким образом, мы показали, почему это неравенство верно!
AB + BC > AC ;
BC + CD > BD ;
CD + DA > CA ;
DA + AB > DB .
Сложив все четыре неравенства, получим
2. Рассмотрим случай, когда точки A , B , C , D создают на плоскости четырехугольник A C BD с диагоналями AB и CD (нарисуйте себе соответствующий рисунок). Заметим, что неравенства треугольника выполняются для тех же треугольников, что и в первом случае. Оказывается, что решение задачи останется тем же, несмотря на то, что расположение точек на плоскости существенно изменилось. Это можно считать еще одной характерной чертой многих решений задач, использующих неравенство треугольника. Следовательно, первый самолет прилетит раньше, поскольку его маршрут короче маршрута второго. Заметьте, что решение Задачи 5 требует небольшого анализа, что является непременным качеством всех олимпиадных задач. Будьте внимательны – Ваше решение задачи будет правильным лишь тогда, когда Вы рассмотрите все возможные случаи, подходящие под условие. Следует также отметить, что зачастую на рисунке, изображающем условие задачи, не видно треугольника, применение неравенства треугольника для которого дало бы моментальное решение. В таком случае может помочь удачно подобранное геометрическое преобразование. Об этом мы поговорим несколько позже. Знакомство с неравенством треугольника на этом следует объявить законченным. Но новая встреча с ним уже не за горами. 7 класс Лекция 13. Неравенство треугольника
Чтобы дать вам быстрый пересмотр, теорема о неравенстве треугольника утверждает, что длина любой из сторон треугольника должна быть короче, чем длины двух других двух сторон. Мы теперь видели, как использовать это неравенство, чтобы определить, могут ли три отрезка линии сформировать треугольник. Мы только что определили, что ни один из сегментов линии не длиннее, чем два других вместе взятых. Если это так, то сегменты линии могут формироваться треугольник. Мы также видели, почему неравенство треугольника истинно; это делает нас чрезвычайно удобными в работе с ним и применении его к приложениям.
Фихте Иоганн Готлиб (1762-1814) один из виднейших представителей классической немецкой философии. Вкнигу вошли известные работы: «Факты сознания», «Назначение человека», «Наукоучение» идругие книга
КнигаФихте Иоганн Готлиб (1762-1814) - один из виднейших представителей классической немецкой философии. В книгу вошли известные работы: «Факты сознания», «Назначение человека», «Наукоучение» и другие.
Постановка домашнего задания
Треугольник не может быть построен из любых трех случайных отрезков. Попытка сделать это может привести к созданию вырожденного треугольника, треугольника, который не может соединить все его стороны. Чтобы гарантировать, что мы получим законный треугольник, мы используем нечто, известное как неравенство треугольника, которое связывает три стороны треугольника.
Если \\, \\, \\ - длины трех сторон треугольника, то. Если какое-либо из этих неравенств неверно, то получим вырожденный треугольник. Мы покажем основные расчеты с использованием этих формул, включая определение того, является ли треугольник вырожденным.
Жозеф Артур Гобино. Опыт о неравенстве человеческих рас книга
КнигаКаким бы зловещим не представлялся в СМИ и литературе нынешнему и прошлому поколениям национал-социализм, он не перестает привлекать к себе внимания миллионов людей.
Пентаграмма является одним из важнейших магических символов. Само это слово происходит от греческих слов "pente", что означает пять, и "gramma" буква
ДокументСимвол защиты и власти - ПентаграммаMarsyas Пентаграмма является одним из важнейших магических символов. Само это слово происходит от греческих слов "pente", что означает пять, и "gramma" - буква; пентаграмма -
Определение вырожденных треугольников
Здесь будут указаны все три длины сторон треугольника, и вы должны определить, является ли треугольник вырожденным. Пример 1: Треугольник со сторонами длин \\, \\ и \\ - вырожденный треугольник? Решение: Пусть \\, \\ и \\. Чтобы убедиться, что это не вырожденный треугольник, мы должны подключить эти длины сторон ко всем трем частям неравенства треугольника.
Все три из этих неравенств верны, поэтому это не вырожденный треугольник. Пример 2: Треугольник со сторонами длин \\, \\ и \\ вырожден? Решение. Одна сторона длиннее двух других. Поэтому возникает вырожденный треугольник. Все три неравенства должны быть истинными, и только два из них.
Видеоурок «Неравенство треугольника» раскрывает содержание и доказательство теоремы о неравенстве треугольника. Задача данного видеоурока - облегчить запоминание теоремы и следствия из нее, понимание и запоминание хода рассуждений при ее доказательстве.
Высокий уровень наглядности материала, голосовое сопровождение дает возможность использовать данное пособие в качестве самостоятельной части урока, освобождая время учителя для улучшения качества обучения, усиления индивидуальной работы с учениками.
Создание невырожденных треугольников
Пример 3. Делают ли боковые длины \\, \\ и \\ производят вырожденный треугольник? Здесь обратите внимание, что одна сторона точно так же, как две другие вместе, так что \\, и это неверно, что \\, что нарушает неравенство треугольника, поэтому этот треугольник является вырожденным. В этом разделе статьи мы будем использовать примеры, чтобы проиллюстрировать, как построить треугольники, чтобы они не вырождались.
Пример 4. Две стороны треугольника имеют длины \\ и \\. Каков диапазон возможных длин для третьей стороны? Пусть \\ - сторона с неизвестной длиной. Тогда все три неравенства должны выполняться неравенством треугольника. Изолируйте \\ в каждом неравенстве и максимально упростите.
Видеоурок начинается с представления темы и формулировки теоремы о неравенстве треугольника. Для запоминания утверждения теоремы она выведена на экран и выделена цветом. Данная теорема утверждает, что любая сторона треугольника является меньшей суммы двух других его сторон. Доказательство утверждения предлагается рассмотреть на примере треугольника Δ, демонстрируемого под текстом теоремы на экране.
Из этих ограничений мы знаем, что \\ больше \\, но меньше \\. Пример 5: Треугольники равностороннего треугольника, где все три стороны имеют одинаковую длину. Докажите, что эти треугольники не вырождены. Пусть длина стороны всех трех треугольников равна.
Затем, по неравенству треугольника, мы вставляем длины сторон в три условия формулы. Так как \\ должно быть положительным, это неравенство верно. В результате равносторонний треугольник никогда не будет вырожден. Пример 6: равнобедренный треугольник имеет две стороны одинаковой длины. Докажите, что третья сторона менее чем вдвое длиннее любой из сторон одной длины.
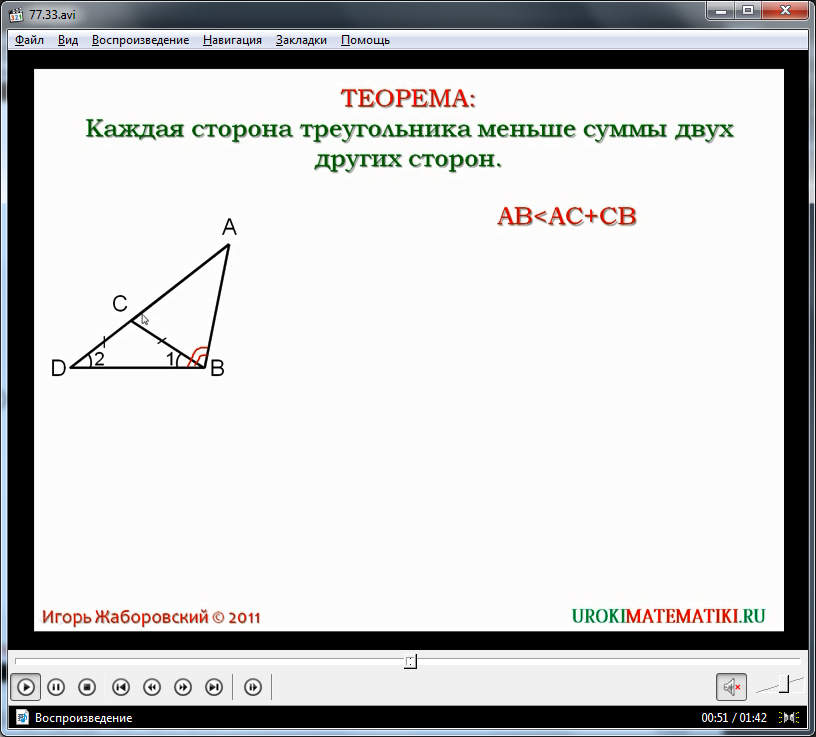
Уточняется, что для доказательства теоремы необходимо подтвердить, что сторона AB является меньше величины суммы сторон AC и CB. Данное утверждения обозначено на экране выражением AB Пусть длина стороны одной из равнобедренных сторон равна \\. Пусть длина стороны третьей стороны равна \\. Тогда по неравенству треугольника. Это неравенство гласит, что объединенная длина двух сторон одинаковой длины длиннее длины другой стороны, именно то, что мы хотели доказать. Неравенство Треугольника - это простое понятие, которое связывает стороны треугольника. Он служит надежной проверкой того, что вы не создали вырожденный треугольник, и это фундаментальный закон в основе геометрии. Социальное неравенство вызвано концентрацией доходов и контрастом великих бразильских городов. Это темы, затронутые в социологическом классе Проекта образования в эту пятницу. Освоив данную теорему, можно рассматривать ее следствие, утверждающее, что для любых трех точек A,B,C, которые не принадлежат одной прямой, справедливы неравенства: AB С одной стороны комфортное проживание в роскошных апартаментах благородных районов города. С другой стороны, бедность, трудная жизнь тех, кто нуждается в выживании в страданиях, часто без основной гигиены, без доступа к образованию, культуре и досугу. Именно неравенство все чаще присутствует в обществе. Когда они сталкиваются с реальностью, как тот, кто имеет гуманистическое видение чувствует себя очень шокированы, тронутым, потому что это то, что не допускается в гуманистическом сознании состояния человеческой жизни перед лицом столь значительного прогресса, так много технологий, поэтому доступ сегодня товары и услуги, которые каждый может иметь, и мы сталкиваемся с таким очевидным неравенством, - комментирует профессор социологии Фабио Медейрос. Видеоурок «Неравенство треугольника» может быть использовано учителем на уроке геометрии в качестве наглядного пособия или как часть урока вместо объяснения учителем новой темы. Подробное понятное объяснение заменит учителя при самостоятельном изучении предмета учеником, а также поможет объяснить предмет при дистанционном обучении.Жозеф Артур Гобино. Опыт о неравенстве человеческих рас книга

![]()
- Манная каша на молоке: пропорции и рецепты приготовления Манная каша 1 порция
- Суп-пюре из брокколи с сыром Рецепт крем супа из брокколи с сыром
- Гороскоп: характеристика Девы, рождённой в год Петуха
- Причины выброса токсичных веществ Несгораемые углеводороды и сажа
- Современный этап развития человечества
- Лилия яковлевна амарфий Могила лилии амарфий
- Значение имени мариям Имя марьям значение происхождение

 Live Journal
Live Journal Facebook
Facebook Twitter
Twitter